Diffraction (physics)

If the hole diameter is significantly smaller than the wavelength, spherical waves are created behind it.

The diffraction or diffraction is the distraction of waves on an obstacle. A wave can propagate through diffraction in areas of space that would be blocked on a straight path by the obstacle. Any kind of physical wave can show diffraction. It is particularly noticeable with water waves or with sound . With light , diffraction is a factor that limits the resolution of camera lenses and telescopes . Some technical components, such as diffraction gratings , make targeted use of diffraction.

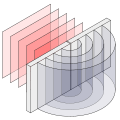
Diffraction occurs through the creation of new waves along a wave front according to the Huygens-Fresnel principle . These can lead to interference phenomena through overlay .

In contrast to the diffraction takes place at the scattering a deflection of radiation by interaction of particles instead. In the case of coherent , coherent scattering, one also speaks of reflection .
In the case of refraction , the deflection of radiation is based on the change in the speed of propagation with a change in the density or the composition of the propagation medium , most clearly when passing through a phase boundary .

history

Christiaan Huygens noticed as early as 1650 that certain previously inexplicable phenomena can be described with the propagation of light in wave form. He formulated the Huygens principle and thus founded wave optics . The effect of the diffraction of light at an optical slit was finally observed in 1662 by Francesco Maria Grimaldi , who described light as a wave in his work De lumine . In 1802 Thomas Young carried out corresponding experiments on the double slit . A complete physical description of diffraction could be provided by Augustin Jean Fresnel in 1818 , which was initially questioned by Siméon Denis Poisson , but shortly afterwards by François Arago through the experimental proof of the Poisson spots theoretically predicted by Poisson himself during diffraction on one Ball could be confirmed.

In 1835 Friedrich Magnus Schwerd investigated diffraction phenomena on regular gratings, which could also be described with the help of wave optics. In 1909, Geoffrey Ingram Taylor was able to show in the Taylor experiment that light with extremely low intensity, i.e. also individual photons, is diffracted, with which the wave-particle dualism could be demonstrated.

In 1924 Louis-Victor de Broglie developed the theory of matter waves , and just three years later Clinton Joseph Davisson and George Paget Thomson were able to show through experiments on electron diffraction that particles with mass can also be bent. Another three years later, Otto Stern , Otto Robert Frisch and Immanuel Estermann were able to demonstrate this effect by diffracting rays from helium atoms and hydrogen molecules on a lithium fluoride crystal . In 1961, Claus Jönsson also carried out experiments on the diffraction of electrons at single and double slits .

Diffraction at diaphragms

Diffraction at a single slit with slit width s and deflection angle φ : The picture illustrates the attenuation of the radiation at the first minimum. For illustration, the beam is divided into two halves, so that a beam from the lower half with the path difference d can be assigned to each individual beam from the upper half . If d is equal to half the wavelength λ, there is an intensity minimum, since a wave crest of a single beam in the upper half is superimposed by a wave trough of a beam in the lower half. For the following orders of the minima, the ray is divided into four, six, etc. parts.

Because of the wave nature of the light , its real behavior deviates strongly from what the geometric optics would suggest. In photography, for example, the resolution of a photo is limited by the diameter ( aperture ) of the lens due to diffraction .

The physical model for diffraction is the Huygens-Fresnel principle . For the calculation of diffraction patterns is Kirchhoff diffraction integral used, the two limiting cases the Fresnel diffraction (diverging point source of radiation) and the Fraunhofer diffraction are (parallel light rays as the radiation source). The superposition of the elementary waves can lead to mutual reinforcement (constructive interference ) or mutual weakening (destructive interference) or even cancellation, see also path difference .

Slit and intensity distribution of monochromatic light behind the slit as an image and curve for a narrow (above) or wide slit. The diffraction phenomena are clearly recognizable with a narrow slit, minima and maxima occur, wavelength and slit width are of the same order of magnitude.

Diffraction can be observed well, among other things, if geometric structures play a role, the size of which is comparable to the wavelength of the waves used. Optical diaphragms are dimensioned depending on the application in such a way that they cause diffraction effects - i.e. with dimensions in the range and below the light wavelength, or with sufficient accuracy none - then with dimensions well above the light wavelength.

Examples of diffraction at diaphragms

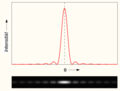
Diffraction at a single slit : If you mentally divide a light bundle that is deflected in a certain direction at a single slit into two halves, these two parts of the light bundle can constructively or destructively overlap. A series of diffraction maxima thus results again at a slit.

If the slot width is significantly smaller than the wavelength, cylindrical waves are created behind it.
Diffraction at a single slit
Diffraction at a single slit - light with a longer wavelength (green) is more strongly diffracted, the diffraction pattern is fanned out further
Diffraction at a single slit - light with a shorter wavelength (blue) is diffracted less strongly with the same slit width, the diffraction pattern is narrower
Diffraction of the sun's light at a circular pinhole - the shorter the wavelength, the less the corresponding color components are diffracted

Diffraction patterns that differ greatly in some cases occur on diaphragms of other shapes.

Diffraction at a circular opening
Diffraction at a rectangular opening

Diffraction at the grating

Diffraction of a laser beam on an optical grating

Diffraction at the grating (g = grating constant, φ = deflection angle, d = path difference)

Grids are diaphragms with periodic columns. Diffraction at the grating is therefore an important special case of diffraction at diaphragms.

Optical grating: If many gaps are arranged at regular intervals, a series of diffraction reflections results, the arrangement of which corresponds to that which one would expect with a double gap with the same distance. However, as the number of individual columns increases, the reflections become increasingly sharp lines. Since the position of the reflections depends on the wavelength of the light, optical grids can be used to separate different wavelengths. This is the case in the monochromator and in spectroscopy . In practice, regular arrangements of reflective and non-reflective strips are very often used as reflection gratings. The unprinted side of a CD looks similar.

Diffraction on the crystal lattice, Bragg equation

X-ray diffraction: This is used in crystallography to determine and measure crystal lattices . The wavelength of the X-rays is comparable to the lattice spacing in the crystal, and the crystal lattice acts as a multi-dimensional optical lattice.

Other types of waves

In principle, laws that apply to the diffraction of light waves also apply to other wave phenomena.

In acoustics : The diffraction of sound is important for calculating the shielding effect of noise barriers .

In particle physics one deals inter alia with the electron diffraction .

With directional radio , the diffraction at obstacles in the propagation path plays a role in damping or amplifying the signal, see Fresnel zone .

Water waves : In the water there are interesting superimpositions of waves ( quay walls , motor boats, etc.), and monster waves can form due to superposition effects . Similar effects can be used to locate submarines, schools of fish and the like. a. use underwater.

In quantum mechanics , every particle also has wave properties, so diffraction of particle beams is possible, even if it is difficult to access experimentally. It could e.g. B. the diffraction of rays from C ₆₀ molecules can be demonstrated in experiments.

Diffraction of helium atoms as an investigation method in surface physics ( helium atom beam scattering ).

Web links

Commons : Diffraction (physics) - album of pictures, videos and audio files

References and comments

^ F. Dorn, F. Bader: Physics upper level. Schroedel, Hannover 1986, ISBN 3-507-86205-0 .
↑ Both in the Fresnel diffraction and Fraunhofer diffraction when it is related to. The Maxwell equations for the far field approximations , because the distance between the diffraction elements i of the light source in both cases. a. is much larger than the wavelength of light .
↑ Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger: Wave-particle duality of C60 molecules . In: Nature . tape 401 , no. 6754 , September 14, 1999, p. 680-682 , doi : 10.1038 / 44348 .

[1] F. Dorn, F. Bader: Physics upper level. Schroedel, Hannover 1986, ISBN 3-507-86205-0 .

[2] Both in the Fresnel diffraction and Fraunhofer diffraction when it is related to. The Maxwell equations for the far field approximations , because the distance between the diffraction elements i of the light source in both cases. a. is much larger than the wavelength of light .

[3] Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger: Wave-particle duality of C60 molecules . In: Nature . tape 401 , no. 6754 , September 14, 1999, p. 680-682 , doi : 10.1038 / 44348 .