Optical gap

Typical design of a rectangular optical gap (slit diaphragm) with edges that can be adjusted via four screws (in x and y directions) for optical laboratory setups

In optics, an optical slit or slit diaphragm is a diaphragm with a narrow, elongated, usually rectangular opening. Slit diaphragms are often used to select the desired light spectral components, to block out unwanted light or to shape beams.

technical structure

Slit diaphragms are implemented as a light passage in a flat carrier. In the past, a glass plate blackened with soot (possibly in a slide frame ) was used in the laboratory , on which the blackening was removed in the desired shape (line, rectangle, ...) with a pointed object ( scalpel , knife). Today the screen is usually made of metal plates, which are often thinned in a wedge shape towards the gap (such as the cutting edge of scissors), as an adjustable air gap (see picture above). In order to avoid reflections on the edges of the diaphragm and to enable a well-defined position of the slit diaphragm in the room, the diaphragm leaves are usually designed as thin sheets (a maximum of a few millimeters thick).

In order to avoid stray light and glare, the non-translucent parts are usually kept matt black, sometimes roughened.

A second pair of metal plates can often also be used to adjust the height of the gap opening. As with the gap width, this is usually done by hand using adjusting screws, as this is adjusted at most once per series of measurements. Continuous adjustment that would require a servo drive rarely occurs.

Intensity distribution behind slit diaphragms

General

Intensity distribution behind a narrow (above) and wide (below) slit, when illuminated with a laser . The slit can be seen on the left, a photo in the middle and the vertically summed up intensity distribution on the right.

If a slit diaphragm is used to shape the beam and its opening is completely illuminated with coherent light , diffraction effects can play an important role. In order to describe these effects, the light must be viewed in the context of wave optics . The strength and visibility of these effects depends essentially on the Fresnel number , which describes the ratio of the width of the slit , the wavelength of the incident light and the distance between the observer and the slit: ${\displaystyle N_{\text{F}}}$ ${\displaystyle D}$ ${\displaystyle \lambda }$ ${\displaystyle d}$

${\displaystyle N_{\text{F}}={\frac {(D/2)^{2}}{\lambda \cdot d}}}$

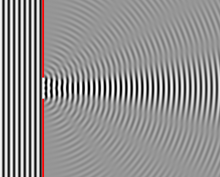
The intensity distribution can be calculated with the diffraction integral. It is assumed that a spherical wave propagates from every point of the gap. The diffraction integral then calculates the sum over all these spherical waves. The following figure shows (numerical) results for different distances (Fresnel numbers ) of the observer from the slit: ${\displaystyle d}$ ${\displaystyle N_{\text{F}}}$

• 

  Fig. 1: Field distribution in the near field and far field of an optical slit that is illuminated by a plane wave.

The Babinet principle also applies to the diffraction phenomena at the optical slit , so the resulting diffraction pattern is the same as that of a straight wire.

Near field

Near-field diffraction image of a single slit

For large Fresnel numbers, the intensity distribution shows the slit shape indicated in dark gray well. The fluctuations on the plateau of the intensity distribution result from the diffraction at the slit edges. In this regime ( geometric optics ) diffraction effects are mostly negligible. Depending on the width of the gap, this regime can also occur at a great distance from the gap. So is z. B. with a green light ( ) for a wide gap still given for the distance . ${\displaystyle \lambda =500\;\mathrm {nm} }$ ${\displaystyle D=10\;\mathrm {mm} }$ ${\displaystyle N_{\text{F}}>10}$ ${\displaystyle d=5\;\mathrm {m} }$

Far field

Fig. 2: Diffraction image in the far field of a rectangular diaphragm (shown enlarged above)

Fig. 3: Far-field diffraction image of a single slit with explanations for deriving the diffraction minima and maxima

Fig. 4: Wavefronts behind an opening that is four times as wide as the wavelength. Gray means zero amplitude.

For narrow slits with a slit width D close to the wavelength (e.g. D = 10 · λ = 5 µm), on the other hand, the far field image (here ) is already very close behind the slit (in the example about d = 1.25 mm) , and in practice only this is observed. The most striking property of this far field is its strong broadening compared to the gap width, which is indicated in Figure 1 above by the two differently scaled graphs for . The diffraction image in the far field is calculated using the Fraunhofer approximation for the diffraction integral (see there). This gives the diffraction image as a Fourier transform of the shape of the aperture. An example is shown on the right. ${\displaystyle N_{\text{F}}<0{,}01}$ ${\displaystyle N_{\text{F}}=0{,}025}$

It is often sufficient to limit the observation to a plane parallel to the direction of propagation of the light. Then you can calculate the image that an observer can see behind the gap. If you look at this at the angle to the optical axis (see Figure 3 right), you get: ${\displaystyle \varphi }$

${\displaystyle I(\varphi )\propto \left({\frac {\sin(\pi D\cdot \sin(\varphi )/\lambda )}{\pi D\cdot \sin(\varphi )/\lambda }}\right)^{2}=\operatorname {si} ^{2}\left({\frac {\pi D\cdot \sin(\varphi )}{\lambda }}\right)=\operatorname {sinc} ^{2}\left({\frac {D\cdot \sin(\varphi )}{\lambda }}\right)}$

For small distances from the optical axis, the distribution of the intensity along an axis parallel to the slit plane can be given approximately: ${\displaystyle x=d\cdot \tan \varphi }$

${\displaystyle I(x)\propto \left({\frac {\sin(\pi Dx/(\lambda d))}{\pi Dx/(\lambda d)}}\right)^{2}=\operatorname {si} ^{2}\left({\frac {\pi Dx}{\lambda d}}\right)=\operatorname {sinc} ^{2}\left({\frac {Dx}{\lambda d}}\right)}$

This distribution is also known as the split function (see also sinc function si ( x ) or sinc ( x ) ) and is shown in the upper part of Figure 3 on the right. Some properties (minima) of this one-dimensional intensity distribution can also be clearly derived. They are of great importance for quick estimates (the distance between the two minima close to can be used as a measure of the size of the diffraction pattern) and as instructive application of the principles of diffraction at an aperture: ${\displaystyle \varphi =0}$

To do this, one follows the Huygens principle and assumes that a spherical wave emanates from every point on the diaphragm . These waves propagate independently and interfere with the observer. The observer can now see the gap at an angle φ (see lower part of Figure 3 on the right). If the path difference 2s (see lower part of Figure 3 right) between the rays from the slit edges is just the wavelength λ , the ray can be divided into two partial bundles. For each partial ray of the first bundle there is always exactly one partial ray in the second bundle, with a relative path difference of λ / 2 . These two partial beams thus interfere destructively and cancel each other out. This extinguishes the entire intensity and we observe an intensity minimum. The same reasoning applies if the path difference between the outer rays is an integral multiple nλ of the wavelength; one then only divides into correspondingly more sub-bundles n . Then there is also a partner with a path difference of λ / 2 for every ray in every partial bundle . This cancellation condition reads (with the path difference s ):

${\displaystyle \sin \varphi _{\mathrm {min} ,n}={\frac {2s}{D}}=\pm n\cdot {\frac {\lambda }{D}},\quad n\in \mathbb {N} }$

One speaks in each case of the minimum of the nth order.

There is no simple derivation for the maxima. They can be calculated using the extremes of the sinc function, which are detailed in the article on the sinc function .

The intensity of these maxima drops rapidly for large angles. The maximum of the zeroth order can be found at φ = 0, i.e. on the optical axis.

In particular, the condition for the minima can be used to estimate the broadening of the intensity distribution behind a slit. As already shown above, the far field distribution is much wider than the gap itself. The opening angle can be defined as and results e.g. B. for a gap with a width of 10 wavelengths ( D = 10λ , e.g. 5 μm for green light) to about α = 11.5 °. The light beam widens very quickly behind the gap. For a slit of 1000 wavelengths (e.g. 0.5 mm for green light), on the other hand, the result is only α = 0.1 ° and the slit must be observed at a very large distance in order to observe a noticeable broadening. ${\displaystyle \alpha :=2\varphi _{\mathrm {min} ,1}}$

With the help of these formulas z. B. the wavelength of the incident light on a known slit can be measured by measuring the angular spacing of the minima of the nth order. Conversely, if the wavelength is known, conclusions can also be drawn about the width of the gap.

Wide and narrow gaps

The division, which is often made solely on the basis of the ratio of the slit width to the wavelength λ, into wide slits (in which the near field dominates, so diffraction phenomena can be neglected) and narrow slits (in which the far field dominates) must be handled carefully. As shown above, this distinction does not depend on the width of the gap, but on the number of Fresnel . ${\displaystyle D}$ ${\displaystyle N_{\text{F}}}$

In practice, however, this inaccuracy rarely leads to problems, since almost only the near field is observed at a wide gap, while the far field can only be seen at a large distance from the gap. On the other hand, in a narrow gap, the near field can only be seen at an extraordinarily small distance from the gap; in practice, the far field is usually observed.

Polarization effect

Since the jaws of the gap are mostly made of metal, this can additionally influence the light passing through. The conductive metal short-circuits an electric field parallel to its surface and thereby attenuates this component of the light. The component of the light that is polarized perpendicular to the metal surface is practically unaffected. Partial polarization is therefore carried out with a preference for the E-field component across the gap. However, this is a small effect that decreases sharply as the gap width increases and is of no practical use. In the case of precision measurements, it may have to be included in the consideration.

application

Monochromators and spectrometers

Wavelength selection through a slit diaphragm in a monochromator : incident light A is  split into the spectral colors by a grating D ( dispersion ). The grating D is rotated so that only light of the desired color passes through the exit slit F.

In physics, slit diaphragms are mainly used in spectrometers and monochromators . There they are used to select a part of the previously split light spectrum (see figure on the right). A dispersive element, such as a diffraction grating or a prism , is first used to spectrally split incident light. A spectral range of the light is then selected by masking out the other ranges through a slit diaphragm. In monochromators, light can be generated from a selectable and defined spectral range. In spectrometers, a certain wavelength is selected with which the following measurement is carried out. By moving the slit or, better still, rotating the dispersive element, the entire spectrum can then be gradually recorded. In the optical test apparatus, the slit diaphragm also serves as a secondary light source for the further beam path .

The slit diaphragm is also used as a secondary light source directly in front of the dispersive element in order to ensure a defined arrangement and shape of the light source on its entrance side. For this purpose, the diaphragm is irradiated by a broadband (white) light source, which is roughly focused on the gap, for example by means of concave mirror optics.

When used as a beam limiter, however, diffraction effects at the gap would interfere. Therefore, one always chooses the gap width sufficiently large so that diffraction effects are not relevant. This in turn limits the achievable wavelength resolution, which is why an optimal intermediate value should be aimed for.

Beam shaping

Slit diaphragms can also be used more generally for beam shaping. They are illuminated over a large area from behind and form a rectangular beam of adjustable dimensions. This can prevent light from falling on parts of an optical structure in which it would interfere with scattering or unwanted reflections. This principle finds z. B. in light disk microscopy (SPIM) application. Here an adjustable slit forms a rectangular beam, which is then focused into a sheet of light with the help of a cylindrical lens. It is even easier to use in the slit ultrasonic microscope , in which an illuminated optical slit is imaged in a sample with a simple condenser lens. Particles that pass through the light sheet formed in this way can be detected by their scattered light.

The width of such panels can often be adjusted by hand. In the case of monochromator applications, the width is adapted to the wavelength range used or to the required intensity (resolution is sacrificed, for example, by a wider setting in order to achieve more intensity and thus a better signal-to-noise ratio ). The height of the gap used is often adjustable, again to ensure defined conditions for the beam.

When the beam is formed, gaps are usually so wide that a single-gap diffraction pattern cannot be seen. Diffraction can still be seen at the edges of the slit, which leads to a widened drop in the edge intensities (see picture of the wide slit, top).

Field of view limitation

Conversely, apertures are also often used to delimit image fields. For example, a small area can be cut out of a microscope image and then only displayed on part of an image sensor. With the help of additional optics, the same image section can then be displayed again, slightly offset. If both sections are sent through different optical filters , you can record the same section simultaneously in several spectral ranges without having to use several cameras.

Phototechnology

Vertically moved focal plane shutter with an exposure time of 1 / 500s - below you can clearly see the gap between the aperture leaves.

Cameras have wide slit diaphragms with a greater spacing (approx. 0.8 - 1.0 mm) in panorama cameras and in technical applications. They can also be seen here as a transition to the electronic line scan camera . A slit-shaped section is exposed in the same way as the focal plane shutter , but the film (or film section is moved by the movement of the lens) during the exposure.

Individual evidence

1. ^ Bahaa EA Saleh, Malvin Carl Teich: Fundamentals of photonics . Wiley-Interscience, February 22, 2007, ISBN 978-0-471-35832-9 , pp. 132-133.
2. ↑ mike-willis.com: Diffraction
3. ↑ Wolfgang Demtröder : Experimentalphysik 2. Electricity and optics . Springer Verlag , 2006, ISBN 3-540-33794-6 , pp. 322-324.
4. ^ Christian Gerthsen: Gerthsen Physics . Springer Verlag , August 19, 2003, ISBN 978-3-540-02622-8 , pp. 523-524 (accessed on August 13, 2011).
5. ↑ Wolfgang Demtröder: Laser spectroscopy: Basics and techniques . Springer, August 1, 2007, ISBN 978-3-540-33792-8 , pp. 68-69 (accessed August 13, 2011).
6. ↑ K. Greger, J. Swoger, EH Stelzer: Basic building units and properties of a fluorescence single plane illumination microscope. In: The Review of scientific instruments Volume 78, Number 2, February 2007, P. 023705, ISSN  0034-6748 . PMID 17578115 .
7. ^ Nobel Prize lecture by RA Zsigmondy (English): Properties of colloids (PDF; 108 kB), with an illustration and a brief explanation of the ultramicroscope
8. ↑ K. Kinosita, H. Itoh, S. Ishiwata, K. Hirano, T. Nishizaka, T. Hayakawa: Dual-view microscopy with a single camera: real-time imaging of molecular orientations and calcium. In: Journal of Cell Biology Volume 115, Number 1, October 1991, pp. 67-73, ISSN  0021-9525 . PMID 1918140 . PMC 228992 (free full text).