Huygens principle
The Huygens principle or Huygens principle , also called the Huygens -Fresnel principle (after Christiaan Huygens and Augustin Jean Fresnel ), states that every point of a wave front can be viewed as the starting point of a new wave , the so-called elementary wave . The new position of the wavefront is obtained by superposition ( superposition ) of all elementary waves. Since the elementary wave has a spherical or circular shape, a returning wave is also formed. Many special cases follow from the Huygens principle, such as diffraction phenomena in the far field ( Fraunhofer diffraction) or near field diffraction ( Fresnel diffraction ).
Huygens principle in physics

The concept was proposed by Christiaan Huygens in 1678 to explain the propagation of light . Accordingly, every point that is reached by a wave front is the starting point for a spherical or circular elementary wave , which propagates in the same propagation medium at the same speed as the original wave. The wavefront that spreads further results as the outer envelope of the elementary waves . Huygens assumed that the elementary waves do not work backwards, but only in the direction of propagation , but could not give a qualitative explanation for this.
At the boundary between two media in which the waves have a different speed of propagation, a wave front that does not hit perpendicularly changes its direction. Huygens' theory thus offered a simpler explanation for the reflection and refraction of light than was possible with Newton's corpuscle theory .

In 1816, Augustin Fresnel was able to expand this principle and thus explain the diffraction of light on obstacles. He showed that according to the principle of interference, the resulting wave can be calculated by superposing all elementary waves. Among other things, Poisson predicted that if light was diffracted by a round object, a Poisson spot would be created. The experimental confirmation of this phenomenon was a victory of wave optics over the corpuscle theory widespread at the time. Gustav Kirchhoff then showed how the Huygens principle can be derived from the Maxwell equations and presented the more precise solution in the form of the Kirchhoff diffraction integral .
Huygens postulated the ether as the medium of propagation of the light waves . Since the general acceptance of Albert Einstein's special theory of relativity published in 1905, this is no longer required as a physical concept. The apparent contradiction between the particle and wave character of light is resolved in quantum mechanics . In this context, the Huygens principle in the form of the pointer model is used to clearly explain the propagation of probability waves.
Huygens' principle in mathematics
In mathematics, Huygens' principle is used in the theory of partial differential equations. It says that wave equations have a back wave front in the spaces for . One speaks of the existence of a rear wave front if a disturbance of the output data in the vicinity of a point does not affect the solution of the wave equation for sufficiently long times t.
Explanation of the Huygens principle using the simple wave equation
The starting dates (for ) are:
with as a time variable and as a location variable.
The case n = 1
According to d'Alembert's formula, the following applies to :
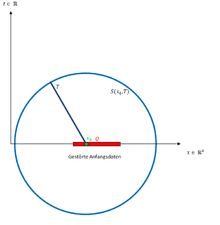
If we disturb the start date in the interval , the above formula shows that the disturbance at the point in time no longer has any influence on the point , because the start dates and were not disturbed. The Huygens principle applies to.
Be and one disturb the start date in . Then you will find that for every point in time T the disturbance still has an impact on the solutions , because you integrate over the "disturbance interval":
Conclusion: In the one-dimensional, the Huygens principle does not generally apply, but only applies to the start date .
The case n = 2
The general solution formula for the two-dimensional case (using the descent method) is:
denotes the (filled) circular disc with center and radius .
From this formula you can see immediately that the Huygens principle does not apply. Because if you disturb the initial data or in a rectangle , the disturbance also affects all points at any point in time , because the circular disk contains the rectangle R for these points . So it is integrated again over disturbed data.
The case n = 3
According to Kirchhoff's formula, the solution to the wave equation is:
denotes the spherical surface of the sphere with center and radius . denotes the surface element of the sphere.
With the help of this formula you can immediately see that the Huygens principle applies in the 3D case. If the initial data or on a cuboid are disturbed, then this disturbance does not affect the solution for the points x 0 ∈ Q for large ones . You just have to choose the size that the spherical surface completely surrounds the square and therefore no longer have the disturbed data Q is integrated. Obviously must
be valid.
See also
Web links
- Huygens' Principle . MathPages (discussion and background of the principle from the point of view of modern physics, English).
- Reflection and refraction of light waves (explained by the Huygens principle) . (Animation)
Individual evidence
- ^ F. Graham Smith, Terry A. King, Dan Wilkins: Optics and Photonics: An Introduction . John Wiley & Sons, June 5, 2007, ISBN 978-0-470-01783-8 , pp. 240f. (Accessed September 8, 2013).
- ↑ Christiaan Huygens: Traité de la lumière . chez Pierre vander Aa, 1690 ( limited preview in Google Book Search - completed 1678).
- ^ Eugene Hecht: Optics . 2nd Edition. Addison-Wesley, 1987, pp. 392 ff .











![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![x_ {0} \ in [a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)













![R = [a, b] \ times [c, d]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3493a3bdcd7bd76960bb3d7b766bd6c6b1c4b3ee)







![Q = [a, b] \ times [c, d] \ times [e, f]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6160d6127da0655daf7d3dcc5f6e5c83a5dc9a0e)

