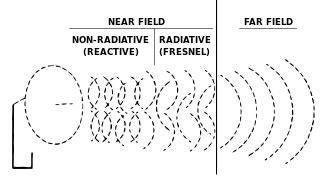
Near field and far field (antennas)

The terms near-field and far-field describe in antenna technology different spatial regions surrounded that radiating antenna systems. Based on the antenna system, the spatial areas are usually divided into three areas:

Near field, also known as reactive near field , is the area in the immediate vicinity of the antenna
This is followed by the transition field , also known as the Fresnel region or the radiating near field
The far field , also known as the Fraunhofer region, is the largest area in which the electromagnetic wave propagates as a plane wave in space, independently of the antenna.

The boundaries between the individual regions are dependent on the wavelength λ, have a flowing course and are not uniformly defined in the literature within the boundaries. For example, the transition field is also assigned directly to the near field and the transition areas are differentiated depending on the antenna size. The properties of the wave are described in the near field with the distance r from polynomials r ^{−n of} high order n . In the far field, at a large distance from the antenna, the description is reduced, since the first order ( n = 1, 1 / r dependence) dominates all other terms.

Definitions

Spatial areas around an antenna

Long antennas

With long antennas, these are antennas whose active elements have dimensions , the far field begins at a distance from the antenna ${\ displaystyle L> \ lambda}$ ${\ displaystyle r}$

{\ displaystyle r _ {\ text {fk}} = {\ frac {2 \ cdot L ^ {2}} {\ lambda}}.}

This distance is also known as the Fraunhofer distance, named after Joseph von Fraunhofer . The reactive near field is defined for long antennas according to

{\ displaystyle r _ {\ text {nb}} = 0 {,} 62 \ cdot {\ sqrt {\ frac {L ^ {3}} {\ lambda}}}.}

Long antennas are, for example, parabolic antennas . For example, with a parabolic mirror with an aperture diameter of 2 m and a frequency of 6 GHz, the far field begins at a distance of approx. 160 m from the parabolic antenna.

Short antennas

For short antennas, these are antennas whose dimensions active elements have, at a distance the far-field begins after ${\ displaystyle L <\ lambda}$ ${\ displaystyle r}$

{\ displaystyle r _ {\ text {fw}} \ gg {\ frac {\ lambda} {2 \ pi}}}

, d. H. ,

{\ displaystyle r _ {\ text {fw}} \ geq 2 \ lambda}

below that is the near field.

A short antenna is, for example, a dipole antenna . In the case of a λ / 2 dipole at a frequency of 6 GHz, according to the last definition, the far field begins at a distance of approx. 10 cm from the dipole.

Legal reference

In the case of definitions with a legal reference, as in the case of the Federal Network Agency with reference to the operation of radio systems , the reactive near field goes up to regardless of the antenna dimension

{\ displaystyle r _ {\ text {n}} = {\ frac {\ lambda} {2 \ pi}},}

then the radiating near field up to a distance of

{\ displaystyle r _ {\ text {f}} = 4 \ lambda,}

above that lies the far field.

With a λ / 2 dipole, again at a frequency of 6 GHz, according to this definition, the far field begins at a distance of approx. 20 cm from the dipole.

properties

Near field

Magnitude of the field wave resistance in the near and far field for an electric and magnetic dipole

The reactive near field in the immediate vicinity of the antenna is characterized by the fact that there is no radiation. Reactive power oscillates between the antenna and the environment in the near field , which has a direct effect on the antenna. By means of resonance circuits that are adjusted to the frequency, real power can be withdrawn from the antenna in the near field; this fact is exploited , among other things, with the dipmeter or electrical goods security labels based on the resonance principle. Electrically conductive materials in the near field influence the field strength curve and the antenna characteristics; this is used, among other things, with parasitic elements .

The relationships of the field strength in the near field depend on whether the antennas are primarily electrical or primarily magnetic:

An electric dipole as an antenna generates a high electric field strength in the near field , which, to a good approximation, decreases to the power of three with distance. The weaker magnetic field strength in the near field decreases quadratically with distance.

A magnetic dipole as an antenna generates a high magnetic field strength in the near field, which, to a good approximation, decreases to the power of three with distance. The weaker electric field strength decreases with the square of the distance.

These differences are expressed in a field wave resistance which, as shown in the diagram opposite, changes in the near field as a function of the distance from the antenna. Electric antennas with a dominant electric field have a field wave resistance that decreases in amount as a function of distance, while magnetic antennas have a low field wave resistance, the amount of which increases with distance.

The field wave resistance directly at the antenna is important for the reflection-free and adapted coupling of the antenna to the feed line and is ensured by adapting elements, with a distinction being made between the current and voltage supply.

With increasing distance from the antenna the field wave resistance levels off to the constant value of the field wave resistance of the empty space of approx. 377 Ω.

Transition field

Illustration of the ray paths

The transition field plays a role especially with long antennas. This can be viewed as an arrangement of smaller antennas that transmit out of phase with each other. When looking within the Fresnel region, the electric and magnetic field strengths decrease by approximately 1 / r and are in phase. For the irradiance at a specific location, the vectorial and in-phase sum of the individual rays ( Poynting vector ) must be calculated from all partial antennas . The irradiance adds up at some points and tends to zero at other points, but only one of the two field components of the rays is canceled.

Far field

In the far field, also named as the Fraunhofer region after Joseph von Fraunhofer , the magnetic field component and the electric field component are linked with each other in phase and via the field wave resistance of the empty space Z ₀ with approx. 377 Ω. For example, conclusions can be drawn about the magnetic field from the measured electric field in the far field and vice versa; this is not possible in the near field.

The two field components are oriented perpendicular to the direction of propagation. The resulting flat wave front is called the electromagnetic field and both field strengths decrease in strength with distance r by a factor of 1 / r .

In contrast to the Fresnel region, the in-phase sum of the individual rays is sufficient for observations in the far field. This greatly simplifies the calculation.

Qualitative comparison

The following table shows the qualitative differences between near and far field:

	Near field	Far field
Bearer of strength	"Virtual photon"	photon
energy	Stores energy. Can transmit energy via inductive or capacitive coupling	Energy spreads in space via a radiation field.
Duration	Disappears when source is turned off	Irrespective of the source, the radiation field spreads until it is absorbed
interaction	The measurement or withdrawal of power causes changes in power in the source in the form of voltage or current changes	The measurement absorbs part of the radiation field without affecting the source.
Field shape	Determined by the source and its geometry	Spherical waves that take on a more planar shape towards infinite distance.
Wave impedance	Depends on the source and medium	Depends only on the medium. In empty space 120 Ω π ≈ 377 Ω
guide	Energy can be specifically transported via electrical lines	Energy can be specifically transported in the form of waveguides

Example SAR antenna

Antennas with synthetic apertures are used in the exploration of the earth's surface by radar satellites . Their virtual aperture length is in the range of several hundred meters. This is necessary to achieve a good angular resolution. In an example with an aperture length of 200 m and a wavelength of 3 cm, the boundary between the near and far field is at r _far ≈ 2 · L ² / λ, in this case around 2600 km.

Most radar satellites orbit the earth in an orbit at an altitude of about 800 km, i.e. within the near field of the synthetic aperture. This results in complex correction calculations for the stored pulse periods of the individual source locations, which (because they are distance-dependent) have to be carried out individually for each point on the earth's surface. This correction is carried out via a phase correction of the echo signals from the radar. After this correction, the displayed image becomes significantly sharper, which leads to the term “focused SAR”.

literature

Jürgen Detlefsen, Uwe Siart: Basics of high frequency technology . 2nd Edition. Oldenbourg Verlag, Munich / Vienna 2006, ISBN 3-486-57866-9 .
Curt Rint : Handbook for Radio Frequency and Electrical Technicians . 13th edition. tape 2 . Hüthig and Pflaum Verlag, Heidelberg 1981, ISBN 3-7785-0699-4 .

Individual evidence

^ John D. Kraus: Antennas . 3. Edition. Mcgraw-Hill Higher Education, 2001, ISBN 0-07-123201-X .
↑ Constantine A. Balanis: Antenna Theory: Analysis and Design . 3. Edition. John Wiley & Sons, 2005, ISBN 0-471-66782-X .
^ Harold A. Wheeler: The Radian Sphere Around a Small Antenna . tape 47 . Proceedings of the IRE, Institute of Radio Engineers , August 1959, pp. 1325-1331 .
^ Term near field, glossary. Federal Network Agency, accessed on January 16, 2015 .
^ Term far field, glossary. Federal Network Agency, accessed on January 16, 2015 .
↑ BSI TR-03209-1 - Electromagnetic shielding of buildings - Theoretical principles. Federal Office for Information Security, 2008, accessed on February 7, 2018 .
^ Ron Schmitt: Electromagnetics Explained. A Handbook for Wireless / RF, EMC and High-speed Electronics . Newnes, 2002, ISBN 978-0-7506-7403-4 .

[kraus1-1] John D. Kraus: Antennas . 3. Edition. Mcgraw-Hill Higher Education, 2001, ISBN 0-07-123201-X .

[bala1-2] Constantine A. Balanis: Antenna Theory: Analysis and Design . 3. Edition. John Wiley & Sons, 2005, ISBN 0-471-66782-X .

[whel1-3] Harold A. Wheeler: The Radian Sphere Around a Small Antenna . tape 47 . Proceedings of the IRE, Institute of Radio Engineers , August 1959, pp. 1325-1331 .

[bnetza1-4] Term near field, glossary. Federal Network Agency, accessed on January 16, 2015 .

[bnetza2-5] Term far field, glossary. Federal Network Agency, accessed on January 16, 2015 .

[bsi1-6] BSI TR-03209-1 - Electromagnetic shielding of buildings - Theoretical principles. Federal Office for Information Security, 2008, accessed on February 7, 2018 .

[7] Ron Schmitt: Electromagnetics Explained. A Handbook for Wireless / RF, EMC and High-speed Electronics . Newnes, 2002, ISBN 978-0-7506-7403-4 .