Sinc function

The cardinal sinus , also si function , cardinal sinus or split function, is an analytical function . The name Cardinal Sine goes back to Philip M. Woodward from 1953. The nomenclature is not standardized in the literature, especially in the English-language literature, the designation is used for both the standardized and the non-standardized variant. In the German-language literature, a distinction is made between the two definitions and the non-standardized version as: ${\displaystyle \operatorname {sinc} }$

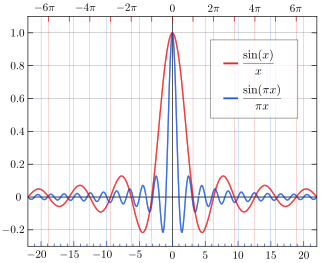
si ( x ): Non-normalized cardinal sinus

sinc ( x ) = si (π x ): normalized cardinal sinus

${\displaystyle \operatorname {si} (x)={\frac {\sin(x)}{x}}}$

Are defined. In information theory and digital signal processing , the application areas of the function, however, the standardized form with the designation is mostly used : ${\displaystyle \operatorname {sinc} }$ ${\displaystyle \operatorname {sinc} }$

${\displaystyle \operatorname {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}}$

The name for the non-standardized cardinal sine , which is common in German-speaking countries , should not be confused with the integral sine , the antiderivative of the -function. ${\displaystyle \operatorname {si} }$ ${\displaystyle \operatorname {Si} }$ ${\displaystyle \operatorname {si} }$

properties

General

At the liftable singularity at , the functions are continued continuously by the limit value or , which results from de l'Hospital's rule ; sometimes the definition equation is also written with case distinction. ${\displaystyle x=0}$ ${\displaystyle \operatorname {si} (0)=1}$ ${\displaystyle \operatorname {sinc} (0)=1}$

Software packages like Matlab mostly use the standardized function, which can also be expressed as a product or with the help of the gamma function as: ${\displaystyle \operatorname {sinc} }$ ${\displaystyle \Gamma (\cdot )}$

${\displaystyle {\frac {\sin(\pi x)}{\pi x}}=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{n^{2}}}\right)={\frac {1}{\Gamma (1+x)\Gamma (1-x)}}}$

The Taylor series of the -function can be derived directly from the -function: ${\displaystyle \operatorname {si} }$ ${\displaystyle \sin }$

${\displaystyle {\frac {\sin(x)}{x}}=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n+1)!}}=1-{\frac {x^{2}}{6}}+{\frac {x^{4}}{120}}\mp \cdots }$

The spherical Bessel function of the first kind is identical to the function: ${\displaystyle j_{0}}$ ${\displaystyle \operatorname {si} }$

${\displaystyle j_{0}(x)={\frac {\sin(x)}{x}}}$

zeropoint

${\displaystyle \operatorname {si} (x)={\frac {\sin(x)}{x}}=0}$ applies to ${\displaystyle \ x\in \{n\pi \ \mid \ n\in \mathbb {Z} \setminus \{0\}\}}$

${\displaystyle \operatorname {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}=0}$ applies to ${\displaystyle \ x\in \mathbb {Z} \setminus \{0\}}$

Maxima and minima

The extremes of si ( x ) coincide with their points of intersection (small, white points) with the cosine .

si ( x ) = sin ( x ) /  x

cos ( x )

The extremes of with a positive coordinate are a good approximation ${\displaystyle \operatorname {si} }$ ${\displaystyle x}$ ${\displaystyle x_{n},n\geq 1}$

${\displaystyle x_{n}\approx (n+{\tfrac {1}{2}})\pi -{\frac {1}{(n+{\frac {1}{2}})\pi }}}$

where a minimum is assumed for odd and a maximum for even . For the first extreme with a positive coordinate - the minimum at - the absolute error of the approximate value is already significantly smaller than 1/100. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle x_{1}\approx 4{,}49}$

In addition to these extremes and the absolute maximum at 0, the curve also has extremes due to its symmetry to the -axis . ${\displaystyle y}$ ${\displaystyle -x_{n}}$

Maxima and minima of si ( x ) = sin ( x ) / x

Maxima	Minima
0
	≈ 4.4934095 ≈ 1½π - 0.219284
≈ 7.7252518 ≈ 2½π - 0.12873
	≈ 10.904122 ≈ 3½π - 0.091452
≈ 14.066194 ≈ 4½π - 0.070973
	≈ 17.220755 ≈ 5½π - 0.057989
≈ 20.371303 ≈ 6½π - 0.049049
	≈ 23.519452 ≈ 7½π - 0.042493
≈ 26.666054 ≈ 8½π - 0.042998
	≈ 29.811599 ≈ 9½π - 0.033531
≈ 32.956389 ≈ 10½π - 0.030334
	≈ 36.100622 ≈ 11½π - 0.0276935
≈ 39.244432 ≈ 12½π - 0.025476
	⋯
⋯
	≈ (2n − ½) π - ((2n − ½) π) −1
≈ (2n + ½) π - ((2n + ½) π) −1

Fourier transform of the rectangular function

The sinc function is the Fourier transform of the rectangular function

${\displaystyle \operatorname {rect} \left({\frac {t}{\tau }}\right)=\chi _{[-\tau /2,\tau /2]}(t):={\begin{cases}1&|t|\leq \tau /2\\0&{\text{sonst}}\end{cases}}}$

because it applies

${\displaystyle {\mathcal {F}}(\chi _{[-\tau /2,\tau /2]})(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\tau /2}^{\tau /2}e^{-\mathrm {i} \omega t}\,\mathrm {d} t={\frac {1}{\sqrt {2\pi }}}\,\tau \,\operatorname {si} \left({\frac {\omega \tau }{2}}\right)}$  .

From the properties of the Fourier transformation it follows that the sinc function is analytical and therefore continuously differentiable as often as desired. From the Plancherel identity of the Fourier transform it follows that it is orthogonal to shifts of itself by integer multiples of , it is true ${\displaystyle \pi }$

${\displaystyle \langle \operatorname {si} (x-k\pi ),\,\operatorname {si} (x-l\pi )\rangle ={\frac {\pi }{2}}\int _{-1}^{1}e^{-\mathrm {i} (l-k)\pi t}\,\mathrm {d} t=\pi \operatorname {si} ((l-k)\pi )=\pi \delta _{l,k}}$  ,

where the Kronecker delta denotes. ${\displaystyle \delta _{l,k}}$

With a suitable normalization, these shifts in the sinc function thus form an orthonormal system in the function space  . The projection onto the subspace spanned by the results as ${\displaystyle L^{2}(\mathbb {R} )}$ ${\displaystyle \operatorname {sinc} (x-k\pi )}$

${\displaystyle P(f)(x)={\frac {1}{\pi }}\sum _{k=-\infty }^{\infty }\langle f(t),\,\operatorname {si} (t-k\pi )\rangle \;\operatorname {si} (x-k\pi )}$  .

Because of the interpolation property  , that is ${\displaystyle P(f)(n\pi )={\frac {1}{\pi }}\langle f(t),\,\operatorname {si} (t-n\pi )\rangle \;}$

${\displaystyle P(f)(x)=\sum _{k=-\infty }^{\infty }P(f)(k\pi )\;\operatorname {si} (x-k\pi )}$  .

Functions from this subspace are therefore uniquely determined by their values ​​at the points . ${\displaystyle \{k\pi :k\in \mathbb {Z} \}}$

The rectangular function as a Fourier transform of the function has bounded carriers and is therefore band-constrained together with the linear combinations of its displacements. Conversely, any band-restricted combination can be represented as such a linear combination and is therefore clearly determined by the function values ​​at the support points mentioned. That is the statement of the WCS sampling theorem . ${\displaystyle \operatorname {sinc} }$

Derivatives

The -th derivative of ${\displaystyle n}$

${\displaystyle \operatorname {si} (x)={\frac {\sin(x)}{x}}}$

can be determined analytically for everyone to: ${\displaystyle x\neq 0}$

${\displaystyle {\frac {\mathrm {d} ^{n}\operatorname {si} (x)}{\mathrm {d} \,x^{n}}}=\sum _{m=0}^{n}{\frac {n!}{m!}}(-1)^{n-m}{\frac {\mathrm {d} ^{m}\,\sin \,x}{\mathrm {d} \,x^{m}}}{\frac {1}{x^{n-m+1}}}={\frac {1}{x}}\left({\frac {\mathrm {d} ^{n}\,\sin \,x}{\mathrm {d} \,x^{n}}}-n{\frac {\mathrm {d} ^{n-1}\operatorname {si} (x)}{\mathrm {d} \,x^{n-1}}}\right)}$

The first two derivatives formed from this are:

${\displaystyle {\frac {\mathrm {d} \,\operatorname {si} (x)}{\mathrm {d} \,x}}={\frac {\cos \,x}{x}}-{\frac {\sin \,x}{x^{2}}}}$

${\displaystyle {\frac {\mathrm {d} ^{2}\,\operatorname {si} (x)}{\mathrm {d} \,x^{2}}}=-{\frac {\sin \,x}{x}}-{\frac {2\,\cos \,x}{x^{2}}}+{\frac {2\,\sin \,x}{x^{3}}}}$

surface

→ Main article : integral sine

The total area under the integral is

${\displaystyle \int _{-\infty }^{\infty }\operatorname {si} (x)\ dx=\pi }$

and accordingly

${\displaystyle \int _{-\infty }^{\infty }\operatorname {sinc} (x)\ dx=1}$.

Relationship to delta distribution

With the normalized sinc function, the delta distribution can be defined by the weak limit value:

${\displaystyle \lim _{a\to 0}{\frac {\sin \left({\frac {\pi x}{a}}\right)}{\pi x}}=\lim _{a\to 0}{\frac {1}{a}}\operatorname {sinc} \left({\frac {x}{a}}\right)=\delta (x).}$

The threshold that occurs is not an ordinary threshold because the left side of the equation does not converge. The limit value defines a distribution more precisely

${\displaystyle \lim _{a\to 0}\int _{-\infty }^{\infty }{\frac {1}{a}}\operatorname {sinc} \left({\frac {x}{a}}\right)\varphi (x)\,dx=\varphi (0)}$

for every Schwartz function . In the above equation, the number of oscillations per unit length of the sinc function goes towards infinity, but the function nevertheless oscillates for each in the interval . ${\displaystyle a\rightarrow 0}$ ${\displaystyle a}$ ${\displaystyle \pm {\frac {1}{\pi x}}}$

This definition shows that one should not think of the delta distribution as of an ordinary function that only takes on an arbitrarily large value. The Gibbs phenomenon shows a similar problem . ${\displaystyle x=0}$

application

Signal processing

The function is particularly important in digital signal processing . It occurs in the so-called sampling series (or cardinal series, ET Whittaker 1915), with the help of which a continuous band-limited signal is reconstructed from its sampled values or any sequence of interpolation points is continued to form a continuous signal: ${\displaystyle \operatorname {sinc} }$ ${\displaystyle x}$ ${\displaystyle x(k\Delta t)}$

${\displaystyle x(t)=\sum _{k=-\infty }^{\infty }{x(k\Delta t)\cdot \operatorname {sinc} \left({\frac {1}{\Delta t}}(t-k\Delta t)\right)}}$

This is the interpolation formula of the lowest fluctuation, i.e. This means that the frequency spectrum is limited and has the lowest possible highest (circular) frequency or frequency . If the requirement of band restriction is no longer given for the signal , i.e. if the output signal has components of higher frequencies, the sequence of these samples is too coarse-meshed, the high-frequency components are converted into additional low-frequency components, i.e. H. it occurs aliasing (mismatch of frequency components) on. ${\displaystyle {\tfrac {\pi }{\Delta t}}}$ ${\displaystyle {\tfrac {1}{2\Delta t}}}$ ${\displaystyle x}$

Diffraction at the slit

When waves are diffracted at a slit, the amplitudes form a diffraction pattern that can be explained by the Fourier transformation of a rectangular opening function. This is why the cardinal sine is also known as the split function . The brightness distribution perceived by the eye when light is diffracted is, however, the square of the wave amplitude; it therefore follows the squared function . ${\displaystyle \operatorname {sinc} ^{2}}$

Prime number distribution and nuclear physics

In physics, the function term describes the pair correlation distribution of the energies of the eigenstates of heavy atomic nuclei. In mathematics, he describes the pair correlation of the zeros of the Riemann zeta function associated with the distribution of prime numbers . The commonality lies in the two underlying theories of random matrices , which the physicist Freeman Dyson first pointed out in 1972 in an interview with the mathematician Hugh Montgomery . ${\displaystyle \textstyle \left({\tfrac {\sin(\pi x)}{\pi x}}\right)^{2}}$

Demarcation

The tanc function is structurally very similar to the split function, but is not one of the cardinal functions.

Web links

Commons : Sinc function  - collection of pictures, videos and audio files

• Sinc function at Wolfram Research

Individual evidence

1. ^ Charles A. Poynton: Digital video and HDTV . Morgan Kaufmann Publishers, 2003, ISBN 1-55860-792-7 , p. 147.
2. ^ Phillip M. Woodward: Probability and information theory, with applications to radar . Pergamon Press, London 1953, ISBN 0-89006-103-3 , p. 29, OCLC 488749777 . .
3. ↑ Fernando Puente León, Uwe Kiencke, Holger Jäkel: Signals and Systems . 5th edition. Oldenbourg, Munich 2011, ISBN 978-3-486-59748-6 .