Rainbow
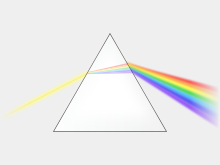
The rainbow is an atmospheric-optical phenomenon that is perceived as a circular arc-shaped colored band of light in a rain wall or cloud lit by the sun . Its radial gradient is the more or less whitened spectrum of sunlight. When entering and exiting, the sunlight is deflected by each almost spherical raindrop and broken down into light of several colors . In between it is reflected on the back of the drop . The light that leaves every drop is concentrated in colored layers that form thin cone coats stacked on top of one another . The observer has the rain cloud in front of him and the sun behind him. It receives light of a certain color from raindrops that are located on a narrow arc of a circle (a color strip of the rainbow) in the sky. The angle of observation is identical to the angle of the cone jacket in which this color is concentrated when it emerges from the raindrop.
In good light conditions in front of the rain wall, a secondary rainbow is visible above the strong main rainbow . This is weaker due to the double reflection of the light in the water droplets and has the opposite color sequence.
Character of sunlight and summary of rainbow formation (main rainbow)

middle stripe: rainbow section,
lower stripe: calculated rainbow colors
on the left in the middle and lower stripe: "surplus" rainbows
Sunlight is a small part of the spectrum of all electromagnetic waves . When the sun is high, all parts of the solar spectrum reach the surface of the earth and their mixture is perceived as whitish daylight . When the sun is low, the light color is redder, since the short-wave blue part of the solar spectrum is more strongly scattered in the atmosphere than the long-wave red, which for example leads to dawn .
The colors of the rainbow are created by the refraction of sunlight in the water droplets, whereby this is deflected to different degrees depending on the wavelength, like in a prism . In the rainbow, the colors are generally less pure and less clearly separated from one another than in the light spectrum generated, for example, with the aid of a prism spectroscope . The cause is the partial mixing of the colored lights separated when entering the water droplets due to their internal reflection at different points of the spherical droplet surface and their renewed deflection when exiting. Light rays of the same color from neighboring input rays can be combined, whereby they can be intensified or canceled out by interference .
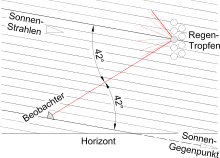
During or shortly after a rain event, the sunlight hitting the falling, closely spaced raindrops like a wall is reflected in a concentrated manner against the sun by each of them. Such a cone consists of cones with different cone angles that are inserted into each other for the different light colors. In the case of the main rainbow with a single internal reflection, the less deflected outer red light cone has an angle of about twice 42 °, the more strongly deflected inner blue an angle of about twice 40.2 °.
If the observer looks at the “rain wall”, he receives red light from drops, which, when viewed from him, are also located on a cone shell with an angle of about twice 42 °. The observer is at the top of this cone, the axis of which leads from the sun through the observer to the opposite point of the sun . The blue light on the inner edge of the rainbow comes from drops that are located on a cone shell with an angle of about twice 40.2 °. From each drop there is only one cone-shaped jet that reaches the observer. But because the number of raindrops is unimaginably large, a rainbow consisting of colored stripes is created with a striking brightness.
Ray path in the raindrop
The main rainbow is created by sunlight that penetrates a spherical drop of water, is reflected once inside and then exits the drop again.
If the entry angle is the angle to the vertical and the angle to the vertical in the water drop then applies according to the law of refraction
The refractive index of the water is dependent on the wavelength of the light .
The angle to the vertical at the entry inside the drop, the corresponding angle at the reflection and also at the exit from the drop appear in isosceles triangles with two side lengths equal to the radius of the drop. These angles are therefore all identical.
The total change in angle when passing through the drop is thus as
Maximum intensity occurs when the angle of the total deflection does not change with variation of the angle of incidence. This happens when the derivative according to the entry angle becomes zero, i.e.
This condition is met for the angle .
Multiple reflections
The secondary arc arises from two reflections within the drop. The change in angle can be calculated completely analogously for any number of reflections k = 1, 2, 3, ... :
Maximum intensity occurs at the entrance angle
where the derivative of the total deflection with respect to the angle of incidence is equal to zero.
Reflection, refraction and dispersion on a raindrop

A raindrop is transparent and, as it falls, is a small ball as a good approximation. The figure on the left shows the path of a sunbeam through a raindrop. When entering and exiting, the parts of the jet that are reflected at the edge of the droplet are not shown, and for the internal reflection, the exiting parts of the jet are not shown. These beam parts are not involved in the formation of the rainbow, they only reduce its intensity.
When entering, the different colored parts of the sunbeam are deflected to different degrees according to the color-dependent law of refraction , red the least, violet the strongest. Within the drop, the resulting color rays are reflected at not exactly the same points on the spherical rear wall. Nor does it emerge at a single, exactly the same point on the edge of the drop. The renewed deflection by refraction is also dependent on the color of each partial beam.
The figure on the right shows how all the light passing a drop is reflected back in a concentrated manner on the surface of a cone. To promote clarity, the process is shown for red light, that is, only for one of the colors contained in sunlight. The images for the other colors are slightly different. A typical difference is the angle of the bounding cone shell ( rainbow angle : 2 times 42 ° for red; 2 times 40.2 ° for blue). The illustration is a section through the center of the drop and sphere. There is rotational symmetry around the center axis drawn horizontally .
Colored lights from many raindrops are seen as rainbows
The figure on the right shows the angular relationships between observer, raindrop and sun. Since the sun ray entering the drop and the sun ray passing through the observer are parallel, a ray between the rainbow and the observer intersects both sun rays at the same alternating angles . In the picture, the observer sees a red beam emerging from a drop (alternating angle 42 °). Around the line between the observer and the sun's counterpoint, there is a rotational symmetry with respect to light consisting of additional raindrops. The rays of light reaching it from many drops are located on a cone envelope with the same opening angle as the opening angle of the cone-envelope spots of the raindrops.
In the figure on the left , two raindrops involved in the main rainbow are marked in the lower part (single internal reflection; the marked drops above concern the secondary rainbow, see following section). Small sections of the light from the blue cone-jacket spot (lower drop) and from the red cone-jacket spot (drop above) reach the observer. The drops of water are drawn exaggeratedly large. In reality every light color is seen from many small drops lying close together and behind one another and from an almost infinite number of drops lying on a circular band. The brightness is limited because, despite the concentration of light in the cone shells, only small sections of them can be seen.
The idea that blue should actually be the top color in the main arc as shown in the top left is wrong. Since blue emerges on a more pointed Kelmantel spot, the drops that provide the blue to an observer are closer to the center of the rainbow.

The fanning out of the main rainbow through dispersion is about 1.8 ° between red and blue. Because of the spatial extent of the sun of about 0.5 °, the width of each color is also about 0.5 °. This blurring is well below the fanning out, which is why the observer can still see a relatively pure red outer color. The other colors are less saturated or pure by mixing. Adding the finite extent of the sun and the fanning out results in the total width of the main rainbow of about 2.2 °. If the rain shower is 1 km away, raindrops are involved in the rainbow over a radial distance of about 35 m.

Seen from the earth's surface, the rainbow can only be a semicircle at its maximum ( apparent size of height 42 degrees, latitude 84 degrees). It occurs when the sun is on the horizon. The center of the semicircle is the opposite sun in the opposite horizon. When the sun is higher, the rainbow becomes smaller. Since its center is now below the horizon, the vertex becomes the orientation point. The rainbow is usually most pronounced in the vertex. If there are no raindrops at a certain point, the rainbow has a gap there.
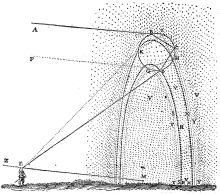
If the sun is higher than 42 °, the apex of the arc is also below the horizon and can therefore only be seen from an elevated point of observation, for example when looking from the top of a mountain or tower onto a lower rain wall (see picture left ).
In order to be able to see a main rainbow closed to form a circle, raindrops must be present in full radial extent around the opposite point of the sun and be illuminated by the sun. This option is generally only available from an airplane or a balloon (see picture on the right ).
Side rainbows and special forms
Side rainbow
So far, sun rays have been considered that are reflected once inside the raindrop. The secondary rainbow visible above the main arc arises from the smaller portion of the light, which only leaves the drops after two internal reflections. It is accordingly weaker than the main rainbow. A further weakening arises from the greater fanning out of the light beam into colored partial beams as a result of the flatter entry and exit at the drop edge. The secondary rainbow can therefore only be observed in favorable light conditions (see figure on the left ).
The light emerging after two internal reflections is concentrated in a cone envelope spot directed towards the opposite point of the sun. However, the double cone angle is greater than 180 ° - the surface of the cone resembles an umbrella turned inside out by the wind - so that spot light also falls backwards towards the observer (see figure below on the left ). The half cone angles are 129 ° (51 ° seen from the rear) for red light (see figure on the right ) and 126 ° (54 °) for blue light. Because the complementary angles of the cone envelope spot opening angle of 180 ° apply as alternating angles, the observer sees the reverse color sequence in the secondary rainbow compared to the main rainbow. The secondary rainbow is red on the inside and blue on the outside (see figure above right : upper rays).
Alexander's dark ribbon
In the picture on the right with a main and a secondary rainbow, it is noticeable that the sky inside the main arc appears significantly lighter than outside, and that the area between the main and secondary rainbow is significantly darker than its surroundings. This brightness contrast arises because the colors in the interior of the cone-jacket spots overlap and are finally reflected by the raindrops to the observer beyond the blue white light. Main and secondary rainbows are facing each other with their red side. The additional white light is missing here. The space between them is seen darker. This dark ribbon is called Alexander's dark ribbon in honor of its discoverer Alexander of Aphrodisias . In the case of the secondary rainbow, the cone jacket spots inside also contain less light (compare the illustration above on the right with the illustration above ), so that the brightening above it is less strong than below the main rainbow.
Tertiary and Quaternary rainbows
Secondary rainbows of a higher order, i.e. with more than two reflections within a raindrop, are no longer visible to the naked eye because of the attenuation described above; they were first described by Félix Billet (1808–1882), who also calculated the corresponding angular distances from the sun's counterpoint. However, after their existence was justified theoretically, it has also been proven by photographic means in recent years.
These are the tertiary rainbow at an angle of about 40 ° to the sun and the quaternary rainbow at about 45 °. These arcs are created by light that has been reflected three or four times within the raindrops.
Special forms
Lunar rainbow
Moon rainbow is the name of a rainbow at night that is based on moonlight . It is naturally much rarer than a rainbow and appears white to the observer because of its weakness of light. It can be seen because the human eye perceives differences in brightness much more sensitively than colors (see night vision ). When the air is clear and the moon is full, the rainbow colors can become visible. In addition, as a matter of principle, they can always be seen in color photographs if the process is light-sensitive enough that the lunar rainbow can be reproduced.
Fog bow
In drops with a diameter of less than 50 micrometers , the breakdown of sunlight into its colored components is too small. Fog contains correspondingly small water droplets, which is why this white rainbow is called a fog arc .

Dew arch
In the dew arch, light refraction takes place on dew drops, for example dew on a meadow or on cobwebs, rarely dew on small particles floating on a lake. The dew arch does not appear to the observer as a circle, but elliptical or hyperbolic, depending on the position of the sun and the inclination of the plane in which the dew drops are located. The effect results from the fact that the 42-degree cone of the reflected light intersects on the surface of the ground in a hyperbola or ellipse. The inclined conic section gives the idea that the light phenomenon extends in a horizontal plane, which is only apparently correct. In fact, in the observer's eye, the arc is always at a 42-degree angle from the sun's counterpoint.
Mirror arch
If the sunlight is reflected on a surface of water before it hits the raindrops, a second arch can be created, which meets the main arch on the horizon, but appears higher up like a second arch crossing the main arch. In addition, there have been observations of laterally offset, overlapping rainbows, the formation of which is still unclear.
Twin rainbow
The very rare split rainbows or twin rainbows differ from double rainbows made up of main and secondary rainbows in that they have a common origin, but then split (at least partially) into two rainbows, and the color sequence of the two arcs is not reversed. In contrast to the double rainbow, which is a coherent phenomenon that results from different refraction within the same amount of water droplets, a twin rainbow is actually two “independent” rainbows that arise at the same time from different amounts of water droplets. In particularly rare cases, each of the twin arcs can also show a secondary rainbow itself. Twin rainbows can arise when drops of water of different sizes fall from the sky at the same time, for example when two rain showers combine. The larger they are, the more the water droplets flatten out due to the air resistance and thus break the light in slightly different directions, which means that the rainbows that arise depending on the shape of the water droplets appear slightly deformed and can thus form a twin rainbow.
Interference, drop size and polarization
Interference arcs

When the light emerges from the drops, not only rays of different colors collapse, whereby the color purity of the rainbow is weakened by additive mixing. Rays of the same wavelength also coincide, which are mutually phase-shifted due to different lengths of travel in the drop . When they are superimposed, interference occurs, they cancel each other out or they reinforce each other. The patterns typical for interference phenomena accompany the main rainbow on its blue side as light and dark contrasting stripes, which are referred to as interference or redundant arcs .
The difference between the runways is a function of the drop size. Excess rainbows only appear with raindrops that are less than half a millimeter in diameter.
Influence of drop size and shape
The drop size and shape generally have an influence on the color of the rainbow.
The ends of the arc are often particularly bright. This effect is also caused by interference, which not only depends on the drop size but also on deviations from the spherical shape. In general, it can be said that large droplets with a diameter of several millimeters produce particularly bright rainbows with well-defined colors. If the size is less than 1.5 mm, the red color initially becomes weaker and weaker. Very small droplets, such as in clouds of fog , in which the diameter is often only about a hundredth of a millimeter, only produce washed-out colors.
polarization
The light reflected by a rainbow has a very high degree of polarization . With the help of a polarization filter, depending on the angle of rotation of the filter in front of the observer's eye or the camera, a rainbow can either be largely erased or its contrast increased.
Other celestial phenomena caused by dispersion
The optical effect of the dispersion of sunlight can also be observed in other optical phenomena than the rainbow. Above all, the halo phenomena are known .
- A 22 ° halo forms a circular wreath around the sun, but a rainbow usually only forms an arc with the sun at its back. Special halo phenomena are:
- Circumzenital arches only form very small sections from a concave arch, i.e. arched upwards.
- Circumhorizontal arcs occur when the sun is at an angle of at least 57.8 ° above the horizon and breaks into very high-floating hexagonal ice crystals.
- Side suns are another halo phenomenon, they stand next to the sun horizontally from the observer. They are small and do not have an arch shape.
Some phenomena are different from the rainbow caused by the diffraction of sunlight.
- Glories usually only appear when looking at a cloud from above . They are comparatively small and circular, by definition they are not rainbows, which in this case would be much larger and closed.
- Iridescent clouds sometimes have the color of a rainbow, but do not form an arc.
Occurrence
Natural rainbows usually arise when the sky clears up quickly after a rain shower and the low-lying sun illuminates the retreating area of precipitation . In temperate climates with a westerly preferred wind direction, such as in Central Europe , these conditions are often met in the late afternoon following a thermal thunderstorm . This mostly occurs with cold front elevators , with less rain falling on average in the morning than in the afternoon, which then also leads to a higher probability of encountering a rainbow.
In summer there is no rainbow to be seen around noon, as the sun is too high for this. In winter, however, it is also possible to see a flat rainbow at this time. Regardless, a rainbow can be seen in a spray quite often , especially around fountains , sprinklers, and waterfalls . Since such rainbows do not depend on a precipitation event, they are observed much easier and more frequently. With the appropriate position of the sun, rainbow fragments can also be observed in the spray of larger waves.
In weather without a cloudy sky with bright sunlight, the "rainbow" can be generated by yourself. Such an artificial rainbow is based on the same physical principles described. The only difference may be the size of the reflective surface. To find the apex of the rainbow, you have to direct your gaze towards your own shadow.
Distance and location of the rainbow
The rainbow is a multiple mirror image of the sun, created by a mirror consisting of a myriad of water droplets. However, this fact is not “as clear as day”, since the original sun is not depicted realistically as a small disc (viewing angle ≈ ½ ° for its diameter), but as a relatively large ring (main rainbow: viewing angle ≈ 42 ° for its diameter). We therefore ask ourselves at what distance the rainbow is in front of the landscape background, and we wonder why it “runs along” with us to the side and runs across the background. A simultaneous look into a common flat mirror (e.g. a wide window front) can explain the miracle: the rainbow is as far from us as the sun (it or the image of the sun in a flat mirror are superimposed on the background , because the drop mirror or the window pane are semi-permeable), and like the sun it can be seen at the moment in almost the same direction (no matter which place we take across the rainbow or the sun).
A ray of sunshine is not only reflected (on the back) by the water droplets, but also refracted. That is why we do not get rays of the sun from the virtual counterpoint of the sun, but from those drops that form the rainbow angle with it . So we don't see the sun as a small disc, but as a rather large but narrow ring. This is divided into even narrower, differently colored rings because the color components of the sunlight are refracted differently when entering and exiting the drops.
Chronology of the physical explanation
The rainbow not only inspires people's imagination, various attempts at explanation have also significantly advanced the cognitive process in physics and especially in optics .
The above-mentioned physical explanation of the rainbow is based in its fundamental ray-optical part on the work of René Descartes published in 1637 . They are described under the heading DE L'ARC-EN-CIEL in the appendix Les Météores of his philosophical work Discours de la méthode . He took up the idea developed by Dietrich von Freiberg in his work De iride et de radialibus impressionibus around 1300 , according to which a rainbow can be explained by the refraction and reflection of sun rays within individual droplets. His "mysterious" explanation of the colors of the rainbow was inaccurate. He applied the law of refraction , discovered shortly before by Willebrord Snell , without knowing the dispersion (the wavelength-dependent refraction of light).
A work by Edmond Halley on the rainbow dates from 1700 , and in 1704 Isaac Newton's theory of light brought dispersion into play and thus made the splendor of colors understandable.
While in Newton's time it was still the subject of controversial discussions as to whether light had a corpuscular or wave-like character, here too the rainbow was an important source of ideas. The riddle of the surplus arches prompted Thomas Young to carry out his famous double slit experiment in 1801 . With this he demonstrated the wave nature of light and was then able to solve the riddle by looking at interference phenomena (1804).
Young's theory was further refined in 1849 by George Biddell Airy . He explained the dependence of the exact color gradient on the droplet size. The specially developed mathematical processes still play an important role in modern quantum mechanics within the framework of the WKB approximation .
Modern physical descriptions of the rainbow and similar problems are essentially based on the theory developed by Gustav Mie in 1908 and named after him as Mie scattering .
Since the 1980s it has been possible to use a glass bead arc in school lessons to illustrate the rainbow and the effects of the observation position, in which glass bead abrasive applied to a black surface takes over the refraction of light.
Application in optical metrology
As described above, the rainbow angle in the case of spherical liquid droplets does not depend on the drop size, but only on the refractive index . This, in turn, is a temperature-dependent material constant of the drop-forming liquid at a certain wavelength . Therefore, by measuring the rainbow angle at which monochromatic laser radiation is reflected by a fog, the temperature distribution within the fog can be determined without contact if - as is usually the case in technical systems - it is known which liquid forms the fog.
Cultural meanings
As an unusual and impressive natural spectacle, rainbows have left their mark on the cultural history of mankind and are also a pictorial motif shown in countless works of art. Since the rainbow is known worldwide and has numerous positive attributes, it has repeatedly found its way into symbolism .
Religion and mythology
The rainbow has always been an important element of numerous mythologies and religions across all cultures and continents. The myths often assign him the role of a mediator or a bridge between gods and human beings. Mythologies without a rainbow are rare. The rainbow as a myth can also be found in the narratives of relatively isolated cultures; from this it can be concluded that this myth was independently conceived and handed down on earth in different places and at different times. If the rainbow myth can be found all over the world today, it is not solely due to traffic and exchanges among the great cultures of mankind.
The Australian natives , the Aborigines , revere a rainbow serpent in their creation story as the creator of the world and all living beings. The Greek mythology saw it as a link on which the goddess Iris travels between heaven and earth. According to Irish mythology , the leprechaun buried his pot of gold at the end of the rainbow. In Germanic mythology it was the bridge Bifröst , which connected Midgard , the world of men, and Asgard , the seat of the gods. During Ragnarök , the end of the world in Norse mythology, the rainbow is destroyed. Rainbow also appear in the creation story of the Diné . For the Inca , the rainbow represented the majesty of the sun.
- Babylonia
- In the Babylonian creation story Enuma Elisch ("As above ...", in the following Ee) it is told that the creator god Marduk made life on earth possible by killing the primordial flood, the goddess Tiamat. This fight was done with a bow (Ee IV, 35-40). In order to guarantee the permanent existence of creation, the highest god, the sky god Anu, took Marduk's bow and placed it in the sky as a "bow star". In the Babylonian myth the bow is deified: it is allowed to take a seat in the assembly of the gods and will be eternally successful (Ee VI, 87-94). In the ancient oriental world of ideas, the arch in the sky is a warlike symbol for the divine power to fight and conquer disturbances on earth and thus to secure life. Assyrian cylinder seal : A deity fights a demonic power with the bow star (1st millennium BC).
- Judaism and the Old Testament
 Joseph Anton Koch : Noah's offering of thanks (around 1803)
Joseph Anton Koch : Noah's offering of thanks (around 1803)
In the Tanach ( Gen 9 EU ) the rainbow is a sign of the covenant that God made with Noah and the people. According to the biblical story, God promised after the end of the flood : "From now on I will no longer curse the earth for the sake of people, because the poetry and striving of the human heart is evil from youth." ( Gen 8:21 EU ) The rainbow as The sign of peace between man and God thus takes up an ancient oriental tradition, according to which the phenomenon was interpreted as a lowered bow of God that was not ready to fire . Because of this location, the rainbow is an important religious symbol in Judaism to this day.
“And when it comes that I bring weather clouds over the earth, one should see my bow in the clouds. Then I want to remember my covenant between me and you and all living animals under all flesh, so that from now on there will be no more flood to destroy all flesh. "
- Christianity and New Testament
- Relief of Christ as judge of the world, sitting on a rainbow above the entrance portal of the Christ Church Flensburg - Mürwik by the sculptor Ursula Querner , from 1957
Another strand of tradition becomes important in Christianity. In Ezekiel 1 the prophet sees a huge throne chariot. On top of the throne there is a bright glow “like the sight of the arch that appears in the clouds on a rainy day. … This is what the glory of God looked like. ”( Eze 1.28 EU )
The rainbow appears only once in the Greek New Testament. In Revelation of John 10.1 EU an angel appears with a book from heaven, he is wrapped in a cloud and there is a rainbow over his head. This image is based on Ezekiel 1:28. The Greek word for this phenomenon is “iris”, and here it becomes clear that the ancient idea of the war bow has been forgotten. What is important about the appearance is the dazzling blaze of colors that connects heaven and earth. In addition to the rainbow, the Greek word also generally means a colored ring (or half-ring). In Rev 4,3 EU there is a rainbow in many German translations, but here it is expressly stated that it is a greenish shimmering wreath of light - a halo that shows God's presence. In the following Christian tradition, the symbol lives on icons and in medieval painting and sculpture. On altars and on Last Judgment depictions over the doorway of a church, Christ will sometimes be depicted as the judge seated on (or in) a rainbow - a free recording of the passages in Revelation mixed with Ezekiel. The rainbow here symbolizes the divinity of Christ. Since the 12th century, Mary has also been represented in a rainbow or sitting on a rainbow, thus expressing her holiness.
Visual arts


The rainbow is not only a motif in paintings by landscape painters , for example in the 19th century it was both more classical like Joseph Anton Koch and more romantic like Caspar David Friedrich . The natural phenomena associated with a rainbow, such as Alexander's dark band (see above), are also a popular motif in nature photography .
music
The rainbow is also often referred to in music. In 1939, in the pop song Over the Rainbow , Judy Garland sang about an area “somewhere above the rainbow” where “dreams come true”. This song by Harold Arlen and EY Harburg became a techno anthem as a cover version of Marusha in 1994 . Rainbow To The Stars by Dune also belongs to the same genre .
The French composer Olivier Messiaen , a synesthete , composed a movement in his "Quartet for the End of Time" ( Quatuor pour la fin du temps ) from 1944 with the title "Vortex of the rainbows for the angel who heralds the end of time" ( Fouillis d'arcs-en-ciel, pour l'Ange qui annonce la fin du temps ). In 1985 György Ligeti wrote one of his studies for piano Arc-en-ciel ("Rainbow").
The rock band The Rolling Stones described various drug experiences in their song She's A Rainbow in 1967 , using the blaze of colors of the rainbow as a metaphor for femininity.
The German hard rock band Scorpions called their second studio album from 1974 Fly to the Rainbow , which ends with the track of the same name.
Rainbow was a hard rock band formed in 1975 by guitarist Ritchie Blackmore . Rainbow's debut album includes the song Catch the Rainbow by Blackmore and singer of the band Ronnie James Dio .
With reference to the proverbial pot of gold at the end of the rainbow, the song All Of My Heart (1982) by the pop band ABC says: "No I won't be told there's a crock of gold at the end of the rainbow."
In the field of metal , the song At The End Of The Rainbow by the Swedish band Hammerfall should be mentioned, where you want to stand at the "end of the rainbow with gold in your hands" (on their 1998 studio album Legacy of Kings ). And the German band Axxis sings Touch the Rainbow (on their 1990 studio album Axxis II ).
reception
On February 7th, the first day of issue, Deutsche Post AG issued a postage stamp with a face value of 70 euro cents with the designation rainbow fragment in the series Heavenly Events . The design comes from Bettina Walter from Bonn.
Other symbolic uses
- In the New Age movement, the rainbow appeared as the logo for the first book series of the movement “New Age, Models for Tomorrow” and has since adorned numerous esoteric publications and products. Here, however, the rainbow has lost its symbolism and is only used to create positive feelings, harmony and wholeness.
- Parts of the Hamburg Green Alternatives List that left the party after the Bielefeld Federal Delegates' Conference of Bündnis 90 / Die Grünen at the beginning of 1999 were called Rainbow - For a New Left . Their representatives in the state parliament, the citizenry , were called the rainbow faction.
- The rainbow has rubbed off on language as well, as evidenced by terms such as rainbow press and rainbow trout . A private radio station in Baden-Württemberg is called Radio Regenbogen . The name of the aid organization AIDA eV is also composed of the respective first letters from the Portuguese Arco Iris do Amor (in German: Rainbow of Love ).
- Based on an Indian prophecy , according to which, after the devastation of the earth, warriors of the rainbow ("people of many colors, classes and beliefs") will populate the world, Greenpeace chose the rainbow as its symbol and baptized its flagship with the name Rainbow Warrior .
Rainbow flags
The rainbow flag is a symbol that has been used in history in many different ways :
- It was the flag of the ancient South American high culture of the Incas .
- During the Peasant Wars it symbolized the claim to a restoration of the covenant with God, in accordance with the Christian justification of its demands in the Twelve Articles as well as in Thomas Müntzer .

- Homosexuals of the late 20th and early 21st century see the rainbow flag with 6 colors as a symbol of tolerance and sexual freedom . More recently, particularly since the 2003 anti- Iraq war demonstrations , the Italian peace movement introduced a 7-color rainbow flag with the imprint Pace, Italian for peace . It now serves as a symbol for the international peace movement .
- The official flag of the Jewish Autonomous Region shows a seven-colored rainbow against a white background. The sequence of colors is reversed compared to the Italian peace flag.
literature
- Marcel G. Minnaert: Light and color in nature. Birkhäuser, Basel 1992, ISBN 3-7643-2496-1 .
- Herch Moysés Nussenzveig : The theory of the rainbow. In: Scientific American . Vol. 236, no. 4, April 1977, pp. 116-127.
- Kristian Schlegel: From the rainbow to the northern lights. Luminous phenomena in the atmosphere. Spektrum Akademischer Verlag, Heidelberg 2001, ISBN 3-8274-1174-2 .
- Michael Vollmer: Play of light in the air. Atmospheric optics for beginners. Spectrum Akademischer Verlag, Heidelberg 2005, ISBN 3-8274-1361-3 .
Web links
- Eugen Willerding: On the theory of the rainbow, glory and halos. (PDF; 2.7 MB).
- Dietrich Zawischa: About the rainbow. (PDF; 319 kB).
- Siegfried Wetzel: How is a rainbow created? The history of his declaration since Descartes.
- To interpret the inner rainbows. (PDF; 405 kB).
- Rainbows. Optics and explanatory pictures (English).
- What are “all the colors of the rainbow”? Excess rainbows, interference rainbows (English).
- The sign in the clouds. The colorful story of a colored symbol.
- Physically-Based Simulation of Rainbows. Simulations of rainbows depending on the shape and size of the water droplets.
Individual evidence
- ↑ Michael Vollmer: Light plays in the air. Atmospheric optics for beginners. Spektrum Akademischer Verlag, Heidelberg 2005, p. 116 f. and p. 124 ff.
- ^ Felix Billet: Mémoire sur les Dix-neuf premiers arcs-en-ciel de l'eau. In: Annales scientifiques de l'École Normale Supérieure. No. 1/5, 1868, pp. 67-109.
- ^ Triple Rainbows Exist, Photo Evidence Shows. At: ScienceDaily.com. October 5, 2011.
- ↑ Michael Theusner: photographic observation of a natural fourth-order rainbow . In: The Optical Society (Ed.): Applied Optics . 50, No. 28, October 1, 2011, ISSN 1559-128X , pp. F129-F133. bibcode : 2011ApOpt..50F.129T . doi : 10.1364 / AO.50.00F129 . PMID 22016236 . Retrieved October 6, 2011.
- ^ Michael Großmann, Schmidt, Elmar; Haußmann, Alexander: Photographic evidence for the third-order rainbow . In: The Optical Society (Ed.): Applied Optics . 50, No. 28, October 1, 2011, ISSN 1559-128X , pp. F134-F141. bibcode : 2011ApOpt..50F.134G . doi : 10.1364 / AO.50.00F134 . PMID 22016237 . Retrieved November 4, 2011.
- ↑ dew arch. At: meteoros.de.
- ↑ Marcel Minnaert: Light and color in nature. Birkhäuser Verlag, Basel / Boston / Berlin 1992, p. 257.
- ↑ Crossing rainbows. ( Memento of the original from November 7, 2008 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. Wilhelm Foerster Observatory Berlin, picture of the week, October 2000.
- ↑ The Rainbow of Reflected Sunlight. Section “Atmospheric Appearances” of the Vereinigung der Sternfreunde eV
- ↑ Unexplained rainbow phenomena. Section “Atmospheric Appearances” of the Vereinigung der Sternfreunde eV
- ↑ Atmospheric Optics: Twinned rainbows.
- ↑ Researchers unlock secret of the rare 'twinned rainbow'. At: ScienceDaily.com. August 6, 2012.
- ↑ Iman Sadeghi et al: Physically-based simulation of rainbows. ( Memento of the original from October 4, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (February 2012), ACM , Transactions on Graphics, 31 (1): 3.1-3.12.
- ↑ Beverly T. Lynds: About Rainbows.
- ↑ UQAC: René Descartes: Les Météores.
- ^ Claus Zittel (editor, translator and commentator): René Descartes - Les Météores / Die Meteore. Time leaps, volume 10, issue 1/2, Klostermann, Frankfurt 2006
- ↑ Edm. Halley: De Iride, Sive de Arcu Caelesti, Differtatio Geometrica, qua Methodo Directa Iridis Ntriusq; Diameter, Data Ratione Refractionis, Obtinetur: Cum Solutione Inversi Problematis, Sive Inventione Rationis Istius ex Data Arcus Diametro. Per Edm. Halley Reg. Soc. Soc. In: Philosophical Transactions of the Royal Society of London. 22, 1700, pp. 714-725, doi: 10.1098 / rstl.1700.0058 .
- ↑ a b J. B. Calvert: The Rainbow. ( Memento of the original from October 6, 2006 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Beverly T. Lynds: About Rainbows.
- ↑ Mikolaj Sawicki, Pawel Sawicki: Supernumerary Rainbows.
- ^ H. Moysés Nussenzveig: The theory of the rainbow. Scientific American, Vol. 236, No. 4, pp. 116-127 (April 1977).
- ^ Ritchie Blackmore's Rainbow. In: allmusic.com. Allmusic , accessed December 24, 2019.
- ^ Flag of the Jewish Autonomous Region in the flag dictionary.