crystal

A crystal is a solid whose building blocks - e.g. B. Atoms , ions or molecules - are regularly arranged in a crystal structure . Well-known crystalline materials are table salt , sugar , minerals and snow - but also metals . Due to the regular arrangement of the atoms or molecules, crystals do not have continuous, but discrete symmetries; one speaks of translation and long-range order .
The science of the properties and shapes of crystals is crystallography .
More precise definition, distinctions
A crystal is a homogeneous body because it is materially and physically uniform. But many physical properties are dependent on the spatial direction, i. H. a crystal is anisotropic .
Before 1992, crystals were defined by their periodicity : In this sense, a crystal is built up three-dimensionally and periodically from constant structural units. This structural unit is called a unit cell or unit cell .
According to the International Crystallographic Union IUCr , a crystal has been defined by its discrete diffraction orders (when illuminated with X-rays) since 1992 . So it has a long-range order , but is not necessarily periodic. This definition was enforced by the quasicrystals discovered in 1984 , which form a subgroup of the aperiodic crystals . Nevertheless, the periodic crystals form by far the largest subgroup of the crystals.
A distinction is made depending on the characteristics of the external shape
- unimpaired formed, so-called idiomorphic ( ancient Greek ἲδιος idios own and μορφἠ morph shape) crystals and
- xenomorphe (ancient Greek ξένος Xenos strange and μορφἠ morph shape) crystals whose outer shape by foreign interfaces is determined.
The outer shape of the idiomorphic crystal indicates the respective crystal structure. Therefore z. B. undisturbed grown sodium chloride crystals (table salt, mineral halite) cube-shaped. Even with idiomorphic crystals there is usually a certain distortion in nature, ie the edge lengths (but not the angles) can deviate significantly from the ideal shape (see law of constant angle ).
The external shape of a crystal is determined by the independent characteristics of crystal habit and crystal costume. The crystal faces as well as lattice planes are described by Miller indices .
Crystal types can also be differentiated by the type of bond between their building blocks (e.g. ionic crystal ).
Since the characteristic property of crystals is the regular arrangement in all three spatial directions , bodies are also conceivable whose building blocks are only repeated in one or two spatial directions. Then one can speak of one-dimensional and two-dimensional crystals. In nature, membrane proteins occur that are arranged as two-dimensional crystals in the biomembrane . One example is bacteriorhodopsin . In structural biology , 2D crystals are grown in order to determine the atomic positions of the crystallized macromolecules using electron cryomicroscopy .
Besides crystals there are also bodies that have no internal long-range order and are called amorphous . One example is glass (also known as lead crystal and other crystal glass ).
If a liquid is anisotropic and therefore exhibits some of the properties of a crystal, it is a liquid crystal .
Word origin
The term crystal comes from the Greek word κρύσταλλος krýstallos (to κρύος krýos “icy cold, frost, ice”). First of all, in Homer's work , it means “ ice ” - later everything similar to ice, light and transparent. Rock crystal in particular, but also colored gemstones and glass are so called (e.g. in Strabo and Claudius Aelianus ).
In the already ancient Greece powered mining probably were quartz crystals discovered. They were mistaken for ice that must have formed at such low temperatures that it could no longer melt. This view was widespread until the early Middle Ages. About the Latin Crystallus which has Old High German name crystallographic formed in the course of time to crystal has changed. In the 19th century, crystal was also used .
Structure and classification of periodic crystals

The direction and the length of the vectors , by which a crystal structure can be shifted so that the atomic positions are repeated, describe the axes of the crystal lattice (or crystal axes for short). Therefore, the structure of each type of crystal is represented with its own specific coordinate system , the axis system . In addition to the displacement, a crystal structure can also be mentally rotated around these axes until the rotated structure coincides with the original structure. Because the translational symmetry must be preserved, rotational symmetries can only occur that describe one, two, three, four or six repetitions in a complete rotation (360 °). We speak of 1-, 2-, 3-, 4- or 6-digit axes. There are crystals which, in addition to axes of rotation and translations, have other symmetry elements, namely mirror planes and inversion centers , as well as couplings between these symmetries to form rotational inversions , sliding reflections and screwing .
The symmetry properties are used for the classification of crystals. The number of conceivable combination and coupling possibilities of symmetry elements is limited (see also group theory ). There are 17 plane crystallographic groups in two-dimensional crystals and 230 crystallographic space groups in three-dimensional crystals , all of which are listed in the International Tables for Crystallography , Vol .
If a new crystal is examined, the space group is initially unknown. When describing the external shape of the crystal, it can only be assigned to one of 32 point groups (also called crystal classes). These point groups describe the macroscopic symmetry properties of the crystals and summarize those space groups which differ only in the translational symmetry. The translation does not play a role in the external observation of crystals. Because the angles between the crystal faces are the same for every type of crystal and are often compatible with a rotational symmetry (e.g. 90 ° for halite with fourfold rotational symmetry), seven crystal systems are used to describe the crystal morphology , in which the position and relative length of the Differentiate cell axes. A crystal is triclinic , monoclinic , orthorhombic , tetragonal , trigonal , hexagonal or cubic , depending on whether it belongs to the corresponding crystal system .
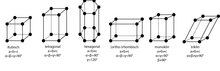
Auguste Bravais classified the various possible translation grids. These grids consist of the same parallelepipeds , the corners of which represent the grid points. In order to be able to describe the symmetry of certain lattices, he allowed not only primitive unit cells (with one lattice point per cell) but also larger unit cells that are face-centered or body-centered. An example of a face-centered unit cell is shown in Fig. 5. There are 14 Bravais grids in three-dimensional space .
In the crystal structure analysis , the scattering patterns of X-ray diffraction can be divided into eleven centrosymmetrical point groups, which are called Laue groups or Laue classes . Because even with non-centrosymmetrical crystal structures, centrosymmetrical diffraction patterns arise, since the reflections occur as Friedel pairs with normally the same intensity. The Lau groups can therefore be derived by adding a center of symmetry to the point group of the crystal.
The crystal structure is not substance-specific, i.e. a substance with a certain chemical composition can have different thermodynamically stable structures depending on external conditions (pressure, temperature). The different crystal structures of the same substance are called modifications ; the existence of various modifications is called polymorphism . The modifications represent different phases in terms of physical chemistry , the stability ranges of which can be represented in phase diagrams . In addition to any proper names, the individual modifications or phases of a substance are usually numbered consecutively with small Greek letters (for iron, for example, α- ( ferrite ), γ- ( austenite ), δ-, ε-iron; see iron Carbon diagram ).
Crystallization
A crystal is created when atoms or molecules form a regular structure with long-range order. In single-substance systems , crystallization takes place from another crystallized phase, from the steam or from the melt . In addition, crystals can form from multi-component systems, namely from a solution . To enable crystallization, the state of the atoms or molecules must not be in equilibrium. In the case of steam and solutions, one speaks of supersaturation , in the case of a melt, of undercooling .
Speed plays a role in the growth of the crystals. In the case of a melt, for example, the temperature must drop slowly enough below the melting point . Then the thermal movement of the individual atoms becomes so small that the mutual bonds can no longer be broken by vibrations - a uniform lattice is formed, which is characterized by long-range order. If, on the other hand, the temperature of the melt drops so quickly that the atoms cannot arrange themselves periodically, an amorphous material is created, a glass that only has a short-range order . The crystal lattice has a lower free enthalpy than glass .
The formation of a crystal is an exergonic process: Although the entropy in the system decreases (due to an increase in long-range order), at temperatures up to the melting point this is overcompensated by a decrease in enthalpy due to the attraction between the particles (= heat of crystallization).
The starting point for crystal formation is a crystal nucleus that grows as the temperature drops. If there are many such crystal nuclei or if crystallization starts in several places at the same time, a polycrystal is created . In many cases, two crystals of the same structure and composition but different orientation in space ( crystal twin ) grow together during crystallization .
Recrystallization is the change in a crystal structure due to changes in external factors such as pressure and temperature conditions. The crystalline solid changes its modification here .
The artificial production of crystals is known as crystal growing .
properties
Non-metallic inorganic crystals are harder , but also more brittle. As a rule, all metals solidify in crystalline form.
The behavior of light in crystals is described by the crystal optics . Important properties and phenomena associated with this are optical activity , polarization , birefringence and pleochroism . Periodic dielectric structures, so-called photonic crystals , show novel optical properties.
Some crystals, e.g. B. quartz crystals have piezoelectric properties. They build up an electrical voltage when they are deformed and deform when an electrical voltage is applied. This effect is in piezo lighters used to spark generate. In the electronics piezoelectric serve quartz oscillators as clock (eg. As in quartz watches ). Some, but not all, piezoelectric crystals convert a temperature difference into charge separation. This property is called pyroelectricity . Such crystals are used in motion detectors and temperature sensors. A special case of pyroelectricity is ferroelectricity : In ferroelectric crystals, the polarization of the electrical polarization can be reversed by applying a voltage.
Lattice failure
A real crystal contains lattice defects , which means that the three-dimensional periodic arrangement of the atoms is disturbed. There are point errors, line errors, area errors and volume errors. Point errors are the only lattice errors that also occur in thermodynamic equilibrium .
Forms and examples
Single crystal and poly crystal
As a rule, a crystalline solid is present as a polycrystal and not as a single crystal, i.e. it consists of many small crystals ( crystallites ) that are separated from one another by grain boundaries . For example, metal objects, wires, etc. are usually polycrystals. There is a body of different crystal types , the interfaces between them are called phase boundaries .
Minerals
Many minerals are able to develop a variety of crystal shapes and colors. The best- known examples are, on the one hand, quartz , whose forms cover the entire range from macrocrystalline-colorless ( rock crystal ) to microcrystalline-colored ( agate ) and, on the other hand, calcite with a similar wealth of varieties .
The world's largest crystals were discovered in the Naica mine . They consist of the gypsum type Marienglas , are up to 14 m long and weigh up to 50 tons.
The diamond , a crystalline form of carbon , is the hardest naturally occurring mineral. Also silicon crystallizes in the diamond type .
Technical applications
Silicon is currently the substance that is most frequently used in large quantities as a single crystal (monocrystal), namely in semiconductor technology . The gallium arsenide (GaAs) used there, however, has the so-called zinc blende structure. Nanotechnology deals, among other things, with nanocrystals .
Organic crystals
Organic substances, e.g. B. the proteins , form crystals - but only in exceptional cases. For example, catalase crystals are found in the peroxisomes of plants , which can be visualized using electron microscopy . The protein crystallography is concerned with the crystal growth of proteins for structural analysis .
Colloids
Colloids typically form paracrystals because not all building blocks are identical, the building blocks themselves are typically anisotropic, and because strong and weak bonds between atoms and groups of atoms coexist. Monodisperse hard-sphere suspensions, on the other hand, can form crystals because the building blocks are all identical and isotropic.
literature
- Walter Borchardt-Ott: Crystallography. Springer, Berlin 2002. ISBN 3-540-43964-1 .
- Dorothy G. Bell: Group Theory and Crystal Lattices. In: Review of Modern Physics. Volume 26, No. 3, 1954, p. 311.
- Charles Kittel : Introduction to Solid State Physics. Oldenbourg, Munich 2002. ISBN 3-486-27219-5 .
- Will Kleber , Hans-Joachim Bautsch , Joachim Bohm : Introduction to crystallography. Verlag Technik, Berlin 1998. ISBN 3-486-27319-1 .
- Werner Massa: Crystal structure determination. Teubner, Wiesbaden 2009. ISBN 978-3-8348-0649-9 .
- Ulrich Müller: Inorganic Structural Chemistry. Teubner, Wiesbaden 2004. ISBN 3-519-33512-3 .
- Lesley Smart, Elaine Moore: An Introduction to Solid State Chemistry. Vieweg, Wiesbaden 1997, ISBN 3-528-06773-X .
- Robert F. Symes and RR Harding: Gemstones & Crystals. Mysterious treasures of the earth; Appearance, development, processing , Gerstenberg Verlag, Hildesheim 1991, ISBN 3-8067-4560-9 .
Web links
- Mineral Atlas: Crystal (Wiki)
- The Giant Crystal Project - Documentation of the largest crystals in the world
- Information about the crystal system and crystal synthesis
- Alpine minerals - crystal
Remarks
- ↑ Rotational inversions consist of rotation and inversion; they are usually marked with etc.
- ↑ Glide reflections consist of translation and reflection; Symbol depending on the translation axis
- ↑ Screws consist of rotation and translation; z. B. is the symbol for rotation by 180 ° and translation by half a grid vector
Individual evidence
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 14.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 19.
- ^ "Online Dictionary" of the International Crystallographic Union (Eng.).
- ↑ Hayato Yamashita, Kislon Voitchovsky, Takayuki Uchihashi, Sonia Antoranz Contera, John F. Ryan and Toshio Ando (2009): Dynamics of bacteriorhodopsin 2D crystal observed by high-speed atomic force microscopy, Journal of Structural Biology, Volume 167, Issue 2, Pages 153-158, ISSN 1047-8477 , doi : 10.1016 / j.jsb.2009.04.011 .
- ↑ Michael G. Rossmann and Eddy Arnold, eds. (2001): International Tables for Crystallography Volume F: Crystallography of Biological Macromolecules. Kluwer Academic Publishers, Dordrecht u. a., pages 459f.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 199.
- ^ Wilhelm Pape : Concise dictionary of the Greek language. Concise Greek-German dictionary. 3rd edition, Braunschweig 1914.
- ↑ Wolfgang Pfeifer u. a .: Etymological dictionary of German. dtv, Munich 1995, ISBN 3-423-03358-4 , page 735.
- ↑ a b Helmut GF Winkler (1950): Hundert Jahre Bravais lattice. Die Naturwissenschaften, Volume 37, Number 17, pp. 385-390, doi : 10.1007 / BF00738360 .
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 17.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 23.
- ^ Siegfried Haussühl (1993): Kristallgeometrie. Weinheim Publishing House. ISBN 3-527-29018-4 , page 66.
- ↑ Werner Massa (1996): Crystal structure determination Teubner Verlag. ISBN 3-519-13527-2 , page 60ff.
- ^ Siegfried Haussühl (1993): Kristallgeometrie. Weinheim Publishing House. ISBN 3-527-29018-4 , page 57.
- ^ Theo Hahn, Ed. (2005): International Tables for Chrystallography, Volume A. Springer Verlag. ISBN 0-7923-6590-9 .
- ↑ Zbigniew Dauter and Mariusz Jaskolski (2010): How to read (and understand) Volume A of International Tables for Crystallography: an introduction for nonspecialists. J. Appl. Cryst. ( ISSN 0021-8898 ), 43, 1150–1171, doi : 10.1107 / S0021889810026956 , online (PDF; 3.3 MB) accessed on December 20, 2010.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 67.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 22.
- ^ Theo Hahn, Ed. (2005): International Tables for Chrystallography, Volume A. Springer Verlag. ISBN 0-7923-6590-9 , page 762.
- ↑ Will Kleber, Hans-Joachim Bautsch, Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 202
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , pp. 267-272.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 262.
- ↑ Will Kleber, Hans-Joachim Bautsch and Joachim Bohm (1990): Introduction to Crystallography. Publishing house technology. ISBN 3-341-00479-3 , page 264.
- ↑ GEO Magazine No. 05/08. Speleology: In the Chamber of Crystal Giants , p. 2 of 4 .
- ↑ Elmar Weiler and Lutz Nover (2008): General and molecular botany. Georg Thieme Verlag, Stuttgart and New York. ISBN 978-3-13-147661-6 , page 73, Fig. 2.21 and page 327, Fig. 10.8.