Bravais grid
The Bravais lattices are a classification of the possible lattice systems (translation groups) in crystallography :
with integers and linearly independent vectors (in the case of three dimensions) that span the grid ( primitive vectors ). Bravais grids are part of the classification of space groups (and the mathematical derivation of the classification of Bravais grids can be found in the related literature). The Bravais grids are thus a classification of the possible translation groups of regular point grids.
There are fourteen Bravais grids in three dimensions.
In the representation of the Bravais lattice, one traditionally starts from the point groups and their division into seven crystal systems (or 32 crystal classes, types of point groups). The Bravais lattices arise from the basic cell of the crystal system through translation and they are constructed by adding further lattice points to the basic cell. The basic cell is adapted to the symmetry group of the crystal system (compare the discussion under the unit cell and the illustration below). For the Bravais lattice, in general, additional lattice points have to be added (the base cell chosen as the starting point does not correspond to the primitive unit cell of the lattice). This can be done in six possible ways: face-centered - in opposite sides (A, B, C) or in each face (F) - body-centered (I) and primitive (P, i.e. no addition of additional grid points).
While the point group symmetries are visible in the outer crystal form and consist of the symmetry elements rotation, mirroring, inversion and rotation inversion , the translations in the Bravais lattices are added, which are of microscopic order of magnitude ( Ångström ) in the crystal lattice and not in the outer crystal form visible.
All grid points are considered to be equivalent. When describing the crystal structure , the mathematical lattice (defined by the possible translations) is generally supplemented by the description of the base , which can also consist of several atoms (crystal structure is the same as the lattice plus base).
Auguste Bravais classified the various possible translation grids around 1849 by placing the same parallelepiped cells next to one another in all directions. The corners of the cells then result in a three-dimensional point grid, which in the real crystal represents the focal points of the crystal building blocks (e.g. atoms or molecules).
In general, the generating parallelepiped is an oblique prism with all three side lengths and angles different from each other. In this case it is a triclinic crystal system. If the side lengths and / or angles meet further conditions, higher symmetries can result. The cubic crystal system, for example, requires right angles and cell edges of equal length. Bravais noticed that there are types of lattice that have a special feature: their symmetry is higher than would be easily recognizable from the smallest possible cell. With Halit it is possible to choose half the surface diagonal of a cube as a translation. The resulting lattice, however, has a rhombohedron with an angle of 70 ° 31 '44 "as the smallest parallelepiped. For reasons of symmetry, it is much more practical to take a cube from the lattice as a so-called unit cell . This cubic unit cell is larger than the rhombohedron and contains the In the middle of each surface another grid point, this grid is called face-centered cubic .
use
The actually purely mathematical term of the Bravais lattice is often used in the natural sciences, such as crystallography , mineralogy , materials science , solid-state chemistry or solid-state physics , as the arrangement of the atoms within a crystal can be systematically described in this way. However, not every lattice point is necessarily represented by an atom: The Bravais lattice only provides the mathematical framework that is filled in a crystal structure by atoms (the base). The crystal structure thus consists of the lattice and the base, which is repeated at every lattice point, and is understood as a fundamental principle in crystallography. So z. As the NaCl structure of a face-centered cubic lattice and a diatomic base of a respective Na - cation and Cl - anion .
It has a special meaning in the structure elucidation of crystals (especially X-ray crystallography ). The Bravais lattice of the crystal can be determined on the basis of the metric of the reflexes in the reciprocal space and their systematic integral cancellation .
classification
The Bravais lattices are assigned to the seven crystal systems based on their point group . If the basic cell of the Bravais lattice corresponds to a primitive unit cell of the crystal lattice - it then has the smallest possible volume (the cell contains one point) - one speaks of a primitive lattice.
The further differentiation of the seven crystal systems to the 14 Bravais lattices takes place through the arrangement of further lattice points, either in the center of the room (body- centered or body- centered ), on the centers of all boundary surfaces ( surface-centered ) or on the centers of the two base surfaces ( base- centered ) of the unit cell.
In the following the Bravais lattices are arranged according to the crystal systems with decreasing symmetry .
Right-angled (orthogonal) axis systems
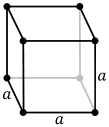
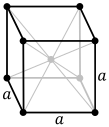
Cubic crystal system
- highest symmetry
- three axes of equal length at a 90 ° angle
cubic -primitive
-body-centered
-face-centered
(sc: simple cubic) (bcc: body centered cubic) (fcc: face centered cubic)
Tetragonal crystal system
- two axes of equal length, three 90 ° angles
tetragonal -primitive -body-centered
Orthorhombic crystal system
- also rhombic crystal system
- three 90 ° angles, no axes of equal length
orthorhombic -primitive -base-centered -body-centered -face-centered
Skew-angled axis systems
Hexagonal crystal system
- two axes of equal length in one plane at an angle of 120 °, the third axis perpendicular to it
hexagonal primitive
Trigonal crystal system
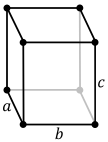
- Trigonal crystal structures can also be described in the hexagonal lattice:
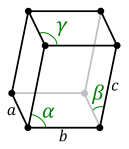
- hexagonal arrangement: a = b ≠ c, α = β = 90 °, γ = 120 ° (see figure above)
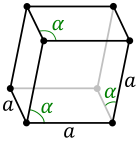
- A rhombohedral centering can occur as a special case:
- three axes of equal length, three equal angles not equal to 90 ° (see figure below)
- not to be confused with the orthorhombic crystal system
rhombohedral
Monoclinic crystal system
- two 90 ° angles, no axes of equal length
monoclinic -primitive -base-centered
Triclinic crystal system
- lowest symmetry of all grids
- no equal angles, no equal axes
triclinic
Hermann Mauguin symbolism
In the Hermann Mauguin symbolism (see also point position ):
- Triklin, P 1
- Monoclinic: primitive P 2 / m , base-face-centered C 2 / m
- Orthorhombic: primitive Pmmm , body centered Immm , base face centered Cmmm , face centered Fmmm
- Hexagonal: P 6 / mmm
- Rhombohedral: R 3 m
- Tetragonal: primitive P 4 / mmm , body centered I 4 / mmm
- Cubic: primitive Pm 3 m , body-centered Im 3 m , face-centered Fm 3 m
Bravais lattice in non-three-dimensional spaces
In two-dimensional there are five Bravais lattices, four of which are primitive: the oblique angled lattice and four special types: the square, the rectangular, the hexagonal and the centered rectangular lattice, which is the only one that is not primitive. The surface of all three-dimensional grid types consists of these two-dimensional grid types. They are therefore of great importance in surface physics and nanotechnology.
In the four-dimensional there are 64 Bravais lattices (10 of them break down into enantiomorphic pairs, if you do not count this, there are 54).
See also
Web links
Individual evidence
- ↑ z. B. Johann Jakob Burckhardt The movement groups of crystallography , 2nd edition, Birkhäuser, 1966.
- ↑ Okrusch, Matthes Mineralogie , Springer Verlag 2005, p. 9f.
- ^ Helmut GF Winkler (1950): Hundred years of Bravais lattice. In: Die Naturwissenschaften, Volume 37, Number 17, Pages 385-390 doi: 10.1007 / BF00738360 .
- ^ Sanat Chatterjee Crystallography and the World of Symmetry , Springer Verlag 2008, p. 28f (section Bravais grid).
- ^ Bravais: Treatise on the systems of points regularly distributed on a plane or in space , Leipzig 1897, French original J. Ecole Polytechnique, Volume 19, 1850, pp. 1–128.
- ↑ Martin Henzler, Wolfgang Göpel: Surface physics of the solid . Teubner, Stuttgart 1994, ISBN 3-519-13047-5 .
- ↑ Harold Brown, J. Neubüser, H. Wondratschek, R. Bülow, Hans Zassenhaus Crystallographic groups of four dimensional space , Wiley 1978.