Birefringence

ordinary and extraordinary rays are visible through red fluorescence in the crystal
The double refraction or birefringence is the ability of optically anisotropic media , a light beam into two mutually perpendicular polarized to separate sub-beams (ordinary and extraordinary ray). The cause of this effect lies in the different refractive index ( n o and n ao ) depending on the direction of propagation and the polarization of the light.
A prominent example of such a material is calcite (also called calcite or double spar), on which the birefringence was discovered by Erasmus Bartholin in 1669 .
Optically isotropic materials (e.g. in the cubic crystal system ) can also become birefringent due to external influences. Such influences are e.g. B.
- mechanical stress (deformation or stress birefringence, see stress optics )
- Textures and residual stresses in shaping
- electric fields (electric birefringence, electro-optical Kerr effect )
- magnetic fields (magnetic birefringence, Cotton-Mouton effect , generally see magneto-optics )
- internal friction and related textures in flows of highly viscous liquids.
Most liquid crystals are spontaneously birefringent.
Closely related or connected to birefringence is dichroism , in which colors are absorbed in a polarization-dependent manner.
Physical cause
Birefringence occurs in optically anisotropic crystals . These have a different index of refraction for different polarization and direction of the incident light.
The corresponding index ellipsoid can be:
- optically uniaxial or uniaxial , d. H. have an optical axis and two different major refractive axes or indices of refraction; this is the case in the whirling crystal systems ( trigonal , tetragonal and hexagonal )
- optically biaxial or biaxial , d. H. have two optical axes and three different main refractive axes or refractive indices. This is the case in the orthorhombic , monoclinic and triclinic crystal systems . In general, both refracted rays are extraordinary here ( electric field and electric flux density do not have the same direction, whereby the propagation vector is not - as is usual - perpendicular to , but to , see literature).
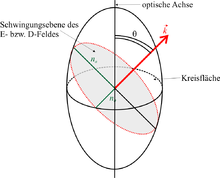
The optical axes of a birefringent crystal should not be confused with the optical axis of a system of lenses and mirrors.
Ordinary and extraordinary beam

The ordinary ray and the extraordinary ray are defined by the orientation of their electric field to the plane, which is spanned by the optical axis and the direction of propagation of the incident ray ( main section ):
- The ordinary ray is the portion of the incident ray whose electric field is perpendicular to the main section. For the ordinary ray in uniaxial crystals, Snellius' law of refraction applies to isotropic media, i.e. H. it is not refracted at normal incidence on the birefringent crystal . The elementary waves of the ordinary ray form spherical waves that satisfy Huygens' principle .
- The second, the extraordinary ray , on the other hand, is the part of the incident ray whose electric field oscillates in the main section of the crystal. The law of refraction does not apply to him , i.e. H. it will also be refracted at normal incidence on the birefringent crystal. The elementary waves of the extraordinary ray form ellipsoids of revolution .
The wave fronts for the ordinary and the extraordinary ray propagate at different speeds and , from this the associated refractive indices follow:
and
with the speed of light c in a vacuum .
The difference in the refractive indices ( ) is a measure of the birefringence. The sign is called the optical character or optical orientation . For calcite is . Calcite is therefore an optically negative uniaxial crystal, i. H. in it the extraordinary ray moves faster than the ordinary one:
In this context, one speaks of the fast and the slow axis . In an optically negative uniaxial crystal, the fast axis is parallel to the optical axis of the crystal and the slow axis is perpendicular to it.
Accordingly, in an optically positive uniaxial crystal, the extraordinary ray moves more slowly than the ordinary one:
Therefore, in an optically positive uniaxial crystal, the fast axis is perpendicular to the optical axis of the crystal, while the slow axis coincides with the optical axis.
Circular birefringence

The property of optically active substances to show a different refractive index for left and right circularly polarized light is called circular birefringence .
It was first described on quartz by Dominique François Jean Arago in 1811 . There the effect is about a factor of 100 less than the linear birefringence. Since the two effects are superimposed, the circular birefringence can only be observed when the linear birefringence does not occur. With quartz this is the case along the optical axis.
In order to calculate the rotation of a linearly polarized beam due to the circular birefringence in a material, it can be described as a coherent superposition of a left-hand and a right-hand component with the same intensity. The two parts move through the material at different phase velocities (the greater phase velocity corresponds to the smaller refractive index). After the material has passed through, the superposition of the two parts again results in a linearly polarized beam. The phase difference Δφ of the two components after the material has passed through is shown in a rotation of the polarization plane of vibration by the angle Δφ / 2 with respect to the vibration plane before the material has passed through. With quartz, this angle is ± 21.7 ° / mm of material thickness (±, since quartz occurs both clockwise and counter-clockwise).
- A right turn is described with a positive angle of rotation and occurs when the refractive index for the left rotating portion is greater than that for the right-handed fraction: .
- A left turn is described with a negative angle of rotation and occurs when the refractive index of the right rotating portion is larger than that for the left-handed percentage: .
The cause of the circular birefringence in quartz is its " helical " crystal structure. But not only crystalline materials with a "helical" structure show a rotation ability of the polarization plane, liquids also have this property, e.g. B. Turpentine . The reason for this also lies in their molecular structure, which is called chirality . Furthermore, a circular birefringence can be induced by a magnetic field, see Faraday effect , e.g. B. lead silicate glass.
There are also comparable effects for the absorption behavior of materials, see circular dichroism .
Birefringent materials
properties
The tables contain the refractive indices of common uniaxial or biaxial systems at the wavelength of orange-red light:
|
|
application
Birefringent materials are e.g. B. used in retardation plates and polarizers . The birefringent polarizers include the Nicol prism or the Glan-Thompson prism . They make it possible to generate linearly polarized light from unpolarized light.
In the case of optical images , birefringent materials can be used as an optical low-pass filter , for example to reduce the aliasing effect that occurs in connection with Bayer sensors .
Birefringence can also occur as a disturbing effect, e.g. B. in injection compression molding of compact discs . The birefringence is caused here by mechanical stresses within the polycarbonate layer, for example by thermal stress or shear stress on the material.
Various theories suggest that birefringence with sunstones was a historical tool for determining the position of the sun and navigating ships when the sky was overcast .
proof
When the sample is rotated between crossed polarization filters, the brightness or the color of the birefringent object changes, while optically isotropic materials show no changes in the image.
The detection of a birefringent substance can therefore, for. B. also take place in a polarizing microscope .
It is also possible to identify birefringent materials using the immersion method.
literature
- Werner Döring: Introduction to Theoretical Physics, Volume III (Optics). Göschen Collection, Berlin 1957.
- Niederig, Heinz., Eichler, Hans-Joachim., Bergmann, Ludwig., Schaefer, Clemens .: 9th edition De Gruyter, Berlin 1993, ISBN 3-11-012973-6 , p. 496 ff
Web links
Individual evidence
- ↑ Wolfgang Zinth, Ursula Zinth: Optics . Oldenbourg Wissenschaftsverlag, 2005, ISBN 978-3-486-27580-3 , p. 230 .
- ^ Hans-Joachim Bautsch , Will Kleber , Joachim Bohm : Introduction to crystallography . Oldenbourg Wissenschaftsverlag, 1998, ISBN 978-3-486-27319-9 , p. 273 .
- ↑ a b Wilhelm Raith, Clemens Schaefer: Electromagnetism . Walter de Gruyter, 1999, ISBN 978-3-11-016097-0 , p. 425-426 .
- ↑ a b Glenn Elert: Refraction . In: The Physics Hypertextbook . Archived from the original on September 17, 2009. Info: The archive link was automatically inserted and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. Retrieved December 21, 2010.
- ^ R. Wimberger-Friedl: Analysis of the birefringence distributions in compact discs of polycarbonate . In: Polymer Engineering & Science . tape 30 , no. 14 , 1990, pp. 813-820 , doi : 10.1002 / pen.760301403 .