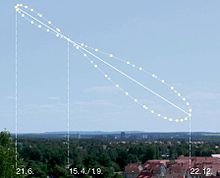
Position of the sun

Sun position diagram ( altitude above azimuth )
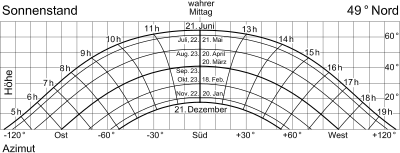
for all locations with φ = 49 ° North
parameterized with true local time on hour lines and annual data on declination lines.

The Sun is provided with the coordinates of the horizon height and direction ( azimuth specified) position of the sun in the sky via a observation . It changes over the day as a result of the earth's rotation and over the year as a result of the earth's orbit around the sun.

A sun position diagram is used for illustration . I. d. Usually the relationship between altitude and azimuth is shown in an axis diagram. With the help of two sets of parameters , the equatorial coordinates hour angle (time of day) and declination angle (date of year) are also displayed.

The daily change in the position of the sun (daily course of the sun) is characterized by 3 striking points, which are the following: sunrise (in Central Europe between northeast and southeast), midday high (in the south) and sunset (between northwest and southwest). In the morning or in the evening, the sun is low, and around noon (especially in the summer months) the sun is high . The difference between winter and summer coined the terms low and high solar path . For locations with the same geographical latitude , the same sun position diagram applies when using local solar time (true local time) as the time of day parameter.

With a sundial , instead of an axis diagram, an optical image ( representative geometry : gnomonic projection ) of the position of the sun is created. Its dial also contains sets of curves for certain equatorial coordinates , also in the form of daily hours or annual data , for the purpose of measuring time .

Observation of the position of the sun

Shadows cast on September 17th at noon in Singapore ; Sun at about the zenith .

The course of the daily position of the sun and its seasonal change is one of the earliest observations of the sky in human history. It was the basis of the astronomical worldview of antiquity and its direction and time measurements. Observation instruments were u. a. Protractor, the gnomon (shadow staff), the astrolabe and the armillary sphere .

Daily position of the sun (day arc)

The day arc of the sun is the part of its apparent daily orbit in the sky that runs above the horizon . The theoretical day arc begins with the astronomical rise and ends with the astronomical set. The actual sunrise or sunset takes place about 3–4 minutes earlier or later due to the refraction of light in the earth's atmosphere . The height of the landscape horizon (mountains, buildings) counteracts this - by around 6–8 minutes per degree.

The day arc begins between the polar circles on the eastern horizon and ends on the western. The motto

In the east the sun rises, in the south it takes its course, in the west it will set, in the north it can never be seen.

is only valid to a limited extent for the mean geographical latitudes between the tropics and the arctic circle in the northern hemisphere - for those in the southern hemisphere, south and north would have to be swapped. For lower latitudes between the tropics, it depends on the time of year whether the sun culminates in the south or north at noon. In Central Europe, the direction of the rises and sets can deviate by up to 45 ° from exactly east or west over the course of the year.

The moment of the meridian passage of the sun (almost its culmination ) is noon (more precisely: true noon ).

Seasonal position of the sun (change in height and length of the daily arc)

The day arc is higher and longer in summer than in winter. Its midday height at, for example, ± 50 ° latitude is 63.45 ° at the summer solstice and 16.55 ° at the winter solstice . Calculation: angle between pole and zenith of the location (90 ° minus latitude) ± inclination of the ecliptic; in the example around the year 2000: 90 ° - 50 ° ± 23.44 ° equals 63.44 ° and 16.56 °.

At the tropics , the sun is at its zenith once a year at noon (90 ° height), but twice between the tropics and at the equator. Beyond the polar circles , with the midnight sun and polar night in an annual rhythm, the effect occurs that the sun neither rises nor sets for a few weeks. Sun position diagrams for such locations extend over 24 hours or 360 ° azimuth.

The azimuth α for the location of sunrise or sunset varies over the year relative to the east or west point, for example at 50 ° latitude by ± 38.25 ° to the north or south. The hour angles for the moment of sunrise and sunset vary at locations of this latitude by ± 31.13 ° around λ = −90 ° (rise) or around λ = + 90 ° (set). The extreme lengths of the day (16 h 9 min or 7 h 51 min) differ accordingly by 4 · 31.13 ° · 4 min / ° = 8 h 18 min.

Effects of the position of the sun

Nature and man

A number of important variables depend on the position of the sun and its variability, above all

• the intensity of solar radiation . It also results from it
• the climatic zones (together with the humidity and cloud conditions ) and the types of vegetation
• the need for heating or cooling
• the development of local winds (see for example updraft ) and cloud formation , but also
• the shift of the earth's wind systems with the corresponding occurrence of regional winds (such as the monsoons ) and seasonal ocean currents
• (together with the slope of the terrain and shading by the horizon) the development of settlement structures , especially in the mountains
• (in interaction with the atmosphere - air, aerosol, precipitation) Color, UV intensity, brightness and lighting effect of direct and indirect sunlight (also the colors of the sky - even when the sun is below the horizon)
• Geometric light effects such as polarization through scattering on air molecules, rainbows , glitter of snow
• Propagation conditions for radio short waves due to changes in the ionosphere
• Energy generation in - possibly tracked - photovoltaics and solar thermal

Human culture

Measuring the position of the sun using sundials has enabled people to determine the time of day for thousands of years . The division into seasons corresponds to the daily arc height of the sun. The first determination of the diameter of the earth by Eratosthenes was carried out by simultaneously measuring the position of the sun at two different points on the earth's surface. Measuring the position of the sun with the help of simple measuring devices was also an early method of navigation .

The daily "path of the sun across the sky" plays a major role in various mythologies , for example in Helios ' "sun chariot" from ancient Greece and in the interpretation of sunrise and sunset . Residents of the northern hemisphere are often amazed at the "reversal" of the daily apparent movement of the sun "to the left" when they are in the southern hemisphere .

The fixed points of the sun's path that characterize the temperate zones of the seasons, such as the longest night ( beginning of winter ) or the longest day of the year ( beginning of summer ), as well as the equinoxes of the day and night at the beginning of spring and autumn, find diverse cultural and religious precipitation such as B. " Midsummer ", midsummer celebrations , Christmas etc.

Hour angle and analemma

Analemma figure: position of the sun over a year at the same mean local time

Until the end of the Middle Ages , the hour angle of the sun served as a measure of the time of day. It gives the hours before / after the local noon, which is why it bears this name.

Because the (apparent) movement of the sun over the course of the seasons is uneven for up to 15 minutes, the so-called equation of time was introduced for correction . It indicates by how much the true solar time has to be corrected in order to arrive at the uniform mean solar time . So is z. B. the moment of the meridian passage of the sun (almost its culmination ) the true noon , which is opposed to the "artificial" mean noon . Midday also deviates from the zone time (12 p.m. CET ) by a constant value, which results from the geographical difference in length to the zone meridian (for CET 15 ° east of Greenwich).

In sun position diagrams, the time scale is distorted in order to be able to read off the position of the true sun with a given mean solar time. Because the correction is different every season of the year, the true hour lines are not only shifted, but replaced by the typical double loops known as analemma .

Conversely, the time of day can be read from the position of the sun. The analemmas indicate the mean local time or, if shifted to the correct longitude, the zone time (in Central Europe CET ). When the sun position diagram is drawn on a spherical surface , the primary spherical coordinates hours and declination angle for the position of the sun are used. The situation on the celestial sphere is displayed realistically. In the Skaphe , an ancient sundial, a hollow sphere is the projection surface.

The sun position diagram can also be used to calculate the amount of sunshine in a building or the usable solar energy of a location. While the theoretical sunshine duration of each month only depends on the geographical latitude , the actual sunshine duration is also subject to meteorological influences (cloud cover, haze) and the height of the landscape horizon .

Astronomical connections

Representation in year diagrams

Simple sun position diagrams are parameterized with the true local time . The correction to mean local time is omitted. The angle of declination is assumed to be constant for the duration of the sunny day. Since the sun's paths hardly change from year to year, they can be used for many years. Parameterization with mean local or zone time is advantageous for practical use .

More precise determination of the position of the sun for a point in time

The influence of slow changes in the apparent path of the sun on the position of the sun at a point in time is taken into account as follows. The procedure is basically the same as for the more precise determination of the time equation . There is no approximation to the periodicity with the year. The position of the sun is determined in each case for a point on an axis of any length of uniformly passing time.

In contrast to the usual astronomical considerations (e.g. according to the planetary theory VSOP87 ), only the change in the course of the sun in the form of the shift of the vernal equinox towards the perigee of the earth's orbit ellipse is taken into account of the long-term influences .

Ecliptical coordinate of the sun

The number of days since the standard equinox J2000.0 (January 1, 2000, 12 noon DD ≈ 12 noon UT) is used as the time variable (including a fraction of the day in UT, if applicable ). ${\displaystyle n}$

If the Julian day number is the desired time, then applies ${\displaystyle JD}$

${\displaystyle n=JD-2451545{,}0}$.

The position of the sun on the ecliptic is initially determined without taking into account the speed fluctuations caused by the ellipticity of the earth's orbit . A mean speed of the sun is assumed (360 ° in approx. 365.2422 days) and the mean ecliptical length of the sun is obtained ${\displaystyle L}$ :

${\displaystyle L=280{,}460^{\circ }+0{,}9856474^{\circ }\cdot n}$.

In order to take into account the influence of the orbital ellipticity afterwards and to obtain the ecliptical length , the so-called midpoint equation must be added as a correction . This correction depends on the angle between the sun and the perihelion , called the anomaly . The midpoint equation expects the (fictitious) uniformly increasing mean anomaly as the input value . This increases by 360 ° in an anomalous year to about 365.2596 days: ${\displaystyle \Lambda }$ ${\displaystyle g}$

${\displaystyle g=357{,}528^{\circ }+0{,}9856003^{\circ }\cdot n}$.

The midpoint equation is a periodic function of the mean anomaly and can therefore be broken down into a Fourier series . In the case of small orbital eccentricities , the series can be terminated after a few terms. If only linear and quadratic terms are taken into account in the ( numerical ) eccentricity , the midpoint equation reads ${\displaystyle e}$

${\displaystyle \Lambda -L=\left(2e\sin(g)+{\frac {5}{4}}e^{2}\sin(2g)\right)\cdot {\frac {180^{\circ }}{\pi }}}$.

With and conversion, this results in the ecliptical length of the sun: ${\displaystyle e\approx 0{,}0167}$ ${\displaystyle \Lambda }$

${\displaystyle \Lambda =L+1{,}915^{\circ }\cdot \sin(g)+0{,}01997^{\circ }\cdot \sin(2g)}$.

Note: The statement is clear when you and brought by adding or subtracting suitable multiples of 360 ° in the range between 0 ° and 360 °. ${\displaystyle L}$ ${\displaystyle g}$

As an alternative to using the midpoint equation , the ecliptical length can also be determined from the mean length using the Kepler equation , which, however, requires an iterative solution method .

Equatorial coordinates of the sun

For the thus determined, ecliptical length counted along the ecliptic , the associated right ascension counted along the celestial equator must now be determined. With the obliqueness of the ecliptic ${\displaystyle \Lambda }$ ${\displaystyle \alpha }$ ${\displaystyle \varepsilon }$

${\displaystyle \varepsilon =23{,}439^{\circ }-0{,}0000004^{\circ }\cdot n}$

the right ascension results as. ${\displaystyle \alpha }$

${\displaystyle \alpha ={\begin{cases}\arctan \left(\cos(\varepsilon )\tan(\Lambda )\right),&{\text{wenn }}\cos(\Lambda )>0,\\\arctan \left(\cos(\varepsilon )\tan(\Lambda )\right)+4\,\arctan(1),&{\text{wenn }}\cos(\Lambda )<0.\end{cases}}}$

The case distinction ensures that it is in the same quadrant as (see position angle ). For computer programming, some programming languages ​​or environments include a function for this purpose, such as: B. . ${\displaystyle \alpha }$ ${\displaystyle \Lambda }$ ${\displaystyle \arctan 2(\varepsilon ,\Lambda )}$

As an alternative to the exact formula used here, a series expansion can also be used to determine , as is also possible with the equation of time. ${\displaystyle \alpha }$

The declination counted perpendicular to the celestial equator results as ${\displaystyle \delta }$

${\displaystyle \delta =\arcsin(\sin(\varepsilon )\sin(\Lambda ))}$.

Horizontal coordinates of the sun

The aim of determining the position of the sun for a certain point in time is the azimuth (direction of the compass) and the height of the sun. First, the hour angle of the sun is to be determined from the right ascension. ${\displaystyle a}$ ${\displaystyle h}$

To do this, determine the Julian day number for 0 ^h UT of the considered date, determine ${\displaystyle JD_{0}}$

${\displaystyle T_{0}\,=\,{\frac {JD_{0}-2451545{,}0}{36525}}}$in Julian centuries (each 36525 days) from J2000.0

and thus the mean sidereal time in Greenwich for the desired point in time (universal time UT, in hours): ${\displaystyle \theta _{G}}$ ${\displaystyle T}$

${\displaystyle \theta _{G}^{h}\,=\,6{,}697376+2400{,}05134\cdot T_{0}+1{,}002738\cdot T}$ in hours and fractions of an hour (i.e. 17.75 for 17:45).

The first term is the sidereal time of Greenwich at time J2000.0, the second describes the daily advance of sidereal time compared to the mean solar time by almost four minutes, the third adds the fraction of the day measured in sidereal time . The sidereal time is the hour angle of the vernal equinox , expressed in time measure ( ). Whole-number multiples of 24 ^hours can be deducted from the result if necessary. Multiplication by the conversion factor of 15 ° / h gives the Greenwich hour angle of the vernal equinox in degrees: ${\displaystyle 1^{\mathrm {h} }{\hat {=}}15^{\circ }}$

${\displaystyle \theta _{G}=\theta _{G}^{h}\cdot 15}$

For a place in longitude ( counting positively to the east ) the hour angle is the vernal equinox ${\displaystyle \lambda }$

${\displaystyle \theta \,=\,\theta _{G}+\lambda }$,

and subtracting the right ascension of the sun gives the hour angle of the sun for that location: ${\displaystyle \alpha }$ ${\displaystyle \tau }$

${\displaystyle \tau \,=\,\theta -\alpha }$.

The hour angle is set at 0 ° at the time of the highest point of the sun (12:00 p.m. true local time), and correspondingly −90 ° for 6:00 a.m. and + 90 ° for 6:00 p.m. true local time. The hour angle corresponds to the azimuth only at 12:00 noon, at all other times the azimuth must be calculated using the following formula.

Azimuth and elevation angles result with the latitude to ${\displaystyle a}$ ${\displaystyle h}$ ${\displaystyle \varphi }$

${\displaystyle a=\arctan \left({\frac {\sin(\tau )}{\cos(\tau )\sin(\varphi )-\tan(\delta )\cos(\varphi )}}\right)}$

respectively to

${\displaystyle h=\arcsin(\cos(\delta )\cos(\tau )\cos(\varphi )+\sin(\delta )\sin(\varphi ))}$.

Note: If the denominator in the arctangent argument has a value less than zero, 180 ° must be added to the result in order to bring the angle into the correct quadrant .

The determined azimuth is counted from the south . If it is to be counted from the north, add 180 ° to the result.

Correction of height due to refraction

Finally, if necessary, the refraction ( refraction of light in the atmosphere ) must be taken into account, which makes the solar disk appear slightly higher than it actually stands. The mean refraction (in arc minutes) for an object that is at height h (in degrees) can be calculated approximately using

${\displaystyle R={\frac {1{,}02}{\tan \left(h+{\frac {10{,}3}{h+5{,}11}}\right)}}}$.

The refractive height in degrees is then

${\displaystyle h_{R}=h+R/60}$.

It should be noted that the refraction depends on the detailed state of the atmosphere. The formula given assumes an air pressure of 1010 mbar and a temperature of 10 ° C. Conditions deviating from this can be taken into account by means of suitable corrections, but even then the formula only describes a mean refraction, while the actual values, especially in the immediate vicinity of the horizon, may differ significantly from this mean depending on the current temperature stratification.

example

The position of the sun is to be determined for August 6, 2006 at 8 a.m. CEST ( = 6 a.m. UT) in Munich ( = 48.1 ° N, = 11.6 ° E). It surrender ${\displaystyle T}$ ${\displaystyle \varphi }$ ${\displaystyle \lambda }$

${\displaystyle JD\,=2453953{,}75}$	${\displaystyle n\,=2408{,}75\,\mathrm {d} }$	${\displaystyle L\,=2654{,}638^{\circ }\,{\stackrel {\wedge }{=}}\,134{,}638^{\circ }}$
${\displaystyle g\,=2731{,}593^{\circ }\,{\stackrel {\wedge }{=}}\,211{,}593^{\circ }}$	${\displaystyle \Lambda \,=133{,}653^{\circ }}$	${\displaystyle \varepsilon \,=23{,}438^{\circ }}$
${\displaystyle \alpha \,=-43{,}881^{\circ }+180^{\circ }=136{,}119^{\circ }}$	${\displaystyle \delta \,=16{,}726^{\circ }}$	${\displaystyle JD_{0}\,=2453953{,}5}$
${\displaystyle T_{0}\,=0{,}06594113621}$	${\displaystyle \theta _{G}^{h}\,=170{,}9759^{\mathrm {h} }\,{\stackrel {\wedge }{=}}\,2{,}9759^{\mathrm {h} }}$	${\displaystyle \theta \,=56{,}239^{\circ }}$
${\displaystyle a\,=85{,}938^{\circ }+180^{\circ }=265{,}938^{\circ }\,{\stackrel {\wedge }{=}}\,-94{,}062^{\circ }}$	${\displaystyle h\,=19{,}062^{\circ }}$	${\displaystyle h_{R}\,=19{,}110^{\circ }}$

An astronomy program (SkyMap 2.2) provides for comparison , , and . ${\displaystyle \alpha =136{,}123^{\circ }}$ ${\displaystyle \delta =16{,}727^{\circ }}$ ${\displaystyle a=-94{,}065^{\circ }}$ ${\displaystyle h_{R}=19{,}106^{\circ }}$

Note: The calculations must be carried out with a sufficient number of digits (e.g. double precision , caution is advised with eight-digit pocket calculators); in particular for a sufficient number of positions must be considered. It should be noted that some computer programs and programming languages expect angles in radians and not in degrees ; the angles must then be converted accordingly. ${\displaystyle T_{0}}$

Accuracy comparison

The deviations between results from the literature ( JPL-Ephemeride DE405 ) and those of a similar simplified method shown here ( Astronomical Almanac ) almost always remain below 0.01 ° in the period from 1950 to 2050.

As the graphic opposite shows, the values ​​determined here for the position of the sun achieve an accuracy of around 0.01 ° in the period from 1950 to 2050. Most noticeable is the deviation in the ecliptical longitude with a regular period of 18.6 years and an amplitude of 0.0047 °; it is the nutation in length not taken into account in the present determination . The fluctuation range of the residual errors increases significantly towards the edges of the graphic. This is caused by the disregarded change in the eccentricity of the earth's orbit, which was set as constant with the value for the year 2000 when determining the coefficients of the midpoint equation. This error has the anomalous year as its period; its amplitude increases by 0.0048 ° in 100 years. Furthermore, those orbital disturbances that have a direct effect on the ecliptical length are neglected; especially the disturbances caused by Jupiter ( terms with amplitudes 0.0019 °, 0.0014 °, ...), moon (terms with amplitudes 0.0017 °, ...), Mars (terms with amplitudes 0.0014 °, 0.0011 ° , ...) and Venus (terms with amplitudes 0.0014 °, 0.0011 °, ...). The fact that the ecliptical latitude was tacitly set constant to zero does not produce a noticeable error. The determined coordinates and the comparison data apply to a geocentric observer; for a real observer on the earth's surface , the observed position of the sun can deviate from this by up to 0.0024 ° (the solar parallax ).

If more precise data is required, this can be determined with more complex procedures or obtained from one of the numerous ephemeris servers on the web (see web links).

Explanations

1. ↑ To do this, consider a fictitious, evenly moving sun, the so-called mean sun . It corresponds to a circular and not inclined earth orbit .
2. ↑ to the series expansion of the midpoint equation

Web links

Commons : Sun position diagrams  - collection of images, videos and audio files

• Current graph of the position of the sun for any location in Germany
• Calculation of sun position and twilight
• Current sun coordinates, hourly angles and sunrise / sunset for any location
• Ephemeris server at Calsky.com
• NASA ephemeris server

Libraries:

• Pysolar: staring directly at the sun since 2007
• Python & NOVAS Astrometry Software
• Libnova

swell

• Calculation by and : (Astronomical Almanac 2006), p. C24 ${\displaystyle \alpha }$ ${\displaystyle \delta }$
• Calculation of and : (Jean Meeus 2000), chap. 12, 13. The sidereal time formula shown here has been simplified due to the lower accuracy requirements compared to the original formula. The error remains smaller than 0.0001 ° in the period from 1950 to 2050, but increases quadratically outside these limits due to the neglect of a quadratic term. For the full formula, see the Sidereal Time article . ${\displaystyle A}$ ${\displaystyle h}$
• Refraction: (Jean Meeus 2000), chap. 16
• Error discussion of the simplified sun position calculation: Nutation (Jean Meeus 2000) Chap. 22; Disorders (TC Van Flandern, KF Pulkkinen 1979)
• Rise and fall: Definition, 16 '+ 34': (Meeus 2000), chap. 15th
• The Astronomical Almanac For The Year 2006 , The Stationery Office, London 2004, ISBN 0-11-887333-4
• Jean Meeus : Astronomical Algorithms . 2nd ed., 2nd printing. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1
• TC Van Flandern, KF Pulkkinen: Low-Precision Formulas for Planetary Positions . In: ApJ , 1979, Supp. 41, pp. 391-411, bibcode : 1979ApJS ... 41..391V