sunrise

Sunrise on the Simplon Pass (2018)

As sunrise is called both the passing ( rise ) of the horizon by the sun and the time of this event in the daily course of the sun and the celestial phenomenon altogether with all its (also meteorological ) phenomena.

term

On June 9th (? = 22.9 ° N) the sun rises in New Brighton (? = 45.0575 °) at an angle of 39.8 ° above the horizon

The sunrise follows the dawn , its opposite is the sunset . The cause of the phenomenon is the earth's rotation , which moves the viewer's place beyond the day-night boundary . In the sense of crossing the entire solar disk, it takes two minutes in the tropics , three to four minutes in Central Europe, depending on the season, several to many minutes in polar regions and more than a day at the poles.

The word sunrise refers to the human observer and thus to the geocentric worldview. In fact, the sun does not rise, but the position of the earthly observer turns towards the sun as a result of the earth's rotation.

From dawn to dawn based on the time-shifted vocal is songbirds an approximate determination of time possible (see bird watch ).

Astronomical Phenomenology

Peñón de Ifach ( Calpe ), Spain

Along with sunset , meridian passage and culmination, the rise is one of the most important aspects of astronomical phenomenology , which is why all astronomical calendars and yearbooks contain corresponding dates for the sun and moon . The calculation of such times is described in the article Visibility (Astronomy) . The times of sunrise and sunset in Germany are mostly related to the central town of Kassel and in Austria to the 15th degree of longitude . The local times deviate from this according to the true local time . For example, the sun rises around 35 minutes earlier in Cottbus than in Aachen .

Sunrise from Fondachelli-Fantina

Sunrise on a farm in Namibia (2014)

Because of the equation of time , the earliest sunrise does not coincide with the summer solstice , but occurs around June 17th. Analogously, the latest sunrise is not at the winter solstice (nowadays mostly on December 21st), but in northern Germany around December 29th, in Switzerland around January 3rd. The difference to the sunrise time on the day of the solstice is only about two minutes.

The time of the rising of the sun is defined as the moment when the top of the solar disk crosses the geocentric or true horizon ; if the upper edge falls below it, it is sunset.

From about ± 65 ° latitude (near the polar) and because of the curvature of the light rays in the earth's atmosphere caused by the astronomical refraction , only half the solar disk can exceed the true horizon at the time of the winter solstice. From about ± 67.41 °, the upper edge of the solar disk no longer reaches the true horizon (see also polar night ).

The apparent size of the sun varies between 31 ′ 28 ″ at the beginning of July and 32 ′ 32 ″ at the beginning of January, resulting in a deviation of approximately ± 1.7% over the course of the year. The Sun's mean apparent diameter is 31 '59.3 ". Due to the curvature of the light rays in the earth's atmosphere, the solar disk appears to have been lifted by about 0.6 °.

General projections cannot take into account the real horizon courses of specific locations and relate to an ideal mathematical horizon that is everywhere at the height of 0 °. For the calculation of such times see rise (astronomy) .

Azimuth of the sun at sunrise

Sunrise for different geographical latitudes at the beginning of summer in the northern hemisphere

Sunrise for different geographic latitudes at the beginning of winter in the northern hemisphere

The azimuth of the rising sun depends on the geographical latitude of the observer and the current declination of the sun , i.e. the season.

The azimuth of the rising sun can be calculated as a function of the latitude of the observer and the declination of the sun with the help of spherical trigonometry . On June 21 (beginning of summer in the N hemisphere) the sun is on the tropic and has a declination of 23.4 ° north. On September 23rd and March 21st, the sun is on the celestial equator and has a declination of 0 °. On December 21st (beginning of winter for the N hemisphere) the sun has a declination of 23.4 ° S. The azimuth of the rising sun is: ${\ displaystyle \ alpha}$ ${\ displaystyle \ varphi}$ ${\ displaystyle \ delta}$ ${\ displaystyle \ alpha _ {SR}}$

${\ displaystyle \ alpha _ {SR} = \ arccos \ left [{\ frac {\ sin (\ delta)} {\ cos (\ varphi)}} \ right]}$

The calculation of the azimuth of the sunrise shows, among other things, that at the beginning of winter on z. B. 80 ° north latitude the sun does not rise. For this latitude and the given declination of −23.4 °, the azimuth has no real value.

The steepness (angle ) with which the sun rises above the horizon at sunrise can be calculated for the different latitudes and the given declination as follows: ${\ displaystyle \ beta}$ ${\ displaystyle \ varphi}$ ${\ displaystyle \ delta}$

${\ displaystyle \ beta = \ arctan \ left [\ cot (\ varphi) {\ sqrt {1- \ sin ^ {2} (\ delta) \ sec ^ {2} (\ varphi)}} \ right] = \ arctan \ left [{\ frac {\ sin (\ alpha _ {SR})} {\ tan (\ varphi)}} \ right]}$

The graphic on the right shows that at the beginning of summer in the northern hemisphere (June 21), for an observer at 60 ° north latitude, the sun rises with an azimuth of 37 ° and rises clockwise over the horizon at a relatively flat angle of 19 °. For an observer at 20 ° north, the sun rises much steeper at an azimuth of 65 °, namely at an angle of 68 ° above the horizon. For this observer, the sun rising in the northeast runs eastwards and suddenly northwards later in the morning. For observers at the equator , the sun rises vertically at sunrise all year round. At the beginning of spring and autumn, the sun rises at an angle above the horizon in every place on earth . For example, on these two days at 40 ° latitude, the sun will rise at sunrise at an angle of 50 ° above the horizon. Both at the beginning of summer and winter , the sun will rise in the same place at sunrise at an angle of 45 °. ${\ displaystyle \ beta}$ ${\ displaystyle \ beta = (90 ^ {\ circ} - \ varphi)}$ ${\ displaystyle (\ delta = \ pm 23.4 ^ {\ circ})}$

The second graphic shows the azimuth of the sun and the steepness of the sun's path at sunrise on December 21 (beginning of winter in N) for observers at selected latitudes. Here, too, the sun rises vertically above the horizon for an observer at the equator.

Derivation of the formulas

Azimuth of the sun at sunrise

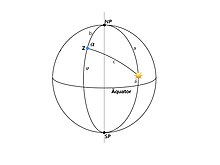
Spherical triangle on the celestial sphere

Steepness of sunrise

To calculate the azimuth of the sun at sunrise and to calculate the steepness with which the sun rises above the horizon at sunrise, consider the spherical triangle that is spanned by the three points north pole , zenith of the observer and position of the sun . In the graphic, Z denotes the zenith, NP the north pole, and SP the south pole. is the azimuth of the sun as seen from the observer. c is the zenith distance of the sun as seen from the observer. is the latitude of the observer and is the declination of the sun. ${\ displaystyle \ alpha}$ ${\ displaystyle \ varphi}$ ${\ displaystyle \ delta}$

The triangle shown is described with the spherical side cosine law:

${\ displaystyle \ cos (\ alpha) = {\ frac {\ cos (a) - \ cos (b) \ cos (c)} {\ sin (b) \ sin (c)}}}$

If you replace a , b and c with , and , where h is the height of the sun above the horizon, it follows: ${\ displaystyle a = 90 ^ {\ circ} - \ delta}$ ${\ displaystyle b = 90 ^ {\ circ} - \ varphi}$ ${\ displaystyle c = 90 ^ {\ circ} -h}$

${\ displaystyle \ alpha = \ arccos [\ sec (h) \ sec (\ varphi) (\ sin (\ delta) - \ sin (h) \ sin (\ varphi))]}$

At sunrise the sun is at the height h = 0 ° above the ground. With h = 0 ° the azimuth of the rising sun becomes:

${\ displaystyle \ alpha _ {SR} = \ arccos \ left [{\ frac {\ sin (\ delta)} {\ cos (\ varphi)}} \ right]}$

Steepness of sunrise

At sunrise the sun rises at an angle over the horizon. It is: ${\ displaystyle \ beta}$

${\ displaystyle \ tan (\ beta) = dh / d \ alpha = {\ frac {1} {d \ alpha / dh}}}$

The first derivation from to h at the point h = 0 gives: ${\ displaystyle \ alpha}$

${\ displaystyle \ tan (\ beta) = \ left [\ cot (\ varphi) {\ sqrt {1- \ sin ^ {2} (\ delta) \ sec ^ {2} (\ varphi)}} \ right] = {\ frac {\ sin (\ alpha _ {SR})} {\ tan (\ varphi)}}}$

The angle is positive when the sun rises from left to right, i.e. from east to south. If the sun rising in the east runs from right to left at sunrise, i.e. towards north, the angle is expressed negatively. ${\ displaystyle \ beta}$ ${\ displaystyle \ beta}$

Time dependence of the brightness

How the illuminance increases at dawn and how it progresses during sunrise can be easily captured by measuring the brightness . In addition to the purely phenomenological aspect, this is e.g. B. for biology and for the development of sunrise simulators (e.g. for use as light alarm clocks ) of importance.

The time dependence of the brightness in the period around sunrise depends heavily on the season, the weather and the latitude. If the sky is clear, the brightness can be estimated very well using an exponential function . The illuminance doubles every five minutes.

{\ displaystyle E = 80 ~ \ mathrm {lx} \ cdot 1 {,} 15 ^ {\ frac {t} {1 ~ \ mathrm {min}}} = 80 ~ \ mathrm {lx} \ cdot e ^ {\ frac {t} {7 {,} 16 ~ \ mathrm {min}}}}

${\ displaystyle E}$ is the illuminance and the time, where the time of sunrise is. is Euler's number . As a result, 10 lx ( lux ), which is roughly the illuminance of street lighting, is reached around 15 minutes before sunrise, and the brightness of average office lighting (around 800 lx) is exceeded around 16 minutes after sunrise. This formula is suitable for a period of one hour before to half an hour after sunrise (i.e. between −60 min and +30 min) for the latitude of Germany. The brightness increases faster in summer and slower in winter than indicated. ${\ displaystyle t}$ ${\ displaystyle t = 0}$ ${\ displaystyle e}$ ${\ displaystyle t}$