horizon
The horizon is a line that separates the sky from the earth .
In the case of the natural horizon, the course of this boundary line depends on the location and height of the observer as well as the local conditions of the surrounding landscape ; above the sea this line is also called the chimney . Observations that are dependent on the horizon, such as sunrise , can be compared more easily at different locations if they are related to a simplified horizon ( reference horizon ).

This ideal horizon spans a plane that is at right angles to the zenith or plumb direction and is referred to as the horizon plane or also the horizontal plane . A horizontal plane or line is often called a horizontal line .
The expression field of vision was introduced in the 17th century by Philipp von Zesen to mean a Germanization instead of horizon , but is only rarely used today with this meaning.
Word origin
The word horizon in German is a loan word from Latin , the Latin word horizon is borrowed from ancient Greek . It goes back to ὁρίζων horízōn with the meaning "border line" - as a shortening of the expression ὁρίζων κύκλος horízōn kýklos "limiting circle" or "the limiting circle" - formed to ὁρίζειν horízein "limit", a derivation of ὅρος hóros "limit".
Precise definitions

HH '- astronomical horizon
C 1 C 2 C 3 C 4 - nautical horizon
B 1 B 2 B 3 B 4 - optical horizon
The astronomical horizon is also circular; here it is shown as a straight line, as it appears to the viewer when looking in a certain direction.
Taking a closer look, there are some meanings to be distinguished, all of which differ in terms of their visibility and apparent distances to the horizon:
- Natural or landscape horizon : the boundary line between heaven and earth, as it depends on the local conditions ( landscape , mountains, city silhouette).
- Mathematical horizon or astronomical horizon : the line of intersection of the celestial sphere with the plane that is at right angles to the plumb line in the observation location . The latter, however, is not the direction from the observer to the center of the earth , but deviates from it by up to 0.2 ° because of earth flattening and deviation from the perpendicular .
- Nautical horizon , kim (ung), kink line : the natural horizon by the sea. Depending on the height of the observer, it is about the skin depth below the mathematical horizon.
- Optical horizon : the refraction of light in the air envelope ( terrestrial refraction ) increases the range of vision and the horizon is seen further away.
- Radio horizon : Radio waves behavesimilarly to light(depending on their wavelength , only from ultra-short waves onwardsone speaks of quasi-optical wave propagation ). The refraction is accounted for by a larger apparent earth diameter .
The horizon plane is the plane of the geometric horizon. The vertical to this plane cuts the celestial sphere in zenith and nadir .
Horizon in nautical science, chimney line
The notch is the visible boundary line between water and sky on the open sea . Measurements of elevation angles refer to them , for example with a sextant .
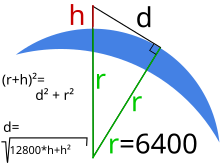
Because of the curvature of the earth - the mean radius of the earth is 6371 km, the radius of curvature of the earth is between a minimum of 6334 km and a maximum of 6400 km - the horizon appears lower below the mathematical horizon, the higher the observer is above sea level .
Therefore, the angle of elevation must be reduced by the depth of the skin . This so-called height loading is
(Knitting depth in arc minutes ; height of the observer in meters ).
According to DIN 13312 ("Navigation; terms, abbreviations ..."), the abbreviation " Kt ", in English the abbreviation " D " (from dip of horizon ), in aviation the abbreviation " Dip " should be used for the skin depth in seafaring become; The recommended symbol for seafaring is k .
The distance of the horizon from a point with the height above the surface of the earth can be calculated geometrically with the formula
calculate, where is the radius of curvature of the earth. If the value is used, which corresponds approximately to the maximum possible value in meters, the result for an observation height of 400 m is:
round
For heights that are much smaller than the Earth's radius is , the term can against be neglected; this gives the following approximation formula in simplified form
If you insert the mean earth radius (6.371 mm ) for , you get the horizon distance in kilometers, if the height is given in meters, with the rule of thumb :
This results, for example, for an observation height of 400 m:
The geometrically calculated distance to the nautical horizon does not correspond to the distance to the optical horizon because of the refraction of light in the earth's atmosphere . Depending on the pressure and temperature conditions in the lower air envelope, terrestrial refraction can fluctuate considerably. On average, the apparent radius of the earth is around 7680 km, the horizon seen around a tenth further away than the geometrically calculated one. The distance to the optical horizon can be estimated with the formula:, in the example
For details and additional examples see also geodetic visibility .
Horizon in math, astronomy and geodesy
The horizon in the mathematical sense is a great circle that divides the sphere or celestial sphere into two equal halves and whose pole is the zenith .
- Geometric horizon
- a great circle in the sense mentioned above, which has two points of reference in astronomy :
- Geocentric (True) Horizon: the horizontal plane goes through the
- Topocentric (apparent) horizon (more often used): through a location on the surface of the
earth , or through the position of the observer. The difference in the angle of elevation of a star corresponds to the parallax , while the azimuths are the same.
It is the basis of the horizon system - a coordinate system in which the stars and terrestrial measuring points are indicated by direction ( azimuth , course ) and elevation angle . The vertical circles , of which the meridian lies exactly in the north - south direction , run perpendicular to the horizon - i.e. through the zenith .
- Horizon as a reference
The horizon is the most important reference for local measurements. The most important devices for its realization are the spirit level or (more precisely) the tubular vial , furthermore height compensators and other pendulum bodies , electronic inclination sensors and sometimes liquid or mercury levels .
The horizontal is measured with a leveling device , the setting up of measuring instruments is called leveling .
Horizon in art

The term horizon is often used in art as a symbol for longings and utopias . Examples are the song Horizont by Udo Lindenberg , the novel The Lost Horizon by James Hilton or the picture Forgotten Horizon by Salvador Dalí . The horizon plays a central role in the works of the artist Jens Lausen .
In their song How far is it to the horizon, the Knorkator group addresses the calculation of the distance to the horizon using the Pythagorean theorem .
See also
- Dawn , sunrise , sunset
- Artificial horizon - measuring instrument for determining the horizontal
- Horizon problem, basic problem of cosmology
- Horizon astronomy
- Horizontal pendulum
- Horizon (geology)
literature
- Albrecht Koschorke : The story of the horizon. Boundaries and crossing of boundaries in literary landscapes. Suhrkamp, Frankfurt am Main 1990, ISBN 3-518-58064-7 .
Web links
References and comments
- ↑ see Duden online: field of vision
- ↑ compare Duden online: Horizont
- ^ Horizontis in the genitive , C. Lewis, C. Short: A Latin Dictionary. Oxford 1879, horizon .
- ↑ so also ὁρίζοντος κύκλος horízontos kýklos in Aristotle , see Liddell-Scott-Jones: A Greek-English Lexicon . 9th edition, Clarendon Press, Oxford 1940 [2003], ὁρίζων or keyword ὁρίζοντος , on Perseus .
- ↑ Kluge: Etymological dictionary of the German language . 23rd edition, Berlin 1995, p. 383.
- ↑ This approximation also applies to aircraft flying at an altitude of 10 km.