Equation of time

The time equation (ZG or ZGL) is the difference between the true solar time ( true local time , WOZ) and the mean solar time ( mean local time , MON):
This time difference arises when the true local time determined for a certain location - at which the sun at noon (12 o'clock WEC) is always above the same point on the horizon , the south point - is compared with a constructed time measure (MON), which is on refers to an averaged position of the sun over the course of the day. The differences result in part due to changes in web speed of the Earth in its orbit ( revolution ) around the sun on the elliptical orbit and on the other because of the revolution ( rotation ) of the earth on its axis , which is not perpendicular to the orbital plane and the annual Movement remains almost fixed in space:
- from the almost parallel shift of the inclined earth axis results - with approximately every six months - a periodic difference of about ± 10 minutes,
- The approximately elliptical shape of the earth's orbit results - with an approximately annual period - a periodic difference of about ± 7.5 minutes.
If the extremes of both periods coincided, the equation of time would have a maximum of + 17.5 minutes (+ 7.5 + 10) or a minimum of - 17.5 minutes (- 7.5 - 10). The annual extreme values are currently around +16 and around −14 minutes.
The equation of time changes steadily by up to about 30 seconds in 24 hours. In common tables, the value of the equation of time is given for each day of a certain year for the time 12:00 UT . For many applications it is sufficient to use this value anywhere on earth and for the entire local clear day.
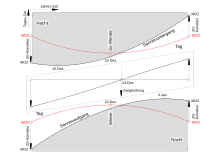
Most sundials show the true solar time and consequently are at times up to 16 minutes before or up to 14 minutes behind the mean solar time. A time equation table or diagram sometimes shown next to the dial helps the user work out the mean time (top picture). The true solar time of the 15th eastern longitude is often shown as a substitute for Central European Time ( CET) . The CET is obtained from such a sundial by correcting it with the value of the equation of time and the otherwise necessary correction from the mean local solar time of any degree of longitude to CET is saved.
The following diagram (picture below) is a little more than a year long excerpt from the equation of time (red line), which in principle runs steadily from the past into the future. There is no exactly the same annual course. However, the values that are four years apart (for example those for 2011 in the diagram and the future ones for 2015) only differ by seconds. Within the four-year switching period, due to the small shifts in the calendar day scale (<± 1 day) compared to the solar year , the annual sections coincide with slightly larger deviations, which are nevertheless smaller than ± 1 minute.
In astronomical yearbooks , the time equation values are recalculated every year, only provided for the year in question and given to the second. They can also take into account the latest findings on the influence of astronomical causes.

In addition, fictitious borderline cases can be seen: 1. without ecliptic skew , if the earth's axis were perpendicular to the earth's orbit (annual period); 2. on a circular orbit , if the earth moved on a circular orbit (half-yearly period).
Historical
The equation of time was already known to ancient astronomers. Geminos of Rhodes mentions them. In the Almagest of Ptolemy it was quite addressed accurately and concisely. Soon after Kepler's laws became known , John Flamsteed introduced the quantitative description in 1672.
In the older literature, the minuend and subtrahend are interchanged. This result with the opposite sign was added to the true solar time displayed on a sundial, which was previously used in everyday life, in order to obtain the mean solar time displayed with the newly invented wheel clock . This process corresponds to the old meaning of “equation” as “correction to be added”. This convention is still used in French yearbooks today.
Nowadays the mean time, which can be read from (in principle) constantly running clocks, has priority and the true solar time can be deduced from it. Today's sign regulation was made in order to be able to “correct” this habit.
Sidereal day, sunny day and mean sun
Sidereal day and sunny day

from 1 to 2 = a sidereal day
from 1 to 3 = a solar day
The time span between two meridian passages of the sun is a sunny day ; it is an average of 24 hours. In contrast to this, the time span between two meridian crossings of a fixed star is called a sidereal day . This corresponds to the duration for one rotation of the earth around itself and averages 23 hours 56 minutes and 4 seconds. The difference of an average of 3 minutes and 56 seconds to a sunny day results from the annual movement of the earth on its orbit around the sun . From day to day, the earth advances on the earth's orbit by almost one degree of arc (around 365 days of sunshine or around 366 sidereal days account for a full 360 degree rotation). Since rotation and rotation both have the same sense of rotation, the earth must continue to rotate by just under one degree beyond the full rotation until the sun goes through the same meridian again. These daily additional partial rotations make up exactly one complete rotation in a year. Therefore, the number of days related to the meridian passage of the sun is 1 less than that of the sidereal days.
The earth's rotation is very even, which is why the duration of a sidereal day fluctuates very little. In contrast, the fluctuations in the duration of sunny days are considerably greater because of the inclined axis of rotation of the earth and its different orbital speeds on the elliptical orbit around the sun. Sunny days can be up to about 30 seconds longer or up to about 20 seconds shorter than their mean value. Their differences from the mean can add up to around a quarter of an hour over a period of months before the effect is reversed again. The on Sun read off true solar time (LAT) thus passes uneven. Its deviation from the uniformly passing mean solar time (MONT), which can be read off, for example, from a wheel clock, is the so-called equation of time.
Middle sun
When the solar day "made" by the (apparent) movement of the (true) sun was recognized as being unevenly long, but the solar day was supposed to remain a basic measure of time, the formal use of a fictitious so-called mean sun was avoided and the so-called mean solar time was a uniform one Time measure created. The artificial mean sun of this model revolves evenly and not on the ecliptic , but on the celestial equator and "makes" the mean solar day .
Two causes of the equation of time, superimposed
The causes for the equation of time are easier to recognize from a heliocentric point of view, because they follow from the movements of the earth relative to the resting sun. For the sake of simplicity, the term “solar time” continues to be used occasionally, even if the movements of the earth, not those of the sun, are concerned as a function of time.
First cause: ellipticity of the earth's orbit
The orbit of the earth around the sun is an ellipse with the sun at one focal point. The second Kepler's law describes the change in the orbital speed of the earth during one orbit. In the vicinity of the perihelion - the point closest to the sun - the earth - seen from the sun - moves at a higher angular velocity than the average and covers a larger angle during one day, so that it has to make a slightly larger additional rotation until the sun returns goes through the meridian. That takes longer than average. In the vicinity of the Aphels - the point furthest from the sun - it is the other way round.
In the perihelion environment (winter half-year in the northern hemisphere), the true solar time passes more slowly because of the greater earth speed (and the resulting larger additional rotation), in aphelion environment (summer half-year in the northern hemisphere) it passes faster than the uniform mean solar time. The change in the true length of the day between two days is a maximum of approximately ± 8 seconds. The summation of these changes results in a maximum fluctuation of ± 7½ minutes in the true solar time within a year ( sine- like black line in the above diagram ( without ecliptic skew ), zero crossings in perihelion and aphelion).
The equation of time results from the fact that this fluctuation is still changed by the effect of the second cause.
Second cause: parallel displacement of the inclined earth axis
The direction of the earth's axis, which cuts the plane of the earth's orbit diagonally (not taken into account in the scheme shown above) with a deviation of about 23.44 ° from the normal , is almost unchangeable relative to the fixed stars. Viewed from the sun, the earth's axis changes its direction every day, it makes a full tumbling movement every year. The earth's daily travel by orbit is a rotation (approx. 1 °) around the orbit axis (or around the sun). The additional rotation of the earth required as a result takes place around its own axis. Since both axes are not parallel, both rotations are not equal.
At the equinoxes of the day and night , the two axes intersect when viewed from the sun at the angle ε ≈ 23.44 °. The cutting angle is now at its greatest. The rotation of the earth around its axis acts with maximum amplification as a rotation around the axis perpendicular to its orbital plane ( ecliptic ). The result is that the additional rotation and the time required for it are smaller than the average. The true solar time passes faster than the mean solar time.
Both axes seem to coincide at the solstices . One of the two poles of the earth is closer to the sun than the other. The daily 1 ° rotation of the earth around the orbit axis is shown as an arc on one of its two tropics . The corresponding arc on the earth's equator is larger. The required additional rotation of the earth around its axis and the time required for this are greater than the average. The true solar time passes more slowly than the mean solar time.
If the first cause of the equation of time were eliminated (fictitious borderline case), the change in the true length of the day between two days would be a maximum of about ± 20 seconds. The summation of these changes results within one year maximum of about ± 10 minutes semi-annual variation of the true solar time ( sinus -like magenta colored line in the diagram above: on circular path ; Start about the winter solstice).
Equation of time, superposition of two causes
The effects of the ellipticity of the earth's orbit and the parallel displacement of the inclined earth axis result in the equation of time. The two sine- like lines are approximations, and their relative phasing also changes slowly over time. The latter essentially causes the slow change in values of the basically four extreme values of the equation of time. The absolute maximum value of about | 17.5 | Because of the period ratio of 2: 1 of the two sine-like lines, min can only have one of the four extreme values. Positive / negative pairs of values are possible. Your two values can occur immediately one after the other (as is almost the case at the moment) or staggered in time (see also below in the section Analemma ).
The equation of time currently (2011) has the following parameters (see red line in the diagram above):
- Zero points: April 13th, June 13th, September 1st and December 25th,
- Main extreme values: February 11 (−14 min 14 s) and November 3 (+16 min 26 s) - an approximately identical pair of values.
- Secondary extreme values: on May 14th (+3 min 40 s) and on July 26th (−6 min 32 s) - another almost identical pair of values.
Negative numerical values mean: The true solar time follows the mean solar time or the true sun follows the mean sun.
Positive numerical values mean: The true solar time precedes the mean solar time or the true sun precedes the mean sun.
calculation
To determine a time equation value for a given point in time , the difference WOZ - MOZ ( see above ) can be traced back to the position of the sun and the position of a fictitious mean sun. The rotation of the earth around its polar axis is irrelevant.
Model of the mean suns
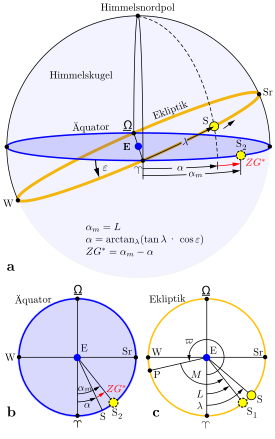
a celestial sphere
b equatorial section c ecliptical section,
angle spread The points on the ecliptic denote geocentric projections of the sun onto the celestial sphere at different times: ♈ and ♎ at the beginning of spring and autumn (point of spring or autumn); Sr and W at the beginning of summer or winter. S: early May. E: earth. P: perihelion. Other designations see text
Two fictitious mean suns are used to explain the equation of time (figure on the right). The first mean sun orbits uniformly with the mean angular velocity of the sun's orbit in the ecliptic and passes through the perihelion together with the true sun . The second mean sun revolves around the equator with the same period and happens at the same time as the vernal equinox ♈. is the mean or comparative sun with the right ascension
The equation of time results from this model
where the right ascension of the (true) sun denotes. The superscript asterisk indicates that the angle is shown instead of the time. If the true sun is west of the central sun, WOZ> MOZ , but . Therefore, the order of minuend and subtrahend is reversed compared to the initial definition by time difference.
During the day, the sun goes through 360 ° in 24 hours or 1 ° in 4 minutes. This applies to the equation of time in minutes
is to be entered in degrees. The angle and time formats of the equation of time are coincident versions of the same term.
Right ascension of the true and the comparative sun
| = | ||
| numerical eccentricity | ||
| = | ||
| Skew of the ecliptic in degrees | ||
| = | ||
| Length of the perihelion in degrees | ||
| = | ||
| mean length in degrees | ||
| = | Time from January 1st, 2000 12:00 UTC in days |
In the following, the right ascensions and for the point in time are determined. The calculation is based on Kepler's two-mass model , although here the earth is understood as the central body and the sun as the orbiting body. This is permissible because the geocentric position vector of the sun is exactly opposite to the heliocentric position vector of the earth (cf. sun path ). This means that Kepler's formula also applies to the apparent path of the sun (see also the position of the sun ).
To determine the right ascension of the sun , some elements of its apparent orbit around the earth are necessary. The values tabulated on the right are taken from Montenbruck. Montenbruck gives the orbital elements for the earth . Because the sun is the recirculating body here, the lengths and in the table are increased by 180 °.
The specified date for which the equation of time is to be calculated defines the time as specified in the last line of the table. This can be the mean anomaly of the apparent sun
can be determined from two path elements according to the table. The length of the true sun in the ecliptic
results from a series expansion of the midpoint equation
with sufficient accuracy. The midpoint equation describes the apparent movement of the sun ( orbit ellipse of the earth) with the same result as the solution determined from the Kepler equation.
The right ascension of the sun depends on its ecliptical length via the transformation formula
from ecliptical to equatorial coordinates (skewness see table). The index at arctan calls up the (secondary) value of the arctangent relation that is closest (see arctangent with position parameter ).
In order to synchronize the orbit of the second central sun with that of the first in the manner described by Schneider (see above) , the central right ascension must be assigned the time course of the solar orbit element (see table). With
all sizes for the calculation of and are available.
result
Starting with , the previous information leads to the summarizing formula
which deals with a tangent addition theorem in
can be formed.
Components
The equation of time function can be calculated according to
composed of two components. The left term quantifies the contribution of the orbital eccentricity (“first case”, see above) with the earth's axis perpendicular to the ecliptic ( ). From Eq. follows for it
This part runs like a sinus with an annual period. The values are equal to those of the negative midpoint equation . The two zeros coincide with the apses .
The right summand represents the contribution to the eccentricity unrecognized by the obliquity of the ecliptic is added ( "second Usache", supra). He surrenders to
and also runs like a sine, but with two periods per year. The four zeros coincide with the beginning of the season .
Duration and accuracy
The equation of time formula with the tabulated constants can be used several centuries before and after the year 2000. The values deviate by less than 5 s from those of an exact reference model (e.g. VSOP ) which - unlike the Kepler model - takes into account the disruptive forces of the other planets and especially the moon.
Numerical example
The table contains the values in the order of the calculation steps without rounding the intermediate results. The celestial sphere graphic fits roughly at the selected time.
| value | 5599.125 d | 0.016703 | 23.437 ° | 283.204 ° | 5799.228 ° | 5516.025 ° | 1.704 ° | 5800.932 ° | 5798.508 ° |
| Main value | 39.228 ° | 116.025 ° | 40.932 ° | 38.508 ° | |||||
| value | 0.720 ° | 2.88 min | -1.704 ° | -6.82 min | 2.424 ° | 9.70 min |
A precise comparison value for is 2.89 min.
Equation of time values for the passage of marked orbital points
The calculation of time equation values for the passage of marked path points is shorter and simpler. There is no need for the time-consuming and inconclusive determination of a railway location belonging to a given time. The Kepler equation is recommended for this calculation .
Sunrise and sunset at the time of the solstice
The fact that the sunset occurs several days before the winter solstice again later in the evening and the sunrise only several days later earlier in the morning is a consequence of the equation of time. In WOZ, the boundaries between night and day and between day and night are symmetrical to one another over the date axis, but not in MON. After correcting the WOZ using the equation of time for the MOZ, the daily corridor (see adjacent figure) is distorted. The turning points of its boundary lines have shifted to an earlier date (sunset) or to a later date (sunrise).
This has no noticeable effect on the date for the shortest day of the year (winter solstice). It remains around December 22nd (1-day variation due to leap year cycle ).
The same effect exists at the summer solstice. It is less pronounced than in winter because the slope of the equation of time as a function of the date is only about a third as great.
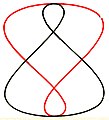
Analemma
If the dependence of the equation of time on the declination of the sun is shown as a diagram, a loop shape is created, which is called an analemma. This loop shows the true position of the sun at 12 noon mean local time for the different seasons as the height above the celestial equator and as the lateral distance from the meridian. In the lateral direction, four minutes of time correspond to one degree in angular measure. The figures shown on the left apply north of the Tropic of Capricorn with the direction of view to the south. In the pictures on the left, the figures are stretched by a factor of five to six in the horizontal direction compared to the sky figure. On the right you can see the corresponding shadow curve (left / right undistorted analemma) marked on a vertical wall in a historical noon time .
The slight asymmetry between right and left is due to the fact that perihelion and winter solstice do not fall on the same day. The latter was last the case in 1246 (day of the winter solstice roughly like today). The inner interface applied approximately to April 16 and August 29 ( Gregorian calendar applied backwards).
In the year 6433 perihelion will have reached the equinox of spring . The equation of time will be zero on the days of the equinoxes and the analemma will be a figure symmetrical about that point.
Most often, the analemma is seen as an hourly loop on sundials, which are designed to indicate the mean solar time. Often, however, it is divided into two parts (one part similar to an S, the other similar to a question mark) to avoid confusion when reading (there are two points on the whole figure for a declination value). Each of the two parts is valid for about half a year. Such watches have two interchangeable dials. The dials can easily be designed for the zone time valid at the place of installation , ie they show the "normal time".
The sun, photographed at the same mean time every day, adds up to an analemma in the sky.
Analemma , 20./21. century
Analemma , schematically
black in 1246, red about 11,620Analemma , schematically
red in the year 6433, black approx. 16,810
literature
- Hughes, DW, Yallop, BD, Hohenkerk, CY: The Equation of Time , Mon. Not. R. astr. Soc. (1989), 238 , 1529-1535 ( bibcode : 1989MNRAS.238.1529H )
- Bernd Loibl: When is noon? In: Stars and Space . Spectrum of Science, 8–9 / 1996. Pp. 643-645.
- Robert Weber. Time systems. In: Hermann Mucke (Hrsg.): Modern astronomical phenomenology. 20th Sternfreunde Seminar, 1992/93. Planetarium of the City of Vienna - Zeiss Planetarium of the City of Vienna - Zeiss Planetarium and Austrian Astronomical Association 1992, pp. 55–102.
Web links
- Qualitative treatment with pictures
- Qualitative treatment, good explanation
- Approximation formula
- Elementary treatment → annual equation as the sum of 2 sine functions
- classical treatment → no annual equation ( Memento from April 7, 2014 in the Internet Archive )
- With mathematics (series developments) → annual equation as the sum of 4 sine functions
- Demanding mathematical treatment (differential and integral arithmetic) → annual equation as the sum of 10 sine functions
- Equation of time calculation for 1800–2200
Notes and individual references
- ↑ The scale is designed for CET , so the true solar time displayed for 15 ° East (true local time WOZ) is corrected to mean solar time (mean local time MOZ) for 15 ° East (equal to CET). Location: 12 ° 22 'East, scale shift: about 10½ minutes (corresponds to the angle between the vertical and the XII o'clock line).
- ↑ a b There are also modern sundials that are designed to compensate for time. Cf. Siegfried Wetzel: The physics of the sundial. In: Writings of the historical-scientific group of friends of old clocks in the German Society for Chronometry. Deutsche Gesellschaft für Chronometrie (Ed.), 1998, ISBN 3-923422-16-4 , Figures 16 to 18 ( online , PDF ).
- ^ O. Neugebauer: A History of Ancient Mathematical Astronomy , Berlin 1975
- ^ R. Wolf: Handbuch der Astronomie , Amsterdam 1973
- ↑ Flamsteed began his career with an important treatise on the determination of the equation of time. [1]
- ↑ Flamsteed J .: De inaequilitate dierum solarium dissertatio astronomica. London 1672. ( online )
- ↑ N. Dershowitz, EM Reingold: Calendrical Calculations . Cambridge University Press, 2008, ISBN 978-0-521-70238-6 , pp. 182 .
- ↑ J. Meeus: Astronomical Algorithms , Richmond 2000, p. 184
- ↑ In most cases the observation site is not on the reference longitude of the used zone time , which therefore differs from its mean local time. You have to determine the latter in advance: Potsdam is z. B. 2 ° west than 15 ° east, the reference longitude of the CET . The mean local time is 8 minutes (4 minutes / longitude difference) less than the CET displayed by the (wrist) watch.
- ^ Siegfried Wetzel The equation of time, treated in an elementary way - DGC-Mitteilungen No. 109, 2007
- ↑ When calculating the equation of time in the first approximations, the acceleration of the earth periodically caused by the moon is neglected. For example, one currently calculates for the passage of the perihelion on January 3rd or 4th (difference within a four-year switching period), which, strictly speaking, only applies to the common center of gravity of the earth and moon. Only with the desired accuracy in the seconds range is taken into account that the center of gravity of the earth rotates around the common center of gravity on a radius of about 4700 km, i.e. the earth is temporarily up to 4 700 km ahead or back in the orbit direction during a lunar period.
- ↑ Siegfried Wetzel The equation of time, treated in an elementary way - DGC-Mitteilungen No. 109, 2007: The values given follow in a simple manner from the specifications 23.44 ° deviation of the earth's axis from the perpendicularity to the plane of the orbit ( inclination of the ecliptic ) and 236 seconds to that the mean solar day is longer than the sidereal day.
- ↑ The four seasons would be exactly the same length and therefore the calendar dates of the zero crossings (solstices and equinoxes) would be postponed to about two days.
- ↑ Manfred Schneider: Himmelsmechanik, Volume II: Systemmodelle , BI-Wissenschaftsverlag, 1993, p. 507, ISBN 3-411-15981-2
- ^ J. Meeus: Astronomical Algorithms , Willmann-Bell Richmond 1998/2009, Chapter 25: Solar Coordinates
- ^ O. Montenbruck: Basics of the ephemeris calculation , Spectrum Academic Publishing House Heidelberg, 7th edition 2005
- ↑ Orbital elements
- ↑ Center equation , s. There also a note on the origin of the midpoint equation
- ↑ derivation of the reduction from the Schneiderian model (s graphic. Equation of time as the angle ): The time the spring point of passage in the ecliptic follows from to . and are the constants given in the Path elements table . The right ascension of in the equator is to be applied as a linear equation . Since the orbital period of the two mean suns should be the same, the following applies . The two central suns go through the vernal equinox together, which leads to the equation . With it follows . The settlement thus fulfills the characteristics of Schneider's equation of time model.
- ^ M. Schneider: Himmelsmechanik, Volume II: Systemmodelle , BI-Wissenschaftsverlag, 1993, p. 508, ISBN 3-411-15981-2
- ↑ after Multiyear Interactive Computer Almanac 1800 - 2050 , US Naval Observatory, Willmann-Bell 2005
- ↑ Heinz Schilt: To calculate the mean time for sundials , Writings of the Friends of Old Clocks, 1990
- ↑ Analemmas photographed in the sky in Greece [2]






















![{\ displaystyle C = {\ frac {180} {\ pi}} \ left [\ left (2e - {\ frac {e ^ {3}} {4}} \ right) \ sin M + {\ frac {5} {4}} e ^ {2} \ sin (2M) + {\ frac {13} {12}} e ^ {3} \ sin (3M) + \ dots \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09230197a645e899170a97f5d81fa5b30c9ca5bd)