sundial

The title of this article is ambiguous. See also: Almtaler sundial , mountain region.

Vertical sundial with pole rod , south wall, rod shadow turning to the left

Antique sundial (cut off scaphe ) with nodus (tip of a lost horizontal rod)

Equatorial ring sundial with Bernhardt roller (front edge shadow to display the time)

A sundial is using the matter of the sun in the sky, the time of day to. The line-shaped sun shadow of a stick usually serves as a pointer . During the day, the shadow rotates around the attachment point of the rod on the dial scaled with the hours of the day . The variety of executed sundials is based primarily on the different shape and orientation of the dial. The most common variant is the vertical sundial with a flat dial, often on a building wall.

Sundials have been in use since ancient times and were mostly meant when people talked about clocks at the beginning of the 19th century . Until the beginning of the 20th century, they were still used, limited to the display of the noon hour (so-called noon clock), to adjust mechanical clocks that were still too imprecise. Today they are often only used as decoration on buildings, in gardens and in parks. Modern sundials with a relatively elaborate design - for example with a Bernhardt roller or the Helios sundial  - are able to display the "official" time in all seasons to display the minute exactly, for example CET or CEST .

On some sundials, the length of the rod shadow is also used to roughly indicate the calendar date : on a vertical sundial, the shadow is long in spring and summer and short in autumn and winter .

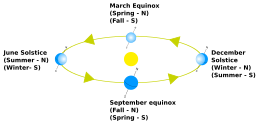
The position of the sun in the sky

Sun on the celestial sphere (above, reduced)
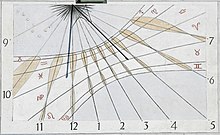
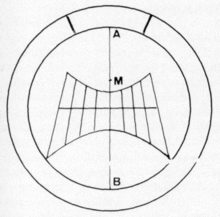
Image of the sun as a shadow point ( gnomonic projection ) or as a shadow line on the sundial dial (below, enlarged)
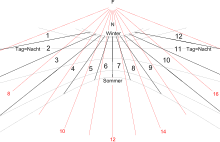
Hour lines gray and blue; Daily lines: green, red and cyan

Sun trajectories on the celestial sphere : front summer solstice , rear winter solstice , middle day-night-same
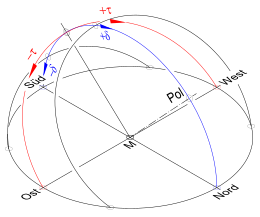
angle coordinates, hour angle and declination angle ${\displaystyle \tau }$ ${\displaystyle \delta }$

The sum of all possible places of the sun in the sky (position of the sun) is half of the surface area of ​​a half layer of the celestial sphere bounded by the horizon and the two tropics . In the east and west, the horizon limits the course of the day of the sun, which can be specified with the variable hour angle (figure on the left, above). The annual movement of the sun takes place between the tropics and is indicated with its variable declination angle.

The two angles that indicate the position of the sun (figure on the right) can be interpreted separately:

• the hour angle as time of day and ${\displaystyle \tau }$
• the declination angle as the calendar date. ${\displaystyle \delta }$

Function of a sundial

Illustration of the sun as a shadow

A shadow- casting point ( nodus ) creates a shadow point from the sun. The sun and sky (representing the circles imagined on it) are depicted in a central projection (as with the camera) - here in the so-called gnomonic projection - two-dimensionally on the dial (figure on the left, below; the dial can in principle have any shape and orientation) . Two coordinate values ​​are sufficient to specify the position of a point in a plane. Conversely: In the position of the shadow point, the values ​​of the two angular coordinates that characterize the location of the sun on the celestial sphere are coded. The decoding takes place with the help of the line network from the imaginary circles of the sky:

• The radial lines differentiate the hour angle, they are scaled with daily hours (in Central Europe 16 lines for 16-hour days in midsummer).
• The hyperbolas differentiate between the declination angle, they are scaled with calendar data (traditionally 6 hyperbolas and 1 straight line for 12 calendar days in the year, 5 lines used twice for 2 calendar days each).

Theoretically, the center M of the celestial sphere is the center of the earth. However, the node positioned in M ​​may be a little above the surface of the earth without any noticeable error. The celestial sphere with the distance to the sun as the radius is so large compared to the earth that any place in, on or near the earth can be considered its center.

When using a shadow-throwing stick ( pole stick , as it points to the celestial poles), the display of the calendar day is eliminated. The advantage is that the resulting line-shaped bar shadow is more conspicuous and recognizable more quickly than the shadow point. The principle of the projection corresponds to the image with a cylindrical lens . A point (the sun) is depicted as a line (shadow line) one-dimensional. The shadow stick must be in the celestial axis, in which all imaginary hour circles on the celestial sphere intersect. It is thus correctly aligned for the mapping of all hour circles to hour lines. The pole shadow falls at the same time of day on the same day line regardless of which day of the year it is. During the day it rotates around the intersection of the radial hour lines (base point of the pole rod) and falls on a scaled hour line after every hour.

The reversal of the image using light instead of shadow also occurs in sundials. Point light is generated by a pinhole (like a pinhole camera ) and line light is generated by a slit.

Values ​​of hour and declination angles

The earth's axis does not change direction during the year

The apparent daily movement of the sun around the earth takes place approximately on a circle on the celestial sphere . The time it takes for a complete orbit is the sunny day (also civil day or calendar day ). One of the 24 equally long ( equinoctial ) hours of the full day corresponds to the movement of the sun over 15 ° (360 ° ÷ 24 = 15 °). On the horizontal sundial dial, the angles between the hour lines deviate from 15 ° (the mean of 12 intermediate angles symmetrically distributed over the hour line of true noon is 15 °).

The sun culminates in summer at noon 2 × 23.5 ° higher above the southern point (northern hemisphere of the earth) of the horizon than in winter. The decisive factor for the annually changing culmination is that the earth's axis, which is inclined at 23.5 ° to the earth's orbit, does not rotate around the sun , but rather maintains its direction relative to the stars during the sun's orbit ( eccentric movement , adjacent figure). The sun seems to move in a different parallel circle in the sky every day . On the sundial dial, these are depicted as hyperbolic calendar day lines from the point casting the shadow.

Comparison between the node and pole rod principle

In antiquity , the two-dimensional display by means of nodus was common and necessary, because the temporal hours to be displayed and changing with the season are a function of both the hour angle and the declination angle. The point of a vertical staff, the gnomon , which gave the field of gnomonics its name, served as the nodus . A central projection with the projecting point in the middle of the body to be imaged is therefore generally referred to as a gnomonic projection.

In the late Middle Ages the mechanical clocks were invented, which brought the constant equinox hours independent of the season to prevail in public use. A one-dimensional illustration with a pole stick is sufficient to display this type of hour on a sundial. The shadow line is easier to read in relation to the hour lines on the dial than the shadow point of the Nodus. In addition, like the pointer of a mechanical watch, it rotates around a point (the base of the stick). These are the reasons why sundials with a pole rod are more common than those with a nodus.

The nodus was actually no longer needed after the transition to the equinox, but was still used alongside the pole rod. Modern sundials, which take into account the so-called equation of time in the display, again need the point display, because this "equation" is a function of the season.

Time of day display

The actual function of a sundial is to display the time of day. Compared to the mechanical and electronic clocks commonly used, the sundial is quite "wrong" because the apparent movement of the sun is not uniform. Until the invention of the mechanical clock at the end of the Middle Ages, this "mistake" was of no importance. One could easily accept that the true solar time over the year deviated from the evenly running time in the summer half-year by about ± 5 minutes, in the winter half-year even by about ± 15 minutes. The general public had no knowledge of this. That would have been of no use either, because there was no better continuously measuring clock than the sundial. Only astronomers knew about the uneven course of the sun and corrected the measured solar time ( true solar time ) with the so-called equation of time , which Ptolemy already knew, to the uniformly passing time ( mean solar time ) in order to make their observations more interpretable.

The time measured with an ordinary sundial differs from that measured in places with a different geographic longitude . It is called the true local time of the installation location (only the same in locations with the same degree of longitude). However, some sundials are not scaled for the true local time at the installation site, but rather for the true local time at the reference longitude of the legally applied zone time , e.g. B. for the true local time on the 15th longitude east (CET) or on the 30th longitude east (CEST). This display deviates from the zone time - the mean local time at the reference meridian - by the equation of time. Sundials with correction of the equation of time are relatively rare because the construction required for them is complex.

Vertical sundial for equinoctial hours
above: LAT (X II to pm), middle: CET
below: EDT (10 to 18 pm, numbers above the other)
MEZ- and CEST display error with the equation of time vitiated

vertical sundial for the mean local time in Munich (not CET )

In the following descriptions, the following distinguishing features are taken into account when measuring the time of day using a sundial:

• the duration of the differently defined hours,
• the start of counting for the differently defined hours,
• the fluctuation during the year to be compensated for with the equation of time.

In this way, the hours displayed on the still existing historical sundials, which are defined differently than today, and the modern correction for the display of the evenly running time (mean solar time) are included.

Display in equinox hours

The equinox hours, which have been in effect since the end of the Middle Ages until today, can advantageously be displayed as true local time (WOZ) when using a pole stick (line-shaped shadow). The scale can also be displayed for the WOZ of the reference meridian of the time zone (image: vertical sundial for equinoctial hours ), which, however, fluctuates over the year against the official time. Modern sundials with applied equation of time again need the historically older nodus for display.

Display of the mean time of day

Sundials that apply the equation of time have e.g. B. instead of straight hour lines shaped like an analemma , on which the hour is displayed with the help of a shadow spot (picture: vertical sundial for mean local time in Munich ). To enable confusion-free reading, the analemma loop is often divided into two parts and attached to two dials, which are exchanged twice a year. Another possibility is to double the sundial, whereby each half-sundial is provided with one half of the analemma loop (see the picture below of a cylindrical sundial for mean local time (MOZ) ). Such clocks are mostly used for measuring the zone time (for example CET and / or CEST).

Display in temporal hours

Vertical dial for temporal hours ; for comparison: in red for equinox hours

Vertical sundial for Italian hours

In the case of the temporal hours of the day used in antiquity, the length depends on the season (parameter: solar declination). The clear day, which varies over the year, is divided into twelve equal hours. The equation of time “error” is always included, because the reference point is the middle of the day, which fluctuates over the year and results from the times for sunrise and sunset.

Temporal hours can only be displayed with punctiform shadows on a two-dimensional scale. On the dial in the picture Vertical dial for temporal hours , equinox hour lines drawn in red, on which the shadow of a pole rod falls, are drawn for comparison. This goes through the Nodus N and its base point F on the dial. The nodus is in front of the dial. The lines for temporal hours are only approximate straight lines and do not intersect at a point. Their parts indicating the summer are more distant from one another than those of the equinox hour lines. It's the other way around in winter. Both clusters of lines intersect on the days of equinox .

Display in special hours

During the transition from temporal to equinox hours there was the use of equinox hours, which were not related to the highest point of the sun ( true noon ), but to the sunrise or sunset. Both moments vary over the year, which is why these hours can only be displayed with a point shadow. Such hours were Italian hours (from sunset), Babylonian hours (from sunrise) and Nuremberg hours (from evening with gradually changing counting start).

Display of the year date

The declination of the sun is a direct measure of the date of the year. A sundial with nodus records the day orbit (date lines) of the sun. Traditionally, the days at the beginning of the twelve astrological signs of the zodiac are selected. Since the declination hardly changes during a day, five lines of the summer half year ( Leo to Sagittarius ) can also be used in the winter half year ( Aquarius to Gemini ). Together with the lines for the solstice days (the beginning of Cancer and Capricorn ), a dial contains seven date lines (hyperbolas in the images, vertical sundial for mean local time in Munich and vertical dial for temporal hours ).

The dials

Sundial (scaphe) with nodus

Cylindrical sundial for MOZ, above: first, below: second half of the year

Equatorial sundial

The basic differentiating criterion for sundials is the use of either a pole rod or a nodus . Otherwise they differ mainly in the shape and orientation of their dial . All shapes and all orientations in space are possible. The following three forms are the most common. The list leads from the most complex to the simple form and at the same time from the historically oldest to the form that predominates today.

Spherical dial

This dial is the opposite of the celestial sphere. It was already used in antiquity under the term scaphe (picture at the beginning of the article) and was provided with lines for temporal hours. The modern version in the picture opposite is lined for equinox hours. The non-indicating parts are cut off from the hemisphere of a scaphe.

On globe sundials , the dial is on the outside of a sphere. A modern globe sundial with Nodus in the middle is the Helios sundial .

Cylindrical dial

Because a cylindrical surface is easier to manufacture than a spherical surface, hollow cylinder sundials (see picture opposite) and hollow cone sundials were the successors of the ancient scaphe.

A cylinder sundial used as an elevation sundial has its scale on the outside of a cylinder (also known as a column sundial).

Flat dial

Most sundials have the simple flat dial, which is also usually attached to a house wall. In the case of horizontal sundials , it is on the floor, sometimes on the top of a pedestal or on a table.

Horizontal sundials have the advantage over vertical sundials that they are always sunny between sunrise and sunset. Vertical sundials cannot show the early and late hours of the day in summer. If it is not a pure south (house) wall, the restriction is greatest in the morning or in the evening.

The dial of the equatorial sundial (see adjacent picture) has a special orientation. It lies in the plane of the celestial equator. Such a sundial has a dial on both sides of the dial (above for the summer half-year; below for the winter half-year). On the days of the equinox, the clock cannot be read due to grazing light.

Another special orientation of the dial is the position parallel to the pole rod on a polar sundial . The hour lines on the dial are parallel lines. The polar east sundial is located on a wall facing east. The polar west sundial is the counterpart to this. Between these two boundary alignments, the polar dial is located on a south wall tilted backwards.

history

Gnomon

The observation of the shadow length of a vertically extended object - a gnomon  - is the beginning of the time measurement with a sundial. Man probably started with it in his earliest history, using himself as a shadow thrower. Reliable sources for this come from ancient Greece in the form of tables on which the time of day is given depending on the length of the shadow. Such tables ( shadow tables ) were used later in the Roman Empire and still in the Middle Ages. The length of one's own foot was used as the unit of measurement.

With a staff as a gnomon a noon wise man was created , one of the first astronomical instruments. With the help of a scale placed on the floor in the meridian direction, the shadow length at noon was determined as a measure of the season. If the season is known, Eratosthenes , who had the earth as early as 240 BC, has B.C. as a sphere, can determine the radius of the earth fairly precisely from the midday shadow of two equal midday wise men. There was a noon wiser in Syene - today's Aswan - and one in Alexandria . The measurements were taken simultaneously on the day of the summer solstice . To do this, he evaluated the difference in elevation angles of the sun, which are contained in the shadow lengths, and the known distance between the two locations.

An application of the gnomon took place early in the Indian circle , which actually only determines the cardinal points. This gnomon application could therefore also be helpful early on for prefabricated sundials, because these have to be set up according to the cardinal points so that they function properly as a timepiece.

In Osireion described Egyptian sundial

Discus in plano ( Vitruvius )

Canonical sundial

Polygonal sundial

Portable ring sundial

Oldest sundials

When the shadow was finally measured at any time of day on a scale extending on both sides of the noon line, a full-fledged sundial was created. Only a few texts exist on this early step, taken independently of one another by the Sumerians in various ancient cultures such as China and Mesopotamia . The first well-documented archaeological finds of sundials come from ancient Egypt in the 13th century BC. Chr.

The ancient Egyptian sundial (picture: ancient Egyptian sundial described in the Osireion ), for example also in a variant as a wall sundial , used a horizontal shadow projector. The position of such a shadow always (except on the equator) depends on the date of the year, which is why these clocks are only considered primitive forerunners of sundials that are in principle correctly constructed. A sundial with a horizontal rod in a wall was used again in the Middle Ages as a canonical sundial (image: canonical sundial ).

Vitruvius describes around 10 BC In the ninth of his ten books on architecture the antique sundials known to him. The list begins with a sundial from the third century BC. Chr. Living Chaldean Berossus and scaphe of living at the same time Aristarchus of Samos . In both cases it is a hollow sphere sundial. Berossos first used a complete hemisphere, which he called a hemispherium . He had created a complete counterpart to the visible part of the celestial sphere. Later he limited himself to something more than the scaled part and gave this watch the name Hemicyclum . Aristarchus chose the name Skaphe , which is still used today for all hollow-sphere sundials .

In Vitruvius' list follows the discus in plano by Aristarchus, presumably a horizontal sundial, one of which was found on the Via Appia (image: discus in plano ). Then follows the arachne of the somewhat older Eudoxos of Knidos from the 4th century BC. The rest of the sundials mentioned by Vitruvius could not be found or interpreted.

In the first century BC The octagonal Tower of the Winds in Athens was built around the corner and has vertical sundials all around . They are the largest antique vertical clocks. In addition to the sundial usually attached to a south wall, there are seven other sundials, each pointing in a different direction.

The Roman emperor Augustus had in 10 BC Set up an obelisk from Egypt as a gnomon on the Field of Mars in Rome . However, this only served as a noon clock and calendar (display of the length of the shadow at noon containing the season). The fact that the so-called Solarium Augusti was a complete sundial did not turn out to be a realistic assumption.

Canonical sundial

After the end of the Roman Empire, the use and manufacture of sundials declined. The knowledge about it was almost lost. Since the eighth century AD, simple sundials similar to the wall sundials in ancient Egypt were made again. The name they are now using canonical sundials indicates their use in monasteries and their surroundings. They were used to remember the prayers to be performed during the day, which have been strictly regulated since Benedict of Nursia (photo: canonical sundial ). It was accepted that the prayer times indicated by such an imperfect sundial were neither evenly distributed over the day nor independent of the season. The spread of this type went hand in hand with the missionary activity of the Benedictines from Ireland and England .

Sundial with pole rod

After the Crusades , the pole rod appeared in Europe , with which the sundial achieved its fundamental perfection, if one disregards the fact that the true local time it indicates is still subject to the error of the equation of time . The pole rod is first described in the 12th century by the Arab Abul Hassan al Marrakushi , which indicates that it is an Arab invention.

Modern sundials

The sundial has been an object of art and mathematics since the Renaissance . For example, lavish multi-faceted sundials were created for stately terraces and parks .

Portable sundials have since appeared in a variety of forms. Most often there were so-called folding sundials, in which when opening a cover between the base plate with scale (horizontal sundial) and it a thread is stretched as a pole rod. They also carry a magnetic compass , with the help of which the orientation within the cardinal points is made. Furthermore, were cup sundials in use.

→ Main article : Portable sundial

Sundials remained indispensable until the end of the 19th century. Only then did mechanical clocks achieve sufficient accuracy and reliability that they no longer had to be corrected every noon, for example at train stations, with the aid of a noon clock corrected to midday .

Today, sundials can again be found more and more in private gardens, on houses and in public parks - mainly in countries whose culture has its roots in Greek and Roman antiquity . There are also new monumental sundials, for example the large floor sundial on the Hoheward dump between Herten and Recklinghausen .

Summary: A multiple vertical sundial

The multiple sundial from Santuari de Lluc (Mallorca) is described in more detail below, as it summarizes the development of the sundial and its different uses using four selected examples. The sundial is on the longitude λ = 2 ° 53 ′ east (see middle dial, above). The true local time there is about twelve minutes ahead of that in Greenwich , the true local time at 15 ° East (reference longitude for the Central European Time valid in Spain) about 48 minutes.

1. Canonical sundial (top left)

The night prayers are also noted on the dial, although only the times between sunrise (PRIMA) and sunset (VESPERAE) can be displayed. Only noon (SEXTA) can be accurately displayed as the time of the passage of the center of the sun through the meridian. The picture will soon show an hour in the afternoon, which is the time for the NONA prayer.

2. Sundial for Babylonian hours (bottom left)

The shadow thrower is the tip of the staff ( Nodus ). Below are counted from sunrise equinoctial hours. The dial also contains the seven date lines for the twelve time periods, which are marked with the astrological signs of the zodiac . In the picture, the nodus falls around the ninth hour after sunrise. It is August / September (Virgo zodiac sign) or March / April (Aries zodiac sign).

3.Sundial for true local time (WOZ) (center)

The display takes place both with a pole rod (upper sheet metal edge) and with a nodus, the intersection of the sheet metal edge with a small cross bar on it. The mode is only required to display the season. The face of this watch is not made wide enough to contain the shadow of the Nodus at the time of day of the picture. The pole rod edge shows about 20 minutes after 2 o'clock in the afternoon as WOZ.

The numbers to the left and right of the sun mean:

λ = 2 ° 53 ′ E and φ = 39 ° 50 ′ N: geographical coordinates of the location

−11 ′ 32 ″ (G): Time difference between WOZ at the location and WOZ on the 15th longitude east

δ = 13 ° 48 ′ E: angle by which the vertical wall is rotated from the south to the east.

4. Sundials for Central European Time (CET and CEST) (right)

The shadow object is again a rod tip (node), with which the equation of time can be taken into account. The upper sundial is used in the summer half-year, the lower one in the winter half-year. This enabled the analemma-shaped hour lines to be divided into two halves that could be read without confusion. Both clocks are scaled for CET (upper digits for CET, lower digits for CEST). The display shows around 4:10 a.m. CEST (afternoon, upper clock).
Check with the 2:20 o'clock display on the middle clock: 2:20 + 48 min (corresponds to a longitude difference of 15 ° - 2 ° 53 ′) + 60 min (difference between normal and summer time) ≈ 4:10 a.m.

The astrological date lines are an addition to the approximate reading of the season.

Sayings and inscriptions

Sayings and other inscriptions on sundials originated very early. Most of them have already been written in Latin. Some have a reference to the measurement of time, such as Horas non numero nisi serenas (literally: I don't count the hours if they are not cheerful), who says “Do it like the sundial, just count the cheerful hours” is the most common sundial saying today. Others are very general considerations about time and life, such as: Tempus fugit (“Time flies.”) Or Vita in motu (“Life is in motion.”).

See also

• Sunshine autograph - similar in structure, for recording the duration of sunshine
• Star clock
• Earth orbit
• Erich Pollähne , sundial builder

literature

• Ernst Zinner: German and Dutch astronomical instruments of the 11th-18th centuries Century , Beck'sche Verlagsbuchhandlung, Munich 1956; Unchanged reprint 1979, ISBN 3-406-03301-6 .
• René RJ Rohr: The sundial. History, theory, function , Callwey, Munich 1982, ISBN 3-7667-0610-1 (comprehensive and illustrated presentation).
• Wolfgang Zäck: Sundials in the Eifel : Typology and spatiotemporal differentiation . 1987, DNB 212982559 (Dissertation A University of Bonn, Faculty of Mathematics and Natural Sciences, 1987, 203 pages).
• Hugo Philipp, Daniel Roth, Willy Bachmann: Sundials - Germany and Switzerland. Deutsche Gesellschaft für Chronometrie, Stuttgart 1994, ISBN 3-923422-12-1 (directory of the fixed sundials in Germany and Switzerland).
• Karlheinz Schaldach: Roman Sundials , Frankfurt am Main 2001, ISBN 3-8171-1649-7 .
• Arnold Zenkert: The fascination of the sundial . 5th edition. Harri Deutsch, Thun / Frankfurt am Main 2005, ISBN 3-8171-1752-3 .
• Karlheinz Schaldach: The ancient sundials of Greece. Frankfurt am Main 2006, ISBN 3-8171-1756-6 .
• Jürgen Hamel : Inventory of the historical sundials in Mecklenburg-Western Pomerania (= Acta Historica Astronomiae 34). Harri Deutsch, Frankfurt am Main 2007, ISBN 3-8171-1806-6 .
• Karl Schwarzinger: Catalog of the fixed sundials in Austria. Austrian Astronomical Association, 2011.
• Ulrike Feist: Sun, Moon and Venus: Visualizations of Astronomical Knowledge in Early Modern Rome (= Actus et Imago , Volume 10). Akademie-Verlag, Berlin 2013, ISBN 978-3-05-006365-2 (Dissertation University of Augsburg 2011, 259 pages).

Web links

Commons : Sundials  - Collection of images, videos, and audio files

Commons : Sundials in a systematic overview (variety of sundials in one overview)  - album with pictures, videos and audio files

Wiktionary: Sundial  - explanations of meanings, word origins, synonyms, translations

Wikisource: Sundial  - Sources and full texts

• Karl Schwarzinger: Gnomonics. June 25, 2006, archived from the original on January 15, 2013 ; accessed on February 10, 2019 . 
• Frans (W.) Maes: Sundial Site. Retrieved August 8, 2012 .  - Nijmegen, 1999/2008, updated July 2013, last accessed 14 January 2016. Images of 200 sundials, including 50 analemmatic; Theory - (Dutch, English)
• Siegfried Wetzel: Essays on Sundials. Retrieved August 8, 2012 . 
• "Sundials" map of Germany from ZEITmagazin, October 26, 2016

Individual evidence

1. ^ Karl Schwarzinger: Catalog of the fixed sundials in Austria. Austrian Astronomical Association, 2006, p. 21.
2. ^ Karl Schwarzinger: Catalog of the fixed sundials in Austria. Austrian Astronomical Association, CD from 2011: around 3500 out of 3800 sundials are vertical sundials.
3. ↑ See Bassermann-Jordan / Bertele: Uhren. Verlag Klinkhardt & Biermann, 1961, p. 101.
4. ^ Siegfried Wetzel: The physics of the sundial. In: German Society for Chronometrie (ed.): Writings of the historical-scientific expert group Friends of old watches in the German Society for Chronometrie. 1998, ISBN 3-923422-16-4 , pp. 177-188, Fig. 10 ( online , PDF ).
5. ^ Siegfried Wetzel: The physics of the sundial. In: German Society for Chronometrie (ed.): Writings of the historical-scientific expert group Friends of old watches in the German Society for Chronometrie. 1998, ISBN 3-923422-16-4 , pp. 177–188, Fig. 12.2 ( online , PDF ).
6. ↑ Conversely: The model for the rotating pointer of mechanical clocks is probably the rotating shadow of the pole rod.
7. ↑ Even today's sundials often use the silhouette of the pole tip for seasonal information. Their dials contain date lines as well as hour lines.
8. ^ Hugo Michnik: Contributions to the theory of sundials. Supplement to the annual report of the royal high school in Beuthen O.-S. for the school year 1913/14, p. 3.
9. ^ Heinz Schumacher: Sundials , Volume 1. Callwey, 1973, ISBN 3-7667-0279-3 , p. 178.
10. ^ Arnold Zenkert: Fascination Sundial. 2nd Edition. Verlag Harri Deutsch, 1995, ISBN 3-8171-1386-2 , p. 39.
11. ^ Arnold Zenkert: Fascination Sundial. 2nd Edition. Verlag Harri Deutsch, 1995, ISBN 3-8171-1386-2 , p. 41.
12. ^ Karlheinz Schaldach: The ancient sundials of Greece , Frankfurt am Main, 2006, ISBN 3-8171-1756-6 , p. 23
13. ↑ Such a table and most of the following information on the history of the sundial can be found in: René RJ Rohr: The sundial. Beginnings and development of the sundial. Callwey, 1982, ISBN 3-7667-0610-1 , pp. 10-30.
14. ↑ Ludwig Borchardt: Ancient Egyptian time measurement in The History of Time Measurement and Clocks , Volume I, Delivery B, edited by Ernst von Bassermann-Jordan, 1920
15. ^ Vitruvii de architectura libri decem. / Vitruvius. Ten books on architecture . Translated and annotated by Curt Fensterbusch. Primus Verlag, Darmstadt 1996, ISBN 3-89678-005-0 .
16. ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 23.
17. ↑ Arachne means spider , probably an indication that this clock, like the younger discus in plano , was provided with declination lines.
18. ^ Karlheinz Schaldach: The ancient sundials of Greece. Frankfurt am Main 2006, p. 68.
19. ↑ Michael Schütz: On the sundial of Augustus on the Marsfeld. In Gymnasium 97 (1990), ISSN  0342-5231 , pp. 432-445; s. a. Solarium Augusti
20. ↑ Frans W. Maes: The sundial of the emperor Augustus: rise and fall of a hypothesis. In: Deutsche Gesellschaft für Chronometrie, annual publication 2005, ISBN 3-89870-255-3 , pp. 168-184.
21. ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , pp. 26-27.
22. ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , pp. 27-28.
23. ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 29.
24. ↑ Ralf Kern: Scientific instruments in their time . Volume 1. Walther König, Cologne 2010, ISBN 978-3-86560-772-0 , p. 426ff.
25. ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 30.
26. ^ Karl Schwarzinger: Sundials (Fig. 41). Retrieved August 8, 2012 . 
27. ↑ The data on the photo reveal September 9 as the observation date
28. ↑ Harald Hartmann: Sundial sayings and their meaning. Retrieved August 8, 2012 . 
29. ↑ (for beginners, with construction instructions and an additional 250 annotated pictures of sundials on CD-Rom)