Analemmatic sundial

Special feature: additional displays of azimuth (angle scale on the stick base) and elevation angle (adjustable device on the stick)

The analemmatic sundial belongs to the category of azimuthal sundials .
use
The common version has an elliptical dial on the bottom . A vertical shadow rod is positioned on the small axis of the ellipse, depending on the season ( declination of the sun). It is particularly popular that the user can act as a shadow thrower himself. The time of day is displayed as the true local time from the intersection of the rod shadow and the elliptical scale.
history
The oldest analemmatic sundial is in front of the former Brou monastery near Bourg-en-Bresse (France). It is possible that this clock was erected at the same time as the monastery at the beginning of the 16th century. The scale for setting up the shadow stick in the form of an analemma loop is a "technical error" and probably originated from a later restorer, because this scale is basically a straight line.
The first known theoretical treatment comes from the French mathematician Jean-Louis Vaulezard in Traictè ou Usage du Quadrant analematique , Paris 1640, in which he also claims to be its inventor. This form of a sundial was also dealt with by the English astronomer Samuel Foster in his 1654 (posthumously, because died 1652) work Elliptical or Azimuthal Horologiography . Foster also developed a variant that is better known under the name of the later living mathematician Johann Heinrich Lambert .
In the 18th century there were portable double sundials consisting of an analemmatic and a clock with a pole rod that did not need a compass for orientation . After that, however, the analemmatic sundial was forgotten. Today you can find it as a popular floor sundial, executed like its old model from Brou , in many parks and in many public places.
Explanation of name and function
Name: Analemmatic sundial
Vaulezard was a mathematician who mainly worked on geometry. His sundial must be viewed as an application of the geometric curve ellipse. He called his construction method Annalemme , which eventually became the name of the sundial that was preserved. The construction method is the analemma of Vitruvius , who used it to depict celestial circles in the plane as ellipses. At that time, the appropriate term orthogonal projection did not yet exist.
Name: Azimuthal sundial
A vertical shadow bar shows the azimuth of the sun directly on the horizontal plane . From this follows the name azimuthal sundial as a generic term for sundials set up in this way. In addition to the analemmatic sundial, they also include the sundial spider . Because of its more frequent occurrence, “ the azimuthal sundial ” is often understood to mean the analemmatic sundial alone.
function
The structure and function of an analemmatic sundial can be derived from a ring-shaped equatorial sundial .
The ellipse of an analemmatic floor sundial with a vertical shadow stick is the vertical parallel projection of the equatorial ring. The fixed pole rod of the equatorial sundial, which is parallel to the roof, becomes the shadow rod to be set up on the ground depending on the season. The indicating point on the ellipse is the shadow of a variable node contained in the vertical bar. During the day it rises up in it until noon, then down again to its foot. The rod points upwards to the nodus in the pole rod of the circular equatorial sundial imagined above, which is effective for approximately one day. In their pole rod the nodus only wanders back and forth over the year. This migration corresponds to the shift of the rod of the analemmatic ground sundial along the north-south axis (minor axis of the ellipse) over the year. In contrast to a sundial with a pole rod, the sun is depicted two-dimensionally in an analemmatic sundial .
Variants and geometric generalization
Like Vaulezard , other mathematicians found some variants of the sundial described above for purely geometric considerations. One of them is the sundial, which can be found again today, after the Englishman Samuel Foster and the Alsatian Johann Heinrich Lambert . With it, the celestial equator or the ring of an equatorial sundial can also be imagined in parallel projection, but not vertically on a horizontal plane. If the projection direction has an angle of (90 ° + φ) / 2 to the north point of the horizon or (90 ° -φ) / 2 to the south point (φ = geographical latitude), a circle is created instead of an ellipse. With a corresponding sundial, the hour lines are evenly distributed like on a flat equatorial sundial. The shadow bar , which is also to be set, has the slope of the projection direction. The term azimuthal sundial no longer applies, because the inherent coordinate system is twisted around the east-west axis. In the Foster-Lambert sundial shown opposite, the shadow stick is inclined to the north.
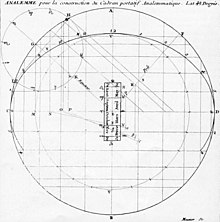
As a travel sundial (north-north with compass), the Vaulezard version has several ellipses (all with identical focal points) on the dial, which apply to different latitudes. It can be used as a solar compass if one knows the time of day, and was used for this purpose and under this name in the African campaigns on both sides of the Second World War .
A broader geometric generalization is that celestial circles or their equivalents in sundials are projected in some way onto the horizontal plane. As a result, there are so-called astrolabe sundials that use the stereographic projection , which is also the basis of the astrolabe . Historical examples come from the German Peter Apian (1495–1552) and the Englishman William Oughtred (1574–1660).
literature
- Rene RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1
- Louis Janin: History and Development of the Analemmatic Sundial. In: watch technology. No. 2, 1974, ISSN 0720-9614 , pp. 1-15.
Web links
Notes and individual references
- ^ Siegfried Wetzel: A mathematical description of the analemmatic sundial
- ^ Rene RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 118
- ^ Rene RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 120
- ^ Rene RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 124
- ↑ Bedos de Celles: La Gnomonique pratique. Paris 1780
- ↑ Armin Zenner: About the Analemma , German Society for Chronometrie, Yearbook 2000: Das Analemma ... in the 17th century by F. d'Aiguillon named "Orthogonale Projektion".
- ^ Siegfried Wetzel: Model of an equatorial and an analemmatic sundial
- ^ Rene RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1 , pp. 124-127
- ↑ Heinz Schilt: A sundial as a compass ... , writings of the friends of old clocks, 1992, pp. 192–200, Fig. 3
- ^ Rene RJ Rohr: Der Lambert'sche Kreis , Writings of the Friends of Old Watches, 1989, p. 131
- ^ Rene RJ Rohr: Astrolabische Sonnenuhren , Schriften der Freunde old Uhren, 1979, pp. 83-90

