Vertical angle
Vertical angles are angles measured in a perpendicular plane . In geodesy and astrometry , they describe in particular all angles related to the perpendicular direction .
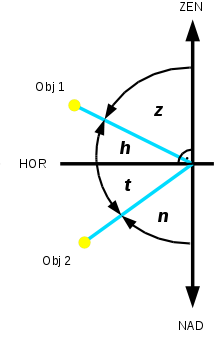
If the zenith , the nadir and the horizon are selected as the starting point, the following four vertical angles can be defined:
- Zenith angle (also zenith distance, zenith distance ): as the angle of a point below the zenith;
- Altitude angle (also height, elevation, altitude ): as the angle of a point above the horizon;
- Depth angle (also depression angle): as the angle of a point below the horizon;
- Nadir angle: as the angle above the nadir (the point opposite the zenith).
The following applies: ,
Elevation angle and depth angle correspond to the viewing angle between the line of sight and the horizon. The zenith angle and nadir angle correspond to the viewing angle between the line of sight and the plumb line.
units
Vertical angles are often given in astronomy in degrees or sexagesimally in degree- minutes - seconds (° ′ ″), while in geodesy gons are used. In the military and in ballistics , the " line " is also used as an angle unit (6400¯ = 360 °), because it makes distance measurement easier (the sine of 1¯ is almost exactly 0.001).
Types of angles
Elevation angle
An elevation angle is the angle of a point over a reference surface (such as the horizon ). In astronomy, it is also known for short as altitude . In geodesy, however , height refers to the perpendicular distance from the reference surface.
The height measurements with dragonflies or pendulum-compensated instruments relate to the “mathematical horizon”, which is realized by the plumb line, ie without taking into account the actual appearance of the horizon (shaped e.g. by vegetation, buildings and mountains). In seafaring, the usual sextants were used to measure the heights of the sun or stars above the chimney , which is the apparent dividing line between sea and sky. The skin depth must then be subtracted from the measurement in order to obtain the elevation angle.
Depth angle
A depth angle is the angle of a point below the horizon.
It is used like the elevation angle, but for cases where the observer is higher than the object. In this case the elevation angle has a negative sign , but the depth angle has a positive sign . The following applies to objects below the horizon .
The depth angle is sometimes referred to as the depression angle. It is to be distinguished from the angle of inclination, which describes the inclination of a device with respect to the perpendicular direction and can be both positive and negative.
Zenith angle
The zenith angle or the zenith distance is the angle between a target point and the perpendicular direction . Formerly the zenith angle was also called the “vertical angle”, but this is avoided today due to the misunderstanding of the term.
Using zenith angles as opposed to elevation and depth angles has several advantages:
- Zenith angles do not need a sign because they are always between 0 ° and 180 ° (between 0 ° and 90 ° for objects above the horizon and between 90 ° and 180 ° for objects below the horizon).
- The reference to the vertical axis of the measuring instrument is direct (the usual formulas also apply to inclined measuring axes, e.g. in mechanical engineering )
- The zenith is clearly defined, while the reference to the "horizon" can mean the mathematical one, but also the nautical horizon, a gyro - or the landscape horizon.
- Most measuring devices use the zenith angle as the output vertical angle.
Nadir angle
Nadir angles are mainly used in remote sensing and photogrammetry . The angle to the nadir for aerial photographs is ideally around 0 °, since deviations from the nadir that are too great cause image distortions and make the orthogonal recording unusable. For points close to the horizon, the nadir angle directed to the horizon is 90 °.
use
Vertical angle are used for the determination of heights , the geographic coordinates , for measurement of terrestrial objects and positions, and in astronomy to calibration of celestial bodies .
Use in astronomy
The elevation angle of a celestial body is called astronomical height (also German Altitude ); it is usually referred to as. The height of a star can be between + 90 ° (the zenith) and −90 ° (the nadir), with a positive height indicating that the object is above the horizon, while a negative height means that the object is below the horizon .
Together with the azimuth , the height forms a topocentric horizontal coordinate system or, more generally, an azimuthal coordinate system .
Use in geodesy
In geodesy , the use of vertical angles is limited to two, as they can be clearly determined for their starting position:
- Zenith angle (or ): as the angle of a point below the zenith ;
- Elevation angle (or ): as the angle of a point above or below the horizon , where the sign determines the direction;
The following applies: .
In geodesy, a depth angle is usually expressed by an elevation angle with a negative sign. The nadir angle is also replaced by the supplementary zenith angle.
Measurement
Directional reference
A measured vertical angle relates to the true perpendicular direction - also known as the astronomical perpendicular direction - and thus to the natural coordinate system . However, a geodetically calculated vertical angle can also refer to the normal of the earth ellipsoid at the measuring point. With the true perpendicular (which is based on the geoid and thus on the measurable gravitational field of the earth), this includes the perpendicular deviation . It can be around 10 ″ in the hill country, but it can reach 30–60 ″ in the high mountains.
Realization of the directional reference
The reference of the measuring device to the exact direction of plumb bob is created by a level or a plumbing sensor . The latter a liquid compensator in the optical path of the can riflescope be, or a small pendulum body in the reading optic . In technology and navigation , gyro platforms are also measured.
Measuring device
The most important instruments for vertical angle measurements are classified according to their measurement accuracy :
- Zenitteleskop and Photographic Zenitteleskop as well
- Zenith cameras , meridian circle and passage instrument (± 0.01 ... 0.1 ″)
- Theodolite and total station (depending on the purpose ± 0.5 ... 10 ″)
- Plumbing instruments and inclinometers ; for nautical height measurements also sextants (± 0.5… 5 ′)
- Protractors and direction finders (± 0.2… 1 °).
- Astrolabe , the navigation device of the early seafarers, approx. ± 0.5 °.
corrections
For accuracies higher than one arc minute , the measured vertical angle must be reduced by the influence of height index errors and refraction :
- The height index error is the deviation of the zero direction of the instrument from the plumb direction or from the horizontal. It is determined with the height circle vial or (for newer theodolites) with an inclination sensor .
- Every measurement within the earth's atmosphere is influenced by refraction. If the light beam runs entirely within the atmosphere, one speaks of terrestrial refraction .
- If, on the other hand, a star or an earth satellite is measured, the curvature of light is called satellite or astronomical refraction . At a zenith angle it is about 1 ′ (55–65 ″) and for stars close to the horizon up to 0.6 ° (33–40 ′). The terrestrial refraction, however, is given in fractions of the earth's curvature and amounts to an average of 0.13 of the earth's radius . However, it can also have negative values near the ground (especially in summer ).
- For special purposes of earth measurement and land surveying, a reduction must also be made due to the influence of the vertical deviation (up to 50 ").
See also
literature
- Emil Bachmann: Surveying for engineers and technicians . Archimedes-Verlag, Kreuzlingen, 1950.
- Hans Volquardts and Karl Matthews: Surveying . 26th edition, VIII, BG Teubner, Stuttgart, 1985.
- Bertold Witte and Hubert Schmidt: Surveying and the basics of statistics for the construction industry . P. 250, Volume 17, 4th edition, Konrad Wittwer Verlag, Stuttgart, 2000.
- Walter Großmann and Heribert Kahmen : surveying . 12th edition, De Gruyter-Verlag, Berlin and New York 1988.
- Heribert Kahmen: Surveyors . 18./20. Edition, De Gruyter-Verlag Berlin 1993 and 2005.
- Wolfgang Torge : Geodesy . 2nd edition, de Gruyter-Verlag, Berlin 1975.
- Industrieverlag: Taschenbuch der Navigation . Karlheinz Gehölsen GmbH, Heidelberg ~ 1967.
- Hilmar Ingensand: Introduction to geodetic measurement technology . Institute for Geodesy and Photogrammetry ETH Zurich, Zurich 2012.
Individual evidence
- ^ Hans Volquardts and Karl Matthews: Surveying (Part 2) . 14th edition, VIII, pp. 7-8, BG Teubner, Stuttgart, 1981.
- ^ A b Hans Volquardts and Karl Matthews: Surveying (part 2) . 14th edition, VIII, p. 7, BG Teubner, Stuttgart, 1981.
- ^ Walter Großmann and Heribert Kahmen : Surveying . 12th edition, III, pp. 13-33, De Gruyter-Verlag, Berlin and New York 1988.
- ↑ a b c Bertold Witte and Hubert Schmidt: Surveying and basics of statistics for the construction industry . P. 250, Volume 17, 4th edition, Konrad Wittwer Verlag, Stuttgart, 2000.
- ^ A b Hilmar Ingensand: Introduction to geodetic measurement technology . Pp. 79–82, Institute for Geodesy and Photogrammetry, ETH Zurich, Zurich 2012.