Astronomical refraction

from Wikipedia, the free encyclopedia
Astronomical refraction: The light beam (yellow) appears to be raised, compared to the vacuum, the zenith angle is reduced by r ( z = z '- r ). With satellites, the refraction is less important because of the shorter beam.
Terrestrial refraction : sunset over the Aegean Sea, magnified approximately 10 times. Without refraction, the sun would be 120% of its diameter lower. The left edge of the sun shows a small refraction anomaly .

Astronomical refraction is the change in direction of a light beam falling from the outside onto the earth by refraction in the atmosphere . The cause is the increase in the refractive index from n = 1 in the vacuum of space to around n = 1,00029 on the ground. Astronomical refraction is a special case of terrestrial refraction .

The curvature of the light rays takes place downwards - in the same sense as the curvature of the earth , but much less. The strongest curvature occurs near the ground and makes up a maximum of 10-15% of the earth's curvature in very flat sights .

At sea ​​level and expressed in terms of angles, the astronomical refraction is depending on the temperature

  • about 0.6 degrees (34 ' to 39') for horizontally incident light rays - that is at the up or sinking of a star,
  • about 29 ′ at half a degree above the horizon,
  • about 5 ′ at an elevation angle of 10 °,
  • about 1 '(55 " to 65") at an elevation of 45 °
  • and zero at a perpendicular angle of incidence - i.e. at the zenith .
  • It follows a complicated formula with several atmospheric parameters and angle functions of the zenith distance ( z  = 90 ° minus the angle of elevation). For zenith distances z  <70 ° one can write approximately for the refraction r at sea level with average air pressure :

Stars appear raised

The astronomical refraction bends every ray of light downwards - for an observer on earth all stars appear higher than would be the case without the earthly atmosphere. Its amount depends mainly on the tangent of the zenith distance and on the temperature and air pressure at the observer's location. At a height of 5 km it sinks to about 50% of its value from sea level.

The cause of the astronomical refraction is the refraction to the perpendicular , which every ray of light experiences when passing from an optically thinner medium into a denser one. It occurs in differentially small steps between adjacent layers of air on ( Snell's Law ) and will have over the entire optical path integrated be.

For this purpose, a suitable approach of the temperature and pressure curve according to the altitude is necessary - a so-called norm or standard atmosphere (near the ground: 15 ° C temperature and 1013.25  hPa air pressure, vertical temperature gradient −6 to 7 K / km). It can be approximated by assuming the atmosphere as an 8 km thick plane-parallel plate of air ("height of the homogeneous atmosphere").

In fact, the astronomical refraction deviates from this standard value if the air layers are not regularly stored. If they are slightly inclined - which is the case above every mountain range because of the sun and shadow side - the so-called zenith refraction occurs at the zenith instead of the value 0 .

Such refraction anomalies can reach 0.2 ″ and more and are the reason why sophisticated measurement methods are required in astronomy and geodesy if a measurement accuracy of better than 1 ″ is desired. They are also a major reason why astrometry satellites like Hipparcos can increase the accuracy of astrometry from 0.01 ″ to 0.1 ″ to 0.001 ″.

Small changes in temperature within the optical system of the telescope , dome of the observatory or camera or sensor or through cooling down during the night also cause small anomalies . In order to keep it below the measurement accuracy, the instruments must be adjusted to the ambient temperature before use or the hall refraction of the dome or the telescope opening must be modeled. This can be done better if the radiation is reduced, for example by painting the dome white or by regulating the temperature inside the telescope or satellite.

Terrestrial and satellite refraction

Satellite refraction: The angle r between apparent and true direction is significantly smaller than in the case of stars (see above).

If a ray of light runs entirely within the atmosphere, one speaks of “ terrestrial refraction ”. It occurs with every geodetic measurement on the earth's surface and counteracts the earth's curvature by about one seventh. This factor is called the refraction coefficient (common symbol k ) and was precisely determined by Carl Friedrich Gauß as early as 1800 . In the Hanover state survey , Gauss received an average of 13% of the earth's curvature ( k = 0.13).

The terrestrial refraction can be modeled or calculated in a similar way as the astronomical refraction, but local temperature changes in the air play a greater role. If the air temperature does not decrease upwards as in the normal atmosphere with 0.6 ° C per 100 meters, a beam of light curves more or less than normal. The mirror effect over hot asphalt is known when you look at it from a flat angle - for example on the motorway . Here the refraction coefficient of the air layers close to the ground is even negative (refraction coefficient down to −2.0). If the measuring beams run at a greater height above the terrain , k can still vary between 0.10 and 0.15. These anomalies (deviations of the air layers from the spherical shape ) limit the accuracy with which the height of survey points can be determined to a few millimeters to centimeters.

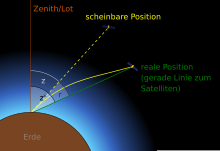
When measuring to satellites, on the other hand, the light beam does not begin or end in a complete vacuum , and the target is not “infinitely” as far away as a star. This results in a parallactic effect that can make up a few percent of the astronomical refraction (small angle s in the picture above), but also more for satellites in very deep orbits (English Low Earth Orbit , LEO).

Differential refraction

Differential refraction is the refraction of light of different wavelengths of different strengths. It is clearly noticeable at elevation angles below about 20 °. Blue light is refracted more strongly than red, so that the upper edge of observed celestial objects is lined with blue, while the lower edge is red.

This makes it difficult to observe low-lying planets , especially if they have a noticeable amount of red or blue light. For example, this is the case with Mars in its favorable opposition in summer 2018 and also with Jupiter .

For amateur telescopes , differential filters have been available for a short time, which reduce this effect somewhat.

Effect on distance measurements

Sometimes the term refraction is also used for the atmospheric effects in distance measurement, where it is not the change of the angle but the wavelength that is decisive. Here, too, relatively complex formulas are necessary for a precise reduction of measured values, of which that of the Finnish geodesist Juhani Saastamoinen (1972) for changing an EDM measuring section through the atmosphere is the best known:

Here z is the zenith distance, the geographical latitude , H the mean height of the points , p the mean air pressure, T the integral air temperature (in Kelvin) and e the vapor pressure as well as the other parameters B and δ .

Random refraction effects in the atmosphere

Effect of strong air turbulence on the perception of the lunar surface ( Clavius crater , 220 km)

Turbulence in the earth's atmosphere enlarges and reduces the image of a star so that it appears brighter and paler several times a second. This blinking perceived by the eye is called scintillation .

Image blurring and movement also occur. All three effects are summarized under the term seeing .

In addition, there is the influence of the hall refraction - a slight deflection of light at the gap in the observatory dome if there is still a small difference between the inside and outside temperature .

See also

literature

Web links

Individual evidence

  1. ↑ a b Christian Hirt: Monitoring and analysis of anomalous refraction using a digital zenith camera system . In: Astronomy and Astrophysics . 459, No. 1, 2006, pp. 283-290. doi : 10.1051 / 0004-6361: 20065485 .
  2. ↑ J. Saastamoinen: Contributions to the theory of atmospheric refraction . In: Bulletin Géodésique . tape 105 , no. 1 , 1972, p. 279-298 , doi : 10.1007 / BF02521844 .