Vapor pressure

Vapor pressure curves of some liquefied / liquefied gases

The vapor pressure is the pressure that is established when a vapor with the associated liquid phase is in thermodynamic equilibrium in a closed system . The vapor pressure increases with rising temperature and depends on the substance or mixture present. If the vapor pressure of a liquid in an open system is equal to the ambient pressure, the liquid begins to boil .

Explanation

In a liquid, the particles tend to leave the liquid association at a temperature greater than zero Kelvin. This is counteracted by surface tension and the external pressure acting on the liquid. The surface tension decreases with increasing temperature, whereby the vapor pressure increases. At the boiling point the surface tension is zero and the vapor pressure is equal to the external pressure.

Definitions

The graphic shows schematically how particles change from the liquid phase to the gaseous phase and vice versa due to their vapor pressure. The proportion of particles that go into the gas phase is usually greater because they can be distributed in space.

Substances can occur in the three classic physical states solid, liquid and gaseous. If a substance exists in parallel in gaseous and liquid phase , the gas phase is called vapor . So the vapor pressure is the pressure in a multiphase system.

In a closed system, an equilibrium is established between the liquid and the gaseous phase. The partial pressure of a component is then referred to as the vapor pressure. To emphasize that the equilibrium has been fully established, the term saturation vapor pressure is also used.

If there is no liquid phase, but only a gaseous phase, it is not a question of a vapor pressure, but a partial pressure - in the case of only one component in the gas phase, this is equal to the gas pressure .

If there are different substances in the system under consideration, the measured pressure of the gas phase is made up of the partial pressures of the different substances. The condition is that these behave like ideal gases ( Dalton's law ).

Definition in terms of physics

In physics and chemistry, vapor pressure denotes the partial pressure of a gas (multi-component system) that is in thermodynamic equilibrium with its liquid or solid phase ; it can be calculated using Raoult's law . In the one-component system, this pressure is called the equilibrium pressure.

Definition in terms of meteorology

In meteorology , vapor pressure is understood to be the partial pressure of the gas (here usually the water vapor pressure ). The maximum vapor pressure that prevails at saturation is identified as the saturation vapor pressure, identical to the definition of vapor pressure in chemistry .

Water vapor pressure

Density of liquid water (blue) and water vapor (red) as a function of the temperature at the prevailing vapor pressure. When heated to 0-4 ° C, water initially increases its density anomalously from about 0.9998 to 1,000 kg / dm ³ and then gradually decreases due to thermal expansion to about 0.310 kg / dm ³ , although the pressure acting on the liquid increases progressively . The vapor pressure above water, the saturation vapor pressure at 0 ° C is roughly 0.006 bar = 6.11 hPa, reaches 10 Torr at 10 ° C (rule of thumb for water jet pumps on cold water from 5–25 ° C) = 1/76 bar = 12, 28 hPa, increases up to 100 ° C to 1.013 bar = 1013 hPa = 0.1013 MPa and at 374 ° C to 22.1 MPa = 221 bar. With this pressure increase to around 3.6 million times, the density of the vapor phase also rises to 0.310 kg / dm ³ . - Here at the critical point there are no longer any different phases. - Values in Pa are taken from a vapor pressure table.

Vapor pressure of water: If water and water vapor are heated in a closed container, the pressure rises sharply with the temperature, and the properties of liquid and vapor become more and more similar, up to the critical point at T _c = 373.946 ° C and p _c = 22.064 MPa liquid and vapor can no longer be distinguished.

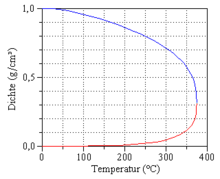
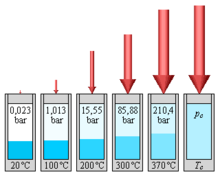
If water and water vapor coexist in thermodynamic equilibrium, the pressure is a pure function of the temperature:

{\ displaystyle p = p _ {\ mathrm {s}} (T)}

This temperature-dependent and substance-specific pressure is called the vapor pressure and the graph of this function is called the vapor pressure curve. The vapor pressure curve ends at the critical point.

As the temperature rises, the vapor pressure and vapor density rise sharply, while the density of the liquid decreases. The properties of water and steam become more and more similar with increasing temperature, until at the critical point at T = T _c = 373.946 ° C and p = p _c = 22.064 MPa the difference has completely disappeared and only a single phase still exists. When the critical point is approached, the heat of evaporation disappears, and strong density fluctuations occur, recognizable as critical opalescence .

Practical meaning

In an open pot, heated water boils when its vapor pressure exceeds the ambient air pressure. The boiling temperature of the water is therefore dependent on the air pressure and decreases with increasing altitude, since the natural air pressure of the earth decreases with increasing distance from sea level. At an altitude of 2000 m, water boils at 93 ° C, at an altitude of 8000 m it boils at 74 ° C.

The physical laws governing vapor pressure and evaporation (vapor pressure curve, Clausius-Clapeyron equation, etc.) were first investigated and formulated in connection with the steam engine . Here, too, there is a coexistence of liquid and gas. The steam engine made use of the fact that the steam pressure is independent of the volume as long as one moves in the two-phase system "liquid-gas". The only thing that changes at constant temperature is the “liquid-gas” ratio. The pressure in the tank, which moves the piston, does not change as a result of the piston movement (piston movement, volume change in the cylinder). However, the piston position must not be changed so far that one of the phases would disappear. ${\ displaystyle \ rightarrow}$

calculation

The saturation vapor pressure can be calculated , for example, using the Lee-Kesler and Ambrose-Walton methods . Both methods are based on the correspondence principle , in which critical data and the acentric factor are used.

The vapor pressure equations , which use substance-specific parameters adapted to experimental data, such as the Wagner and Antoine equations, meet higher accuracy requirements .

Water vapor pressure in meteorology

In meteorology, the term vapor pressure is usually understood to mean the vapor pressure of the water vapor (water vapor pressure) and thus its partial pressure. The vapor density corresponds to the absolute humidity .

The vapor pressure according to the definition of meteorology, i.e. the partial pressure of a gas within a gas mixture, can be approximately calculated by converting the general gas equation with the following formula:

{\ displaystyle e = \ rho _ {i} \ cdot R_ {i} \ cdot T.}

The individual symbols stand for the following quantities :

e - vapor pressure,
ρ _i - vapor density (absolute humidity),
R _i - individual gas constant (for water vapor: 461.5 J / (kg K)),
T - absolute temperature .

At an air temperature of 20 ° C ( T = 293.15 K) and maximum humidity at this temperature and normal pressure ( ρ _i = 0.017 kg / m³), the vapor pressure calculated in this way is about 23.39 hPa.

Since the water vapor partial pressure makes up only a small part of the air pressure , a thermodynamic equilibrium only arises after a very long period of time, which means that substantial undersaturation in the earth's atmosphere is possible without the existing liquid water boiling immediately. For this reason and the high dynamics in the atmosphere, thermodynamically stable states are usually rarely or only briefly encountered, especially in very weather-active zones of the earth's atmosphere. Due to the locally relatively higher vapor pressure above the liquid phase (see above), when water and ice are simultaneously present in a cloud, the ice particles grow at the expense of the water droplets.

The vapor pressure is lower over a non-superheated solid phase than over a liquid phase of the same temperature. If both phases are in contact with one another via the gases surrounding them, the proportion of solid matter increases at the expense of the liquid . This is due to the fact that the stronger binding of the particles in the solid and the resulting heat of fusion in the case of sublimation , i.e. the solid-gaseous phase transition , must also be overcome or applied. The consequence of this is that evaporation or evaporation of particles in the liquid phase occurs more easily and thus more frequently than sublimation of particles above the solid phase. So there are more particles in the gaseous state above the liquid than above the solid, which increases the vapor pressure locally and leads to the growth of the solid phase.

literature

Vapor pressure value tables for various substances:

K. Scheffler, J. Straub and U. Grigull: Wasserdampftafeln. Thermodynamic properties of water and water vapor up to 800 ° C and 800 bar. Springer-Verlag, Berlin 1981, ISBN 3-540-10930-7 .
U. Grigull, J. Straub and P. Schiebener: Steam Tables in SI Units. Steam panels. Springer-Verlag, Berlin 1990, ISBN 3-540-51888-6 .
BI Lee, MG Kesler: A generalized thermodynamic correlation based on three-parameter corresponding states . AIChE J, 21, 1975, p. 510, doi: 10.1002 / aic.690210313 .
KS Pitzer, DZ Lippmann, RF Curl, Jr., CM Huggins, DE Petersen: The Volumetric and Thermodynamic Properties of Fluids. II. Compressibility Factor, Vapor Pressure and Entropy of Vaporization . J. Am. Chem. Soc. 77, 1955, p. 3433, doi: 10.1021 / ja01618a002 .
W. Wagner, J. Ewers, W. Pentermann: New vapor-pressure measurements and a new rational vapor-pressure equation for oxygen . J. Chem. Thermodyn. 8. 1976, p. 1049, doi: 10.1016 / 0021-9614 (76) 90136-1 .
D. Ambrose, J. Walton: Vapor pressures up to their critical temperatures of normal alkanes and 1-alkanols . Pure Appl. Chem. 61, 1989, p. 1395, doi: 10.1351 / pac198961081395 .

Web links

Wikibooks: Collection of tables chemistry / material data water - learning and teaching materials

IAPWS (International Association for the Properties of Water and Steam)
Calculation of thermodynamic quantities with NIST Chemistry Webbook (English) http://webbook.nist.gov/chemistry/fluid/
Video: vapor pressure, an example of phase equilibrium . Jakob Günter Lauth (SciFox) 2019, made available by the Technical Information Library (TIB), doi : 10.5446 / 40353 .

Individual evidence

^ Karl Stephan, Franz Mayinger: Thermodynamics - Volume 1: One-material systems. Basics and technical applications , Springer Berlin Heidelberg 1998, appendix: Steam tables - Table I. State variables of water and steam at saturation (temperature table) , doi: 10.1007 / 978-3-662-13213-5 .

[1] Karl Stephan, Franz Mayinger: Thermodynamics - Volume 1: One-material systems. Basics and technical applications , Springer Berlin Heidelberg 1998, appendix: Steam tables - Table I. State variables of water and steam at saturation (temperature table) , doi: 10.1007 / 978-3-662-13213-5 .