Phase transition
A phase transition or a phase transformation or phase transformation is in thermodynamics the transformation of one or more phases of a substance into other phases. Phase diagrams provide a graphical representation of the stability ranges of the phases depending on the state variables such as pressure , temperature , chemical composition and magnetic field strength . In these diagrams, the stability areas are limited by phase boundary lines on which the phase transitions occur.
classification
Phase transitions can u. a. occur between solid, liquid and gaseous phases. There are special terms for phase transitions between certain states of aggregation (so-called changes of states of aggregation ):
- Melting (transition from solid to liquid)
- Evaporation (transition from liquid to gas)
- Sublimation (transition from solid to gaseous)
- Solidification , also freezing or crystallizing (transition from liquid to solid)
- Condensation (transition from gaseous to liquid)
- Resublimation (transition from gaseous to solid)
In some material systems , the phase interfaces between the liquid and gaseous phase disappear above a critical point , which is characterized by a critical temperature and a critical pressure . Under these conditions, liquid and gas are only one phase that is called "supercritical". This means that there can no longer be any evaporation or condensation.
Likewise, in some material systems there can be a triple point at which both a solid and a liquid and a gaseous phase are in equilibrium with each other and, accordingly, all six first-mentioned forms of the phase transition take place simultaneously.
Other types of phase transitions are mentioned below.
Classification according to Ehrenfest
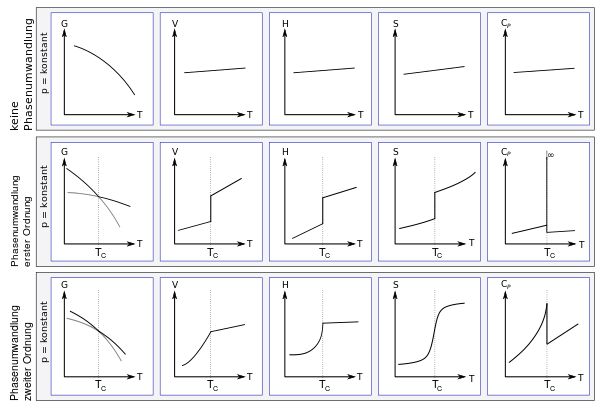
Basically, phase transitions according to the Ehrenfest classification (according to Paul Ehrenfest ) are divided into different orders. To do this, one considers thermodynamic quantities such as volume , enthalpy or entropy as a function of one (or more) variables, usually temperature. The system is described by a thermodynamic potential G ( Gibbs energy , free enthalpy). In the case of a phase transition of the nth order, G as a function z. B. Considered the temperature (or the pressure) together with its first n-1 derivatives continuously , only the n-th derivative is discontinuous.
Phase transitions are described in more detail in Landau's theory , where the phases change from disordered phases to ordered phases with the simultaneous appearance of a new order parameter as a result of symmetry breaks. These are characterized by accompanying jumps of macroscopic quantities such as magnetization or the deformation of a crystal lattice .
The distinction between first-order and higher-order phase transitions ( continuous phase transitions ), especially second-order, is of particular importance . In fact, in the modern classification only this distinction is made:
- An example of a first-order phase transition is the transition of a liquid such as water to a solid at the freezing point . In order to convert from the solid to the liquid state, additional thermal energy (in the form of latent heat ) must be added without an actual temperature increase occurring. Since this results in a discontinuity in the entropy (the first derivative of the free enthalpy G according to temperature), the melting of ice is a first-order phase transition. Likewise, the volume (first derivative of G with respect to the pressure p) makes a jump at the phase boundary ; The resulting difference in density between the phases corresponds to the order parameter in land theory. A jump in the order parameter is typical for phase transitions of the first kind.
- An example of a second-order phase transition or a continuous phase transition is the transition from the ferromagnetic to the paramagnetic phase at the Curie temperature in a ferromagnet. The order parameter is the magnetization, which steadily tends towards zero at the phase transition without any additional latent heat occurring. However, there is a jump in the second derivative of the free enthalpy after the temperature ( heat capacity ). This behavior marks a second order phase transition. A continuous transition in the order parameter is typical here. Another example of a second order phase transition is the transition from normal metal to superconductor .
The following figure shows the first and second order phase transitions according to Ehrenfest. At constant pressure, the figure shows the free enthalpy G, the volume V, the enthalpy H, the entropy S and the heat capacity C P , each depending on the temperature. In the top row, the parameters are shown without a phase transition, in the middle a phase transition of the first order and in the bottom row a phase transition of the second order. The phase transformation takes each at the critical temperature T C instead. In the figure, the curves of the free enthalpy of the respective phase are drawn and continued in gray in the respective other phase; there they can predict hypothermic effects or metastability .
Further classifications
In addition to this basic classification, there are a number of other distinctions in special areas of application.
Structural classification
According to the structural classification, a distinction is made in mineralogy :
- discontinuous phase transitions, characterized by the breakage of chemical bonds . One example is the transformation of graphite into diamond .
- martensitic phase transitions in which the crystal lattice is sheared . One example is the conversion of γ- to α-iron.
Martensitic phase transitions are broken down again into:- athermal phase transitions (degree of conversion not time-dependent)
- isothermal phase transitions (degree of conversion depends on time).
- Continuous phase transitions are only associated with one order of the crystal structure .
There are two subtypes:- Displaced phase transitions in which there is a shift or rotation of the atomic positions (e.g. when converting high quartz into deep quartz ).
- Order-disorder phase transitions in which there is an order of several atoms statistically distributed over different atomic positions, so that each position is occupied by only one type of atom.
- In both cases, large-scale periodicities can occur which superimpose the lattice structure. These are called incommensurable structures.
Kinetic classification
The kinetic classification divides phase transitions according to their reaction rate into:
- Zero order phase transitions in which the reaction rate is constant
- First-order phase transitions, in which the reaction rate depends on the concentration of an initial phase
- Second order phase transitions, in which the reaction rate depends on the concentrations of two starting substances, etc.
Fluid dynamics classification
In terms of flow dynamics , a distinction is made between speed transitions, where flow properties change suddenly and massively, e.g. B. the change in important values such as drag and buoyancy in gases and liquids. An important area is the critical transition from subcritical to supercritical (see Reynolds number , laminar flow , turbulent flow ).
Examples
Phase transitions are often associated with changing certain material properties, for example:
- Change of the crystal structure ( structural phase transition ) or the adsorbate structure .
- Change between ferromagnetic and paramagnetic behavior at the critical or Curie temperature
- Change between different magnetic orders, e.g. B. from commensurable to incommensurable magnetic structure
- Change between ferro- and dielectric behavior
- in high-energy physics: formation of quark-gluon plasma at high temperatures and pressures
- Transition to super fluidity
- Transition to superconductivity
- Transition from subcritical flow to supercritical ( flow dynamics ).
- Transition from a smooth to an atomically roughened crystal surface ( faceting )
theory
The theory of continuous phase transitions is based on an order parameter (e.g. the magnetization when converting a ferromagnet into a paramagnet). In the case of continuous phase transitions, the order parameter tends towards zero as the point of transition is approached (on the other hand, it jumps at a phase transition of the first order), and the correlation length diverges (in the case of a conversion of the first order it remains finite).
Very different types of continuous phase transitions can be summarized in universality classes, which is ultimately again due to the divergence of the correlation length. These classes can be characterized by a few parameters, for example by a critical exponent . This is the exponent of a power law that describes how an order parameter disappears near the critical point, e.g. B. as a function of the distance between the temperature and the critical point.
The relationship between the fundamental symmetries of the respective phases and the values of these parameters has been extensively investigated theoretically in the framework of statistical physics over the past decades and has also been checked in a large number of experiments and computer simulations .
The Landau or mean field theory is sometimes used in theoretical descriptions of phase transitions . Here, however, critical thermal fluctuations are neglected, which can play an essential role in the vicinity of the transition (and are observed, for example, in the critical opalescence ). The Landau theory can nevertheless provide valuable initial insights as a starting point for more precise theories (from the scale theory of Pokrowski and Patashinski to the epsilon development by KG Wilson and ME Fisher ).
This has been recognized in particular by Kenneth G. Wilson, who received the Nobel Prize in 1982 for pioneering work on continuous phase transitions. Wilson is one of the decisive pioneers of renormalization group theory , which takes into account that with continuous phase transitions the critical fluctuations take place in self-similar form on many length scales . Analog theories are used today in many areas of physics and mathematics.
Significance for mineralogy
Knowledge of the physicochemical conditions under which phase transitions occur allows mineralogists to draw conclusions about the history of rock formation. When a rock is exposed to high pressures and temperatures, a phase change occurs in many cases. Assuming that the subsequent cooling takes place so quickly that the reverse reaction no longer takes place due to the diffusion that is hardly possible at low temperatures, one can assume that the minerals that are stable at high temperatures and pressures will be "frozen" and so on Earth's surface are preserved. This enables statements to be made about the temperatures and pressures a rock has "seen" in the course of its genesis. Examples of this are the phase transitions between andalusite , sillimanite and thistene in the area of aluminosilicates, the conversion of graphite into diamond and of quartz into coesite or stishovite . The knowledge of phase transitions acquired through experimental mineralogy also explains the rheological behavior of the earth's mantle: The iron-magnesium silicate olivine is transformed at a depth of 410 km into the wadsleyite , which crystallizes in the β-spinel structure , which in turn is further in the converts ringwoodite occurring in the γ-spinel structure (see also the articles 410 km discontinuity and 520 km discontinuity ). There are no chemical changes at all, only a change in the crystal structure. Using the example of the conversion of coesite into stishovite, it is easy to explain why a phase transition occurs: Under normal conditions, silicon is surrounded by four oxygen atoms , but under high pressures the atoms move closer together so that the coordination by six oxygen atoms is energetically more favorable .
Significance for technical processes
During ceramic firing is converted at a temperature of 573 ° C silica in high quartz order. The volume changes in the process. If the heating rate is too high, this can lead to the ceramic cracking. The heating rate is therefore throttled in this temperature range.
In the field of conservation of art objects, the objects are often stored in a cool and dry place and are also exhibited. This is not correct for objects made of tin , because below 15 ° C this changes into another modification, the external appearance of which is not very attractive and which is known as tin plague .
For art history it is interesting to know that in the past the blue pigment azurite was often used to depict the sky. Over the centuries, however, this has been converted into the thermodynamically stable form malachite , which is green. As a result, the sky is sometimes green in old pictures.
In steel production, the transformation of the iron modification from austenite to ferrite or martensite is associated with changes in the structure, which are of great importance for the properties of the steel.
In two-dimensional materials, e.g. B. in thin magnetic layers, there can only be long-range order and thus a phase transition under limited conditions. This interesting aspect is dealt with in the Mermin-Wagner theorem (after N. David Mermin and Herbert Wagner ) and has also been investigated experimentally.
Paraffins have a particularly large change in volume of around 30% during the phase transition from solid to liquid. This hub can be used for the construction of actuators .
Measurement methods
A number of methods are used to measure phase transitions, such as: B .:
- Thermogravimetry (most common method)
- X-ray diffraction , neutron diffraction (e.g. high and low temperature powder diffractometry )
- Raman Spectroscopy
- UV / VIS spectroscopy
- SQUID (measurement of magnetic transitions)
- Hall effect (measurement of magnetic transitions)
- Mössbauer spectroscopy (simultaneous measurement of magnetic and non-magnetic transitions. Up to max. Approx. 800–1000 ° C)
- Disturbed gamma-gamma angle correlation (simultaneous measurement of magnetic and non-magnetic transitions. Unlimited temperature range, tested up to over 2000 ° C, theoretically up to the highest melting solid tantalum hafnium carbide at 4215 ° C.)
See also
- Chaos theory
- Geothermobarometry
- Complex system
- Quantum phase transition
- Delayed boiling
- Tipping point
- Hypothermia (thermodynamics)
- Oversaturation
- Van der Waals equation
literature
- HE Stanley : Introduction to Phase Transitions and Critical Phenomena . Oxford University Press, 1971.
- W. Gebhard, U. Krey: Phase transitions and critical phenomena . Vieweg, 1980.
- C. Domb, MS Green, JL Lebowitz (Eds.): Phase Transitions and Critical Phenomena . tape 1-20 (1972-2001) . Academic Press.
- ME Fisher : Renormalization Group in Theory of Critical Behavior . In: Reviews of Modern Physics . tape 46 , 1974, pp. 597-616 .
- Mats Hillert: Phase equilibria, phase diagrams and phase transformations - their thermodynamic basis . Cambridge University Press, Cambridge 2008, ISBN 0-521-85351-6 .
- Pierre Papon et al. a .: The physics of phase transitions - concepts and applications . Springer, Berlin 2006, ISBN 3-540-33389-4 .
- Vadim V. Brazhkin: New kinds of phase transitions - transformations in disordered substances . Kluwer Academic, Dordrecht 2002, ISBN 1-4020-0825-2 .
Web links
Individual evidence
- ↑ Hans-Dieter Jakubke, Ruth Karcher (coordinators): Encyclopedia of chemistry in three volumes, Spektrum Verlag, Heidelberg, Volume 3, 1999, ISBN 3-8274-0381-2 , pp 11-12.
- ↑ W. Dieterich: Theory of phase transitions. (PDF) Script, University of Konstanz, p. 5.
- ↑ Govindhan Dhanaraj, Kullaiah Byrappa, Vishwanath Prasad, Michael Dudley (Eds.): Springer Handbook of Crystal Growth . [Electronic Resource]. Springer, Heidelberg 2010, ISBN 978-3-540-74761-1 , p. 191 ( limited preview in Google Book search).