Dynamic lift
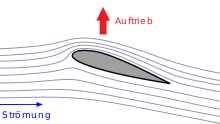
In fluid mechanics, dynamic lift is the portion of the force acting on a body in a flow that is perpendicular to the direction of flow. Dynamic lift is the basic physical principle for the natural flight of birds and bats . He is also the basis for the function of the wings of aircraft , the propeller , the propeller , the sailing , the turbines and buoyancy Runner -Windkraftanlagen. Effects of dynamic buoyancy are also used to control submarines and airships .
The creation of buoyancy by the flow is explained with the method of fluid dynamics . This is part of classical mechanics and obeys Newton's laws and the laws of conservation derived from them (conservation of momentum , angular momentum and energy ). With a compressible medium ( gas ), a thermodynamic consideration of the processes is also necessary.
Buoyancy arises when the air flows around appropriately shaped bodies, e.g. B. wings by accelerating air downwards . The downward force on the air is the counterforce of the upward force on the wing, the lift. Buoyancy forces can also act towards the ground and are then referred to as downforce. In racing vehicles, contact pressure can be generated with the help of front and rear wings .
introduction
When a body of a certain shape and orientation moves relative to a gas or liquid, forces that are caused by the flow around it act on the body. In contrast to static lift , the direction of dynamic lift is not defined by gravity , but by the direction of the flow. The resulting flow force acts on the pressure point and can be broken down into two components, the resistance in the direction of flow and the lift perpendicular to it.
- The dynamic lift is the part of the resulting air force that acts perpendicular to the flow:
- The part of the resulting air force that acts parallel to the flow is the flow resistance .
- Mean:
- the lift coefficient ,
- the drag coefficient ,
- the density of the medium,
- the flow velocity of the medium,
- the reference area (in the case of lift or aerofoils, the wing area, not the cross-sectional area in the direction of flow).
The coefficients of lift and drag depend on the shape and orientation of the body in the flow. In the case of wings , the shape and orientation are referred to as profile and angle of attack . The angle of attack is the angle between the chord of the wing and the direction of flow of the medium. The dynamic lift on a wing (with its given profile) is determined by the angle of attack of the wing and its area as well as the density of the medium and its flow velocity .
Working principle
The properties of air , its mass and its low viscosity (toughness) are important for understanding dynamic lift. In the subsonic range up to about 0.3 Mach , air is an incompressible fluid , and the laminar flow around the wings can simulate potential flows to a good approximation. With these prerequisites, the basic principle of dynamic lift can be described in a qualitatively more understandable manner than at higher speeds.
Applying Newton's laws, the following applies in particular: When an amount of air (i.e. a certain mass) is accelerated, a force acts and the air mass increases its speed. This means that an impulse (product of mass and speed) is transferred to the amount of air.
Wings generate momentum


For basic considerations to understand the statement “lift on wings is created by the deflection of the air downwards”, the air space is composed of cubic, air-filled space elements. Each of these air volumes must be carried by its surroundings against gravity, otherwise it would fall to the ground:
- Volumes that only contain air are carried by the environment by the static buoyancy according to Archimedes . The pressure difference between the lower surface and the upper surface of a volume, which results from the pressure decrease with increasing height , is the counterforce to gravity (see also hydrostatic pressure ).
- Volumes that completely contain the aircraft (the bird ...) must be carried by their surroundings together with the aircraft.
- For this purpose, air is constantly accelerated from the wing in the vertical direction downwards ( downwash ) within the volume . This means that an impulse is transmitted downwards to the air . According to Newton's second law , this downward acceleration of the air flow requires a force. According to Newton's third law ( actio and reactio ) an equal and opposite force, the lift, acts on the wing.
This force generated by accelerated air is not difficult to observe:
- The table fan exerts a noticeable force when you hold it in your hand or direct its airflow towards you.
- In the vicinity of a low-hovering helicopter ( rotary wing aircraft ) you can clearly feel the downdraft generated by the rotors , see also Fig. 5.
- Airplanes that fly over a smooth cloud cover at close range leave a clear track in the cloud cover, see Fig. 6.
The acceleration of the air is achieved in two ways with a wing as in Fig. 4 :
- Downward pressure force through overpressure on the underside of the wing, and
- Pulling force upwards through a negative pressure on the upper side of the wing.
The compressive force is created by accelerating the air downwards on the underside of the wing as in Fig. 4 . According to Newton's second law “force equals mass times acceleration”, this can only be achieved with a downward force, which is counteracted by the lift according to actio and reaction, i.e. upward. The pressure under the wing is also increased by the ground effect , see there.
The upward pulling force arises from the faster flow on the upper side of the wing compared to the slower flow on the underside, see Fig. 11 . According to the Bernoulli equation , which applies to potential flows between any two points, the pressure on the upper side is therefore lower than on the lower side, which means that air above the profile is accelerated downwards, generating a buoyant force. The faster flow on the upper side of the wing is caused by the #circulation and the # Venturi effect , commonly known as the nozzle effect.
The body experiences buoyancy only through corresponding force effects, which are applied in fluid dynamics via surface-distributed forces. These result from the flow around which is determined by the speed and pressure distribution. Both influence one another and cannot be viewed separately from one another. Attempts at an explanation based on only one effect are therefore incomplete. Explaining the lift only from the positive angle of attack fails because of the lift of a rotating ball without an angle of attack, see #Circulation . Ludwig Prandtl was able to build up a whole wing theory for large Reynolds numbers on the circulation . The circulation explains the pressure differences on the surface, but not how the weight of the aircraft is carried by the fluid. It is difficult to explain the pressure differences above and below the wing solely with the Venturi effect, given the different effects on and under the wing, see Fig. 12 . The often quoted Bernoulli equation ultimately only makes a comparison between points in the flow field; it does not explain what causes differences that arise.
The generation of impulses is therefore a consequence
- the angle of attack of a body surface against the flow,
- the circulation around the body and
- the Venturi effect,
whose contribution to dynamic lift is the subject of the next sections.
Angle of attack

The first of the mentioned possibilities to generate lift through a positive angle of attack is based on the same principle as the two-dimensional impact . If a fluid mass collides with a positively inclined surface as in Fig. 4 from below, it gets a velocity component in a vertical direction downwards. The "impact force" ( inertia force ) exerted on the surface has two components:
- The proportion in the direction of flow acts in this direction on the profile, which is noticeable in an increased flow resistance and the C w value increases.
- The vertical component accelerates the surface minus the acceleration due to gravity in the vertical direction, which contributes to the fact that the surface rises, remains at the same height or falls, depending on which of the acceleration components predominates.
The effect is supported by easily comprehensible experiments and observations:
- A hand held out of a fast moving car experiences an upward or downward force on the side facing the flow, depending on the angle of attack.
- A postcard, moved horizontally and at a positive angle over a candle, makes the flame flicker even from a surprisingly high height. If you move the card correspondingly quickly, the flow resistance becomes noticeable and the card bends.
Through interaction with the surrounding medium and the negative pressure on the upper side of the profile, as in Fig. 12 and 13 , not only fluid balls that hit the wing are deflected downwards, but also those below and above, see Fig. 4 , which is essential for lift, the above impact effect and the #pulse flow contributes. Therefore the angle of attack is not sufficient as the sole explanation of the lift. Von Lössl's law of shock adapts better to experience, but lacks any hydrodynamic justification.
A large angle of attack as in Fig. 4 shows a large flow resistance, see Fig. 7. In normal flight operations outside of the take-off and landing phase, the angle of attack is well below 10 ° and this type of lift generation is of little importance. If the angle of attack is greater than α C A , Max , boundary layer detachments initially occur with reverse flow areas on the wing and lift decreases; Finally, when the stall occurs , the lift is greatly reduced. The diagram also shows that the associated profile generates lift even with a negative angle of attack, which is a result of the circulation and the pressure conditions on the wing.
circulation
A spinning ball without a defined angle of attack also experiences buoyancy. This buoyancy is explained by the circulation of a flow, see Fig. 8. The superposition of a flow subject to circulation on a profile flow strengthens it on the top side of the profile and counteracts it on the bottom side. According to Bernoulli's equation, this means a decrease in pressure on the wing and an increase in pressure on the underside of the wing, i.e. H. buoyancy is formed. In the case of cylinders and spheres, buoyancy arises when they rotate and create a circulation due to the static condition , see Magnus effect .
The formation of the circulation that is necessary for lift can be seen on the aircraft in Fig. 9. When the wing starts, a starting vortex sets in at the trailing edge , which, due to the conservation of angular momentum and Kelvin's vortex law, requires a reverse circulation around the wing, a vortex called a bound vortex. It is created in viscous fluids by a separation surface with a sudden change in speed at the trailing edge of the wing, see approach vortex , which also swims in amount and direction with every change in speed. The closed fluidized system in Fig. 9 is the linking of bound vortex Anfahrwirbel and the tip vortex .
The starting vortex remains at the point of origin. Therefore, this effect only shows when the starting vortex has detached. Without this, a symmetrical profile theoretically always has a zero lift angle of 0 °.
Venturi effect

The lift- generating circulation is determined by the profile , which influences the dynamic lift. The moving wing with zero angle of attack pushes itself through the fluid, whereby it is displaced up and down, directed onto a curved path and pressed together perpendicular to the surface. Due to the Venturi effect , commonly known as a nozzle effect, the medium is accelerated parallel to the surface, cf. Fig. 10. This can be seen from the streamlines in Fig. 4 , because the volume flow between two streamlines in laminar areas is the same everywhere, see flow function . The distance between the streamlines narrows above the profile, the speed increases and the pressure according to Bernoulli decreases accordingly. As in a vortex , the pressure decreases in the direction of the center of curvature and increases in the opposite direction. At the thickest point of the non-recessed profile, the pressure on the top is minimal, see Fig. 13 . Under the profile, the effect of the angle of attack dominates in Fig. 4 and Fig. 12 and the streamlines move apart, as a result of which the speed decreases and the pressure increases.
The upper side of the wing sloping towards its trailing edge creates more space for the medium (volume increase), into which the medium flows in a laminar manner against the increasing pressure, thanks to its kinetic energy, see Fig. 12 and 13 . If the pressure rise is too great, a laminar boundary layer separation can occur, which reduces the lift, see also #Angle of attack .
Physical quantities involved in buoyancy
This section first describes the flow field around a wing . The most important forces and their contribution to buoyancy are then discussed.
Flow field
With the asymmetrical profile, acceleration in the direction of movement, i.e. backwards, is much stronger on the upper side of the profile than on the lower side. The lift- generating #circulation is shown in the speed differences . With a positive angle of attack there is a slight acceleration in the direction of the movement on the underside, like a bow wave.
The influence of the profile is strongest near the surface. This means that originally adjacent particles of the medium, which were separated from the front of the profile, do not meet again behind the profile. Rather, they remain permanently separated - in the example shown here of a simulated flow by almost a profile depth. The offset of the medium flowing above compared to the lower can be observed experimentally with pulsed smoke plumes.
pressure
In a wing with positive pitch, as shown in Fig. 12 and in accordance with the streamlines in Fig. 4 , the pressure under the wing is increased and above the wing is decreased. When the wing is not or negatively inclined, the pressure under the wing is also lower than that of the far field, see Fig. 13. The lift force results from the resultant of the pressure forces on the wing and this resultant is directed upwards in both cases.
At a great vertical distance from the wing there is positive pressure below and negative pressure above. Regardless of the pressure fluctuations in the near field, the integration of the pressure forces on (infinitely) extended horizontal surfaces results in a uniform picture: Each such surface below the wing carries half the lift force ½A whereas each surface above -½A absorbs. The lift force A is carried by two planes between which the wing is located. This is the case , for example, with wind turbines . A floor at a finite distance modifies the conditions in such a way that every surface between the floor and the missile, including the floor, absorbs the entire lift force and every surface above the body is totally free of forces.
As the distance increases, the change in air pressure through the wing decreases. This allows the definition of an area of influence as the area around the wing within which the pressure has a significant share in the total lift. This area of influence is always small (perhaps up to 100 m for commercial aircraft) in relation to the flight altitude of 10 km and more, see also #Three-dimensional flow field below.
Momentum flow
If air particles get into the wing's area of influence as defined above, they are accelerated downwards, see Fig. 4 . Vertical impulse is produced according to its mass. This impulse production is the counterforce that the aircraft carries. After leaving the area of influence, no more force acts on the air particles - their momentum is retained.
The lift force is now the product of the mass flow and the vertical speed. In terms of formulas, this results from the pulse rate :
Therein which forms over point , the time derivative of the mass m or speed . While the first term predominates in the lift force near the wing, the second term is dominant in the far field.
As the distance from the aircraft increases, the air jet mixes with the surrounding still air and is slowed down. The buoyancy remains unchanged, as the moving mass increases accordingly. When it hits the ground, the weight of the aircraft is transferred to the ground as a compressive force, which absorbs the momentum, see also #Three-dimensional flow field below.
viscosity
The viscosity of the air is important for the generation of eddies and the circulation, see #circulation . According to the (first) Helmholtz vortex law and the Kelvin vortex law , vortices cannot arise or disappear in flow areas of viscosity-free fluids; this is only possible in viscous fluids. In the case of laminar flow, the effects of viscosity only play an important role in the boundary layer of the wing and can lead to boundary layer separation with transition to a turbulent flow , see # angle of attack .
Further information
Three-dimensional flow field
The relatively higher pressure under the wings drives the fluid particles to the edges of the wings and thus to the wing tips. There the particles flow to the upper side of the wing, where they are sucked into the center of the wing by the negative pressure. This is how the tip vortices arise .
The lift-generating circulation is not constant over the span of the wing, but decreases towards the wing tips, see Fig. 14. This course can be approximated as in Fig. 9 by wing pieces on which the circulation is constant. Each of these pieces has two tip vortices, the strength of which depends on the respective circulation. Any wing shape can be reproduced with narrower wing pieces and a corresponding number of vortex lines are created on the trailing edge of the wing , which, as shown in Fig. 14, roll up to two tip vortices at the wing tips , which become larger with increasing distance.
The aircraft's lift is generated by the bound vortex, while the tip vortices take over the transport of momentum downwards.
The weight of the air and all the bodies in it is borne by the ground with a pressure distribution as sketched in Fig. 15. The additional pressure is very low: Even if the weight of a fully loaded Boeing 747 is only related to its wings, the resulting pressure of around 0.064 bar corresponds to the pressure difference at the water surface and at a depth of 65 cm.
Where does the energy for pulse generation come from?
Because of the propulsion , the propulsion systems of aircraft constantly work against the flow resistance , a work that supplies the air with kinetic energy . Part of the work, the induced air resistance , is done by the air accelerated downwards. The induced air resistance decreases with increasing wingspan.
Since the kinetic energy of the aircraft results from its mass and speed, its speed must necessarily decrease with the generation of lift while the mass of the aircraft remains the same if no drive is available.
Energy conservation
In order to preserve the energy during mixing, it should be noted that the decrease in the mean flow velocity does reduce the kinetic energy. Nevertheless, this kinetic energy is converted into thermal energy , whereby the energy is retained as a whole.
Incompressibility
For incompressible, steady flow of a viscosity-free fluid of constant density, Bernoulli's law first applies along a trajectory : The sum of the square of the speed and the quotient of pressure and density is constant. For air particles that get into the area of influence of the wing, this means:
- When the pressure decreases, the flow velocity increases.
- When the pressure increases, the flow velocity decreases.
Bernoulli's law makes no statement about cause and effect, but only gives a relation between pressure and speed at two points in the flow field. Bernoulli's law follows from the working law .
Compressibility
So far, an airspeed has been assumed that is low compared to the speed of sound, and where the flow around a wing is incompressible with sufficient accuracy. When considering the momentum balance under the influence of forces, compressibility also makes no difference. In commercial flight and large parts of military flight, however, the compressibility of the air must be taken into account, because the work against volume change is an important part of the energetics of compressible flow.
With transonic subsonic Mach numbers of M = 0.8 the flow is compressible and there is a supersonic area on the wing, which is closed by a shock wave. The assumption of a viscosity-free flow is no longer permissible. Swept wings have a more favorable ratio of lift coefficient and drag coefficient, which was already known in 1939. Profiles for these Mach numbers are thinner so that the transition to supersonic flow takes place as far downstream as possible on the profile.
In the case of profiles in a supersonic flow, inclined compression surges occur, so that the resistance can be kept low with sharp front and rear edges.
Common errors
The dynamic lift is sometimes wrongly justified.
- The faster flow on the upper side of the profile, which is important for circulation, is occasionally explained by the fact that the fluid elements on the upper side have to cover a longer distance than those on the lower side. In order for both particles to arrive at the rear edge at the same time, the particle must flow faster on the upper side than on the lower side. However, there is no physical reason why the particles must arrive at the trailing edge at the same time; they also do not, as can be seen from Fig. 11 .
- Occasionally, the Coandă effect is used to explain why the flow follows a curved contour, especially the wing profile. The more common and simpler reason for this is simply the lack of the condition for boundary layer separation .
Web links
- D. Anderson, S. Eberhardt: A Physical Description of Flight; Revisited. (PDF; 483 kB) www.udocz.com, 2009, accessed on March 8, 2018 (English). (Excerpt from the book Understanding Flight as a PDF file)
- Holger Babinsky: Flow over aerofoils. University of Cambridge, Department of Engineering, 2003, accessed April 7, 2018 .
- NASA 's Beginner's Guide to Aerodynamics . Here is u. a. a computer wind tunnel in which one can change the main parameters of a profile and observe the effects on the flow field and forces.
- Klaus Weltner: Misinterpretations of Bernoulli's Law. (PDF; 674 kB) University of Frankfurt, January 6, 2011, accessed on June 29, 2016 (English).
- Klaus Weltner: Physics of Flight - reviewed. (PDF; 576 kB) University of Frankfurt, January 6, 2011, accessed on June 29, 2016 (English).
- Irrotational plane flows of an inviscid fluid, University of Genoa, Faculty of Engineering
Individual evidence
- ↑ a b c d Babinsky (2003): Flow over aerofoils , YouTube: "Flow over aerofoils"
- ↑ Weltner (2016): Flugphysik , p. 17
- ↑ Oertel (2012), p. 92 f.
- ^ NASA, Glenn Research Center: "Lift occurs when a moving flow of gas is turned by a solid object. The flow is turned in one direction, and the lift is generated in the opposite direction, according to Newton's Third Law of action and reaction . "
- ^ Babinsky (2003): How do wings work? , P. 502
- ↑ A Physical Description of Flight , p. 6 ff
- ↑ a b A Physical Description of Flight , p. 4
- ↑ Rita Wodzinski (1999), chap. 3: “If there is a steady flow, the force on a body in the flow can be determined by placing any control volume around the body and evaluating the incoming and outgoing momentum and the pressure at the interfaces of the control volume. No matter how you set the control volume, the buoyancy always comes out "
- ↑ Anderson, Eberhardt: Unterstanding Flight, 2nd edition , p. 4
- ^ A Physical Description of Flight , p. 7
- ↑ Picture of a Pilatus PC-24 by Paul Bowen on www.boldmethod.com
- ↑ Oertel (2012), p. 207.
- ↑ Richard Grammel : The hydrodynamic fundamentals of flight . Springer Fachmedien, Wiesbaden 1917, ISBN 978-3-663-19899-4 , p. 2 , doi : 10.1007 / 978-3-663-20240-0 ( springer.com [accessed May 8, 2020]).
- ↑ Oertel (2012), pp. 86ff, 207ff.
- ↑ Starting vortex . In: Lexicon of Physics . Spectrum Academic Publishing House, Heidelberg 1998 ( Spektrum.de ). , Oertel (2012), pp. 87, 209, Spurk (2010), p. 126.
- ↑ Oertel (2012), p. 207, Spurk (2010), p. 124.
- ↑ Spurk (2010), p. 127.
- ↑ Spurk (2010), p. 124.
- ↑ Oertel (2012), p. 207.
- ↑ Ludwig Prandtl, Albert Betz: Four treatises on hydrodynamics and aerodynamics . Universitätsverlag Göttingen, Göttingen 1927, DNB 101007458X , p. 58 ( GKSM3.pdf (13 MB ) [accessed on May 3, 2020] Reprint of the edition from the Kaiser Wilhelm Institute for Flow Research , Göttingen, 1927).
- ↑ Oertel (2012), p. 92 f, see also Prandtl and Betz (1927), p. 58.
- ↑ Oertel (2012), p. 205.
- ↑ Rita Wodzinski (1999), p. 20.
- ↑ Oertel (2012), p. 217.
- ↑ Anderson, Eberhardt: Understanding Flight, 1st edition , pp. 35ff
- ↑ Oertel (2012), p. 223.
- ↑ Oertel (2012), p. 200.
- ^ Resonator podcast of the Helmholtz Association : Buoyancy (episode 71, October 23, 2015)
literature
- H. Oertel (ed.): Prandtl guide through fluid mechanics. Fundamentals and phenomena . 13th edition. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5 , p. 86 ff., 207 ff .
- Rita Wodzinski: How do you explain flying in school? Attempt to analyze various explanatory models. (PDF; 288 kB) Plus Lucis Subject Didactics, 1999, accessed on April 20, 2020 .
- JH Spurk: Fluid Mechanics . Springer Verlag, Heidelberg, Dordrecht, London, New York 2010, ISBN 978-3-642-13142-4 , doi : 10.1007 / 978-3-642-13143-1 ( limited preview in the Google book search).
- GK Batchelor: An introduction to fluid mechanics. Cambridge University Press, Cambridge 1994, ISBN 0-521-09817-3 .
- OP Craig, JR Pellam: Observation of perfect potential flow in superfluid. Phys. Rev., 108, pp. 1109ff, 1957, doi: 10.1103 / PhysRev.108.1109 .
- P. Eastwell: Bernoulli? Perhaps, but What About Viscosity? (PDF; 208 kB) In: The Science Education Review. 6 (1), 2007.
- H. Goldstein: Classical Mechanics. Wiley-VCH, Weinheim 2006, ISBN 978-3-527-40589-3 .
- Wolf-Heinrich Hucho: Aerodynamics of the blunt body . Physical fundamentals and practical applications. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1462-3 .
- J. Hoffren: Quest for an improved explanation of lift. AIAA 2001-0872.
- W. Send: Physics of Flying. In: Physical sheets. 57, No. 6, 2001.
- Klaus Weltner: A comparison of explanations of the aerodynamic lifting force. At the. J. Phys. 55 (1), pp. 50-54, 1987, doi: 10.1119 / 1.14960 .
- Klaus Weltner: flight physics . The physics of flight, fluid dynamics, rockets, satellites. BoD Books on Demand, Norderstedt 2016, ISBN 978-3-7412-1472-1 .
- David Anderson, Scott Eberhardt: Understanding Flight . 1st edition. McGraw-Hill, New York et al. 2001, ISBN 978-0-07-136377-8 .
- David Anderson, Scott Eberhardt: Understanding Flight . 2nd Edition. McGraw-Hill, New York et al. 2009, ISBN 978-0-07-162696-5 ( udocz.com [PDF] A Physical Description of Flight book excerpt).
- Holger Babinsky: How do wings work? In: Gary Williams (Ed.): Physics education . tape 38 , no. 6 . IOP Publishing (United Kingdom), November 2003 ( eng.cam.ac.uk [PDF; 370 kB ; accessed on August 4, 2017]).
























