viscosity
| Physical size | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Surname | dynamic viscosity | |||||||||
| Formula symbol | , | |||||||||
|
||||||||||
| Physical size | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Surname | kinematic viscosity | |||||||||
| Formula symbol | ||||||||||
|
||||||||||
The viscosity refers to the viscosity or tenacity of liquids and gases ( fluids ). The higher the viscosity, the thicker (less flowable) the fluid is; the lower the viscosity, the more fluid (flowable) it is.
Without further information, the resistance of the fluid to shear is meant. It is therefore referred to as the shear viscosity , to differentiate it from the elongation viscosity when elongated and the bulk viscosity when pressure is uniform. Furthermore, a distinction is made between dynamic viscosity and kinematic viscosity . The dynamic viscosity is the relationship between shear stress and velocity gradient. The reciprocal of dynamic viscosity is fluidity . The dynamic viscosity and kinematic viscosity are on the density directly related, .
Particles of viscous liquids are more strongly bound to one another and therefore less mobile; one speaks of internal friction . It results not only from the forces of attraction between the particles of the fluid ( cohesion ). With thinner fluids, the viscosity results from an impulse flow in the fluid. The viscosity of solids is comparatively high and therefore difficult to determine. Instead of viscosity, terms such as loss factor , storage and loss module are used.
The word viscosity goes back to the typically viscous juice of the berries in the plant genus mistletoe ( Viscum ). Bird glue was obtained from such mistletoes . "Viscous" means "tough like bird glue".
The viscosity appears in the calculation of the viscous stress tensor .
definition
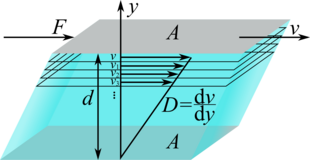
Imagine two panels of the surface arranged parallel to one another at a distance . Between these plates there is a liquid that adheres to both plates. In our imagination, the space with the liquid should be divided into layers. If the upper plate is now moved with the speed , the layer in the immediate vicinity also moves with the speed due to the adhesion . Since the lower plate is at rest, its neighboring layer is also at rest. The inner layers of liquid slide past each other at different speeds. The speed increases from the stationary plate to the moving one.
A tangential force exerts a tangential force on the layer below from the top layer adhering to the plate. This consequently moves with the speed. This layer in turn acts on the layer below and moves it with the speed
In the experiment it can be shown that in the ideal case the force that is necessary to move the upper plate is proportional to the area , the speed difference and inversely proportional to the distance between the plates :
- and and
This gives the equation
The constant of proportionality is the dynamic viscosity. The change in speed perpendicular to the direction of movement, i.e. the speed gradient
also referred to as or , is called deformation rate, shear rate or shear rate. With the shear stress
the connection arises
units
In the SI system of units, the following applies: A substance that is located between two plates has a dynamic viscosity of 1 N s / m ² if a force of 1 N is required with a plate size of 1 m² and a plate spacing of 1 m, to move the plates against each other at a speed of 1 m / s. The following applies to the physical unit of dynamic viscosity:
The following applies to the SI unit of the kinematic viscosity:
In practice, in addition to the Pa · s (pascal second), the thousandth part of the SI unit mPa · s (millipascal second) is used for media of low viscosity for the dynamic viscosity.
In the CGS system , the dynamic viscosity is measured in Poise (P), with 1 Ns / m² = 1 Pa · s = 10 Poise = 1000 Centipoise = 1000 cP = 1 kg / ms, and the kinematic viscosity in Stokes (St), 1 St = 10 −4 m 2 / s.
The Engler degree is an outdated unit of viscosity. This unit indicates the viscosity in comparison to water.
Viscosity of liquids
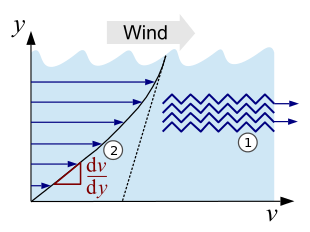
The effect of internal friction can be imagined in simplified form as the movement of two interlocked molecular layers lying on top of one another (see Fig. 1, point 1). The molecules slide past each other as they flow, and a certain amount of force is required to overcome the interlocking . The relationship between this force and the properties of the fluid in question defines the viscosity. This relationship can be recognized particularly well by the homologous series of alkanes (chain-like hydrocarbons), here the viscosity increases continuously with the chain length and thus with the increasing intermolecularly acting Van der Waals forces . In the case of the middle alkanes (from nonane , nine carbon atoms) it already has a value similar to that of water.
The viscosity can also be illustrated very well with the following example: if wind glides over the water of an ocean, this creates a movement of the water layer on the surface. The deeper you dive, the calmer the water becomes until you reach a point where there is no current. The individual layers of liquid move at different speeds , creating a speed gradient (see Fig. 1, point 2).
Newtonian fluids
If the fluid layers are very thin, the velocity curve is linear, as in the above derivation. This connection was assumed by Isaac Newton as early as 1687 :
"The resistance which arises from the lack of slipperiness originating in a fluid - other things being equal - is proportional to the velocity by which the parts of the fluid are being separated from each other."
"The resistance that arises from the lack of lubricity within a liquid is - provided that all other conditions remain the same - proportional to the speed with which the liquid particles are separated from one another."

1: Shear-thickening ( dilatant ) fluid
2: Newtonian fluid
3: Shear-thinning (pseudoplastic) fluid
4: Bingham-plastic fluid
5: Casson-plastic fluid
To the right is the shear rate and upwards the resulting one Shear stress applied.
Liquids that follow this linear relationship are therefore called Newtonian fluids . Is of dependent, is called the liquid as a non-Newtonian . With Newton's law of viscosity, laminar flow and temperature and pressure independence of the fluid properties are always assumed. The linear velocity profile shown in the shear stress-shear rate diagram is established for these substances (Fig. 3, curve 2: Newtonian fluid).
In the rheological models , the Newtonian behavior is represented by the Newton element, a damping cylinder similar to a shock absorber .
Non-Newtonian fluids
However, many substances do not follow this law, but show a behavior that is dependent on time or shear rate . A distinction is made between different types of deviation:
- Yield point , there must first be a certain minimum shear stress in order to achieve flow (plastic flow). This type of fluid is also called Bingham fluid called
- Structural viscosity / dilatance , the viscosity is not a constant, but changes with the shear gradient
- Thixotropy / rheopexy , this shows time-dependent structural changes, so that other viscosity values can be found depending on the length of time since the last flow movement.
In the general case, the shear gradient has to be calculated from the shear angle in the liquid and not from the velocity gradient. The ratio in this case is also called the apparent viscosity .
Viscoelastic materials can be described with the complex viscosity , which is based on a sinusoidal shear.
Typical non-Newtonian fluids are compound substances such as blood and ketchup . Since blood consists of both the solid substances of the hematocrit and the blood plasma , but the mixing ratio varies greatly, the viscosity also changes. With a high proportion of solid substances z. B. the performance in endurance sports is significantly increased, if too high through doping this can lead to death.
Temperature dependence
The dynamic viscosity of most liquids decreases with increasing temperature and can often be described using the Arrhenius-Andrade relationship :
With
- a material constant
- the activation energy (also place change energy )
- the general gas constant
- the absolute temperature .
For liquids close to (i.e. up to approx. 100 K above) the glass transition temperature , the WLF relationship usually applies . Here the very small free volume dominates, which in the vicinity of the glass transition temperature is much more dependent on the temperature than the chain mobility, which is behind the Arrhenius-Andrade relationship.
The dependence of the kinematic viscosity on the temperature is described in the case of oils by the viscosity index .
Especially for water, the viscosity in the temperature range between 0 ° C and 100 ° C can be determined using the formula given below. The temperature in the unit Kelvin is to be used. The value calculated with this corresponds to the dynamic viscosity in the unit Pa · s.
Measurement
The viscosity of liquids can be measured with a viscometer z. B. measured according to EN ISO 3219. A rheometer also makes it possible to determine other rheological properties, including those of solids. With both device types, the sample to be measured is placed in the gap between two bodies (e.g. two coaxial cylinders or two parallel plates) according to the viscosity definition. One part of the arrangement rotates or oscillates at a defined speed, while the other is at rest. The shear rate results from the geometry of the measuring arrangement and the speed of the moving part. The torque required to maintain the movement is measured, from which the shear stress and thus the viscosity can be determined.
The flow cup is a quick and simple, but also very imprecise method of determining viscosity .
Typical values

| substance | η in mPas (cP) |
|---|---|
| Water (5 ° C) | 1.52 |
| Water (10 ° C) | 1.297 |
| Water (20 ° C) | 1.00 |
| Water (25 ° C) | 0.891 |
| Blood (37 ° C) | 3 to 25 |
| Grape juice | 2 to 5 |
| olive oil | ≈ 10 2 |
| honey | ≈ 10 4 |
| syrup | ≈ 10 4 to 10 5 |
| Coffee cream | ≈ 10 |
| Ethylene glycol (20 ° C) | 20.81 |
| n -pentane (25 ° C) | 0.224 |
| n -hexane | 0.320 |
| n -heptane | 0.410 |
| Octane | 0.538 |
| Nonane | 0.711 |
| Decane | 0.920 |
| Dodecane | 1.52 |
| Paraffin oil | ≈ 10 2 to 10 6 |
| Benzene (25 ° C) | 0.601 |
| Diethyl ether | 0.240 |
| Diisopropyl ether | 0.33 |
| Ethanol | 1.19 |
| Acetic acid (80% at 25 ° C) | 2.31 |
| Glycerine (pure) | 1480 |
| chloroform | 0.56 |
| paint | ≈ 10 2 |
| Polymer melts | ≈ 10 3 to 10 13 |
| petroleum | 0.65 |
| Engine oil (150 ° C) | ≈ 3 |
| Engine oil (25 ° C) | ≈ 100 |
| Heavy oil RMA 30 (50 ° C) | 30th |
| Heavy oil RMK 700 (50 ° C) | 700 |
| Bitumen (depending on the type) | ≈ 10 7 to 10 14 |
| Asphalt (depending on the recipe) | ≈ 10 11 to 10 16 |
| mercury | 1.55 |
| Aluminum melt (700 ° C) | ≈ 2 |
| Glass (processing temperature) | ≈ 10 6 to 10 12 |
| Glass (room temperature) | ≈ 10 22 to 10 24 |
| Low-silica melt ( basalt lava ) at 1400 ° C | ≈ 10 0 to 10 1 |
| Silicate-rich melt ( Rhyolite lava ) at 1400 ° C | ≈ 10 5 to 10 7 |
| Rock salt | ≈ 10 18 to 10 21 |
- Color legend
- water
- Food
- Hydrocarbons
- Oxygen and chlorinated hydrocarbons
- Petroleum - "Products"
- Metals
- Mineral
- Others
- Remarks
- ↑ Unless otherwise stated, the values refer to the viscosity at 20 ° C. Millipascal seconds mPa · s are identical to the previously used unit centipoise cP.
- ↑ The values for blood probably apply to whole blood and vary greatly with the location in the respective blood vessels. In capillaries, the otherwise oblate (disc-shaped) red blood cells are prolate (elongated) deformed, which significantly reduces their viscosity. The finest capillaries are only as thick as individual blood cells, so that so-called plug flow occurs there, a viscosity can then no longer be meaningfully defined. In large vessels, red blood cells pile up to form long aggregates, which also significantly reduces their viscosity. (Yellowish) blood plasma is less viscous and even less colorless wound secretion or lymph that emerges from abraded skin . In the literature, the viscosity of blood in large vessels, with fast flow and with normal hematocrit is given as 3–4 mPa · s.
- ↑ There is a very wide range of viscosities for polymers, which essentially depends on the chain length and their branching structure, but also on the shear rate, since they have a structural viscosity. It is therefore not sensible to give a single viscosity value for polymers. The values mentioned serve only as an order of magnitude. Are produced e.g. B. silicone oils (PDMS) with defined viscosities between 0.6 mPa · s at 25 ° C and 1000 Pa · s at 27 ° C. However, polymer melts can also have much higher viscosities. In the case of a UHMW-HDPE (for hip joint implants ), viscosities beyond 10 10 Pa · s were measured at 150 ° C.
- ↑ a b c d e f g It must be emphasized that the specification of a viscosity value alone no longer makes sense for substances with viscosities above 10,000 Pa · s. For such substances, the complex shear modulus should be specified instead (Thomas Mezger: Das Rheologie Handbuch. Vincentz Network GmbH, 2007). The values given here serve only as a rough illustration of the order of magnitude.
- ↑ The viscosity of a crystalline solid is in principle infinite. Since irreversible deformation can still occur in the long term due to the inevitable defects in the crystallite, real crystalline substances still produce very large, but finite values.
Viscosity of gases
In the case of fluids with a low viscosity, the picture of internal friction “does not correspond to the physically correct ideas about molecular transport processes in fluids”. Instead, resulting here in the viscosity of a fluid momentum flux, which can be illustrated with the following image: The current paths in the flow are carried trains symbolizes that travel at different speeds in parallel side by side and are loaded with sandbags. The sandbags correspond to the fluid elements in the stream filament. People on the trains throw the sandbags at the other train, which equates to the accidental thermal movement of the fluid elements between the stream filaments. If a sack of the slower train lands on the faster one, the sandbag picks up the impulse that the faster train sends to it and thus slows down itself. Conversely, if a bag from the faster train lands on the slower train, the train takes up the impulse of the sandbag and thus becomes faster itself. This exchange of momentum slows down the faster train and accelerates the slower one.
Viscosity therefore represents a flow of momentum from a faster flowing stream to a slower one. In a continuum flow, the fluid elements exchange impulses via the voltages acting between them . Shear stresses occur between the streams flowing next to each other at different speeds , which macroscopically make themselves felt as viscosity.
appraisal
For gases, the viscosity can be estimated using a microscopic observation of the momentum flow:
with the free path for the gas particles, the mass of the gas particles , the mean particle velocity and the particle number density .
The viscosity of gases is independent of the pressure at low pressures (≈ 0.1 to 10 bar) . This applies as long as the free path is small compared to the dimensions of the vessel and large compared to the dimensions of the molecule. In other words: for a very thin or a very dense gas, the viscosity is again dependent on the pressure or the density of the gas.
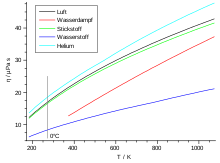
The viscosity is basically dependent on the temperature. The viscosity increases with increasing temperature, since the mean particle speed increases proportionally (see below). This behavior is exactly the opposite for most liquids. The following table lists the viscosities and free path lengths for some gases.
| Gas under normal conditions |
η in µPa · s | λ in nm |
|---|---|---|
| air | 18.2 | 59.8 |
| Oxygen (O 2 ) | 19.2 | 63.3 |
| Carbon dioxide (CO 2 ) | 13.8 | 39.0 |
| Nitrogen (N 2 ) | 16.6 | 58.8 |
| argon | 21.0 | 62.6 |
| neon | 29.7 | 124.0 |
| helium | 18.6 | 174.0 |
| Hydrogen (H 2 ) | 8.4 | 111.0 |
Kinetic gas theory
According to Hirschfelder, the viscosity of pure gases can be calculated with the help of the kinetic gas theory in a large temperature range (approximately from 200 to 3000 Kelvin).
Here is the molecular mass , the Boltzmann constant , the temperature, the Lennard-Jones impact diameter and the reduced impact integral, which depends on the reduced temperature . is the energy of the Lennard-Jones potential . Values for the Lennard-Jones parameters and the reduced shock integral are given in Chapter 11 of Lienhard's textbook on heat transfer. The reduced impact integral is defined in such a way that applies to an ideal gas in which particle interactions such as impacts from hard spheres are considered.
Physics of the friction tensor
The viscosity is based on the experiment according to which a force is required to maintain a shear flow. This force causes an exchange of momentum within the flow or with the edge, which is why it belongs to the category of surface forces. Continuum flows exchange momentum via mechanical stresses , with an increase in stress causing acceleration. In the continuum, the accelerating force can be formulated in the most general form as the divergence of a tensor :
where the component of the stress tensor is due to viscosity and is called a tough stress tensor or friction tensor . The Nabla operator forms the divergence div of the friction tensor here.
From the experiment it follows immediately that the friction tensor is a function of the spatial change in the flow velocity:
The operator grad forms the speed gradient from the speed . Since there is no momentum flow with homogeneous flow or the friction tensor does not contain any components that are independent of the velocity gradient. In Newtonian fluids , the stresses are linear in the velocity gradients, an assumption that is justified if the velocity gradient is small in terms of hydrodynamics .
Furthermore, no viscosity occurs if the flow is in rigid rotation ( with the distance vector from the axis of rotation), where the angular velocity is that results from the skew-symmetrical part of the velocity gradient, see kinematics in fluid mechanics . This skew-symmetrical component therefore has no influence on the stresses, which is why only the symmetrical component D of the speed gradient
Causes tension. The superscript T forms the transposition . With the further assumption of an isotropic liquid , the immediate material properties are described by scalar quantities. With this the friction tensor becomes:
It contains the Kronecker delta , the bulk viscosity , the first Lamé constant , the trace operator and is the unit tensor . The first term describes the viscosity through true-volume deformation (the tensor in the square brackets is non-marking or deviating ). The second term represents the viscosity through volume change. This term will disappear in the case of incompressibility , because then it is .
literature
- Joseph O. Hirschfelder, Charles F. Curtiss, Robert Byron Bird: Molecular Theory of Gases and Liquids . Wiley, 1964, ISBN 0-471-40065-3 .
- John H. Lienhard IV and John H. Lienhard V: A Heat Transfer Textbook . 3. Edition. Phlogiston, Cambridge 2005.
- Peter W. Atkins: Physical Chemistry / A. Höpfner (transl.) . 3., corr. Edition. Wiley-VCH, Weinheim 2002, ISBN 3-527-30236-0 .
- JM Dealy: Structure and Rheology of Molten Polymers . Hanser Fachbuchverlag, Munich 2006.
- C. Gabriel: Influence of the molecular structure on the viscoelastic behavior of polyethylene melts . Chair of Polymer Materials, Friedrich-Alexander University Erlangen-Nürnberg, Erlangen 2001.
- C. Piel, FJ Stadler, J. Kaschta, S. Rulhoff, H. Münstedt, W. Kaminsky: Structure-property relationships of linear and long-chain branched metallocene high-density polyethylenes and SEC-MALLS. In: Macromolecular Chemistry and Physics. 207 (1), 2006, pp. 26-38.
- Lothar Gehm: RHEOLOGY - Practice-oriented basics and glossary . Vincentz, 1998, ISBN 3-87870-449-6 .
- FR Schwarzl: Polymer Mechanics . Springer, Heidelberg / Berlin / New York 1993.
Web links
- Viscosity ( Memento from September 29, 2007 in the Internet Archive ) (PDF file; 157 kB)
- Video: Viscosity and NEWTON impulse transport - Why do you need more force when you stir faster? . Jakob Günter Lauth (SciFox) 2013, made available by the Technical Information Library (TIB), doi : 10.5446 / 15655 .
Individual evidence
- ↑ Overview of meanings: viscosity. Duden online, accessed on March 26, 2017 .
- ↑ viscosity. In: Lexicon of Physics. Spektrum Akademischer Verlag, accessed November 16, 2017 .
- ↑ Valentin Schröder: Examination trainer fluid mechanics . Vieweg & Teubner, 2011, p. 1 , doi : 10.1007 / 978-3-8348-8274-5_1 .
- ↑ Deepak Doraiswamy: The Origins of Rheology: A Short Historical Excursion . In: The Society of Rheology (Ed.): Rheology Bulletin . tape 71 , no. 2 , January 2002, p. 2 (English, rheology.org [PDF]).
- ↑ Alexander Y. Malkin, Avraam I. Isayev: Rheology. Concepts, Methods and Application. 2nd Edition. Toronto 2012.
- ↑ Arnd Krüger : 50 percent hematocrit - an arbitrary limit (NZZ, June 11, 1999), in: LimmatsharksZürich. online ( Memento from October 6, 2014 in the Internet Archive )
- ↑ tec-science: Viscosity of liquids and gases. In: tec-science. March 25, 2020, accessed on May 7, 2020 (German).
- ↑ Ralf Brandes, Rudi Busse: Circulation. In: Human Physiology. 31st edition. 2010, ISBN 978-3-642-01650-9 , pp. 576f.
- ↑ Nikos G. Tsierkezos, Ioanna E. Molinou: Thermodynamic Properties of Water + Ethylene Glycol at 283.15, 293.15, 303.15, and 313.15 K . In: Journal of Chemical & Engineering Data . tape 43 , no. 6 , November 1, 1998, ISSN 0021-9568 , p. 989-993 , doi : 10.1021 / je9800914 .
- ↑ R. Stenutz: diisopropyl ether.
- ↑ Nikolai I. Koskin, Mikhail G. Širkevič: elementary physics at hand: Definitions · Regulations · tables. 2013, ISBN 978-3-322-84038-7 , p. 41.
- ↑ Walter Blanke: Thermophysical substance quantities - heat and mass transfer. 2013, ISBN 978-3-662-10545-0 , p. 146.
- ↑ a b H-G. Scharbert: Introduction to the Petrology and Geochemistry of Magmatites. 1st edition. Vienna 1984, p. 60.
- ↑ F. Durst: Fundamentals of fluid mechanics . Springer, 2006, ISBN 3-540-31323-0 , pp. 62 f .
- ↑ LD Landau, EM Lifschitz: Textbook of theoretical physics. Volume VI: Hydrodynamics. Akademie Verlag, 1991.























![{\ displaystyle 1 \, {\ rm {N}} = [\ eta] \ cdot \ left ({\ frac {{\ rm {m}} ^ {2} \, {\ rm {m}}} {{ \ rm {m}} \, {\ rm {s}}}} \ right) \ Rightarrow [\ eta] = {\ frac {{\ rm {N}} \ cdot {\ rm {s}}} {{ \ rm {m}} ^ {2}}} = \ mathrm {\ frac {kg} {m \ cdot s}} = {\ rm {1 \, Pa \ cdot s}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be61a2806ed4c884df41aad9311a8253761841f)
![{\ displaystyle [\ nu] = {\ frac {\ rm {m ^ {2}}} {\ rm {s}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee08d4d423059ee6108c638250193bb53762c4ae)



































![{\ displaystyle \ mathbf {D}: = {\ frac {1} {2}} [\ operatorname {grad} {\ vec {v}} + (\ operatorname {grad} {\ vec {v}}) ^ { \ top}] = {\ frac {1} {2}} {\ begin {pmatrix} 2 {\ frac {\ partial v_ {x}} {\ partial x}} & {\ frac {\ partial v_ {x} } {\ partial y}} + {\ frac {\ partial v_ {y}} {\ partial x}} & {\ frac {\ partial v_ {x}} {\ partial z}} + {\ frac {\ partial v_ {z}} {\ partial x}} \\ & 2 {\ frac {\ partial v_ {y}} {\ partial y}} & {\ frac {\ partial v_ {y}} {\ partial z}} + {\ frac {\ partial v_ {z}} {\ partial y}} \\ {\ text {sym.}} && 2 {\ frac {\ partial v_ {z}} {\ partial z}} \ end {pmatrix} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e894ddaaa88dcc7c07a7740f5bb4aa169c03b58)
![{\ displaystyle \ mathbf {S} = 2 \ eta \ left [\ mathbf {D} - {\ frac {1} {3}} \ operatorname {Sp} (\ mathbf {D}) \ mathbf {1} \ right ] + \ zeta \ operatorname {Sp} (\ mathbf {D}) \ mathbf {1} \ quad {\ text {or}} \ quad S_ {ij} = \ eta \ left ({\ frac {\ partial v_ {i}} {\ partial x_ {j}}} + {\ frac {\ partial v_ {j}} {\ partial x_ {i}}} - {\ frac {2} {3}} \ delta _ {ij } \ sum _ {k = 1} ^ {3} {\ frac {\ partial v_ {k}} {\ partial x_ {k}}} \ right) + \ zeta \ delta _ {ij} \ \ sum _ { k = 1} ^ {3} {\ frac {\ partial v_ {k}} {\ partial x_ {k}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/134e960211b4c13004aa68e6c4717fb15eab644b)




