Rheological model
Rheological models describe the rheology , the science of the flow and deformation behavior of the materials, the relationship between the deformation of the body and this deformation causing external voltage . Since different materials show a significantly different behavior, different model bodies are necessary. For this purpose, the three idealized basic properties of elasticity , viscosity and plasticity are described with the basic model bodies borrowed from mechanics , spring, damping cylinder and friction block. More complex behavior that comes closer to reality can then be modeled by connecting several of these idealized basic elements in series and in parallel , analogous to ideal and real electrical components .
The behavior of the basic elements can be mapped mathematically with simple equations that represent the relationship between deformation and stress . The deformation can take place as stretching , compression , shear or torsion . Equations for the behavior of the composite model bodies can be derived from these basic equations.
The models thus make it possible to qualitatively and quantitatively describe, categorize and predict different flow and deformation behavior. In addition to rheology itself, they are used in many areas of technology and science, e.g. B. in materials science , in geology and in food technology .
Since they only allow statements about the macroscopic behavior of materials, but not about the causes for this, which lie in the respective material structure, they are part of the phenomenological rheology. Most of the model bodies were developed by their namesake from the end of the 19th to the middle of the 20th century.
Rheological phenomena
The need for different models becomes apparent when one looks at the different deformation behavior of materials: if you drop a rubber ball on a surface, for example , it deforms on impact and bounces back, i.e. it returns to its original shape (elastic behavior). A drop of water, on the other hand, runs under the influence of gravity after impact , i.e. it is permanently deformed (viscous behavior). A ball made of plasticine forms a kind of hemisphere on impact, which means it is permanently deformed without completely dissolving (plastic behavior). So-called bouncing putty made of silicone rubber , on the other hand, jumps back in the event of a rapid impact like a rubber ball, but gradually dissolves like a drop of liquid on a slow impact, thus showing a combination of different behaviors (so-called viscoelastic behavior).
In reality, however, practically all materials show elastic, viscous and plastic behavior at the same time, only the expression and the type of interaction of the individual properties differ. If the rubber ball were to be clamped in for a year, for example, it would also no longer fully assume its original shape after relaxation, but would show permanent deformation. So it does not show ideal elastic behavior. Even apparently clearly rigid materials such as hardened concrete or stone crawl , i.e. H. they gradually flow away over long periods of time.
The three basic models
Ideal elasticity
An ideally elastic body is characterized by the following properties:
- It reacts to an applied stress with an immediate deformation without a time delay.
- The amount of deformation is limited and proportional to the stress.
- If the tension no longer acts, the body moves back to its original position without delay, so the deformation is reversible.
- Hooke's law applies . The constant is the modulus of elasticity in the case of elongation, the modulus of compression in the case of compression or the modulus of shear in the case of shear or torsion.
These are the properties of an ideal solid and can be modeled by a spring, the so-called Hooke element.
Ideal viscosity
An ideally viscous body shows these characteristic properties:
- It reacts to an applied tension with a time-delayed deformation .
- The extent of the deformation is unlimited as long as the tension is applied.
- If the tension is no longer effective, the deformation remains, so the deformation is irreversible.
- The deformation speed is proportional to the applied stress. It applies . The constant here is the dynamic viscosity , which is usually considered in terms of shear, but also in terms of elongation (extensional viscosity ).
This describes an ideal liquid , also called Newtonian fluid . It can be modeled by a liquid-filled damping cylinder with a piston in it, similar to a shock absorber . The damping cylinder is assumed to be so large that the piston does not reach the limit of its mobility. This model is called the Newton element.
Ideal plasticity
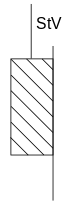
An ideally plastic body behaves as follows:
- As long as the stress is below the yield point , there is no deformation.
- If the flow limit is exceeded, the body deforms irreversibly at an undefined speed.
- So it applies
Thus, an ideally plastic body behaves below the flow limit like an ideally rigid solid, above the flow limit like a liquid with an infinitely low viscosity. This non-linear behavior can be modeled by a block that is located on a surface subject to friction. This too can only be set in motion after the static friction force has been exceeded . Such a model body is called a St. Venant element.
Composite model bodies
Series and parallel connection
More complex models that correspond more to reality can now be built from the basic models. If you connect model bodies in series, i.e. one behind the other, they all experience the same tension:
The expansion of the entire body is the sum of the expansion of the individual bodies:
When connected in parallel, the situation is exactly the opposite. The bodies experience the same stretch, the tensions add up:
Elastoplasticity
Many solids such as B. Steel show elastic behavior until reaching a yield point , above the yield point a permanent plastic deformation sets in. This behavior can be modeled by connecting a Hooke element in series with a St. Venant element, which results in the Prandtl body. Because of the series connection, the following applies:
Until reaching applies , so it affects only the Hooke element from. If the stress reaches the yield point, plastic deformation begins and the stress no longer increases.
But this behavior also represents an idealization. With real materials, the plastic deformation is not unlimited, but is limited by hardening processes . This can be taken into account by connecting another Hooke element in parallel .
For the plastic element has no influence, there is a parallel connection of two elastic elements that behave like a single Hooke element:
Plastic deformation sets in for . The tension in the strand with the St. Venant element now no longer increases and is constant . The following applies:
After resolving it results:
Even after the yield point has been exceeded, this model basically shows elastic behavior, but with a modified modulus of elasticity and reduced stress.
Viscoelasticity
A viscoelastic body exhibits viscous and elastic behavior at the same time. This corresponds to the combination of a Hooke with a Newton element. This effect often occurs with polymers and their melts.
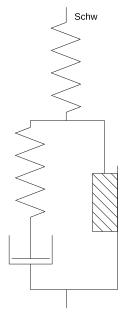
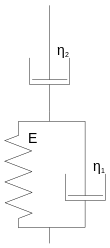
With the Kelvin body, also known as the Kelvin Voigt body, the two elements are connected in parallel. If an external tension is applied and maintained ( creep test ), the spring deforms elastically, but is slowed down by the Newton element so that the deformation occurs with a time delay. Over time, the deformation approaches the value given by the Hooke element. If the external force disappears, the body gradually springs back to its starting position. The deformation of the Kelvin body is limited and reversible, so it characterizes the behavior of a solid.
The behavior of the Kelvin body can be described mathematically by the differential equation
describe. With the boundary condition
the solution results for an applied tension
For applies , the deformation approaches the value of the pure elastic element.
Oskar Emil Meyer described the model for the first time in 1874, but because of later work by William Thomson (Lord Kelvin) and Woldemar Voigt it is called the Kelvin (Voigt) model.
The Maxwell body , the series connection of Hooke and Newton elements, represents a viscoelastic fluid. The deformation here is unlimited and irreversible due to the damping cylinder. The purely viscous behavior is supplemented here by an elastic component that is only noticeable immediately when the load is applied and unloaded: the spring tensions or relaxes immediately, while the viscous element takes time to deform. If the material is deformed up to a certain point and this deformation is then retained ( relaxation attempt ), the tension disappears over time, as the spring relaxes and its deformation is absorbed by the viscous element.
Because of the series connection, the following applies
With and results
The differential equation is derived from both sides
More complex behaviors can be represented by adding more elements. The Zener k or the Zener m body consists of the series connection of a Kelvin body with a Hooke body or the parallel connection of a Maxwell body with a Hooke element. They both describe solid-state behavior and have the advantage over the Kelvin body that they do not have an unrealistic, infinitely high stress peak at any high expansion speed.
The Zener k body reacts to a sudden load with a spontaneous deformation because of the spring connected in series . Then it shows the viscoelastic behavior of the Kelvin element. When the pressure is relieved, it also suddenly relaxes and then slowly returns to its starting position. A Zener m -body behaves qualitatively the same in the creep test. It is also possible to add further parallel Maxwell bodies with different moduli and viscosities to the Zener m model . This extended viscoelasticity model allows the decay behavior to be adapted more precisely to measured values.
| Zener k | Zener m |
|---|---|
 |

|
In the Lethersich and Jeffreys models , a Newton element is added instead of a Hooke . The two bodies thus represent the behavior of liquids. They differ from the Maxwell body in that the reversible deformation does not occur spontaneously, but is delayed by the added parallel damping cylinder.
The Burgers model was proposed in 1935 to model the behavior of asphalt and bitumen . It consists of a series connection of a Maxwell and Kelvin body. Polymers can also be described with the Burgers model. These often have a reversible entropy elasticity , which results from twisted polymer coils which are being pulled straight, and an irreversible deformation due to the breaking of or dislocations in molecular bonds. The former is embodied by the Kelvin body, the latter by the Maxwell body .
| Lethersich | Jeffreys | Burgers |
|---|---|---|
 |
 |

|
Visco (elasto) plasticity
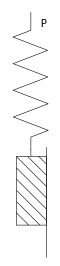
The combination of viscous and plastic behavior, i.e. a liquid that only flows after a limit voltage has been exceeded, is found in so-called Bingham fluids . Such a viscoplasticity can be idealized by connecting a St. Venant body in parallel with a Newton element. This is known as the Bingham body.
However, before reaching the yield point , Bingham fluids such as ketchup or toothpaste do not behave like a rigid solid, as would be the case according to the ideal Bingham model, but can already be elastically deformed. This can be represented by connecting a spring, the Bingham-Hooke model is obtained. After exceeding the flow limit, this body behaves like a viscoelastic liquid. The following applies:
This model thus combines all three basic properties, i.e. shows a visco-elasto-plasticity . In the literature, however, such behavior is often referred to simply as viscoplasticity .
Investigations on concentrated gelatin solution led to the development of the Schwedoff body in 1890 (see introduction). Its behavior is qualitatively similar to that of the Bingham-Hooke model.
The Schofield- Scott-Blair body represents a very extensive model from which all previous bodies can be derived if the corresponding viscosities are set to infinity or the corresponding modules are set to 0.
Deviations of the models from real behavior
The behavior modeled in this way still shows differences to the behavior of real materials, even with complex model bodies. There are several reasons for this. The Hooke and Newton elements assume a linear relationship between tension and deformation , or deformation speed . In reality, however, there is often a non-linear relationship . In particular with so-called non - Newtonian fluids , effects such as dilatancy and structural viscosity occur , i. H. the viscosity is no longer a constant, but in turn depends on the rate of deformation. The viscosity can change over time even if the deformation speed remains the same, which is referred to as thixotropy or rheopexy . Ultimately, the deformation behavior also depends on external influences, especially the temperature .
However, the model bodies can also be adapted to this by mathematically replacing the linear relationships with non-linear relationships. So one can get non-linear flow through the Eyring approach
instead of the linear approach . This takes into account both the temperature and the two material parameters and . The factor is the Boltzmann constant .
A mathematically simple and metrologically easy to implement procedure for the more exact characterization of viscoelastic substances consists in starting from a sinusoidally oscillating deformation ( vibration rheometry ). The viscous part is represented by the so-called loss module , the elastic part by the storage module . Both sizes can be selected depending on the frequency and amplitude. However, an at least approximately linear material behavior is still a prerequisite.
See also
Web links
Individual evidence
- ↑ a b c d e f g h Wilhelm Rust: Nonlinear finite element calculations . Contact, geometry, material. 2nd Edition. Vieweg + Teubner, 2011, ISBN 978-3-8348-8148-9 , chap. 5 Basics of the material models, p. 108–125 ( limited preview in Google Book search).
- ↑ a b Horst-Dieter Tscheuschner (Ed.): Basic features of food technology . 3. Edition. Behr's Verlag, Hamburg 2004, ISBN 3-89947-085-0 , chap. 4.5 Rheology of Food, p. 151–203 ( limited preview in Google Book search).
- ↑ a b Rheology. In: GeoDZ - Lexicon Geography, Lexicon Geology, Lexicon Geodesy, Topology & Geosciences. Arisleidy Stolzenberger-Ramirez, accessed June 28, 2013 .
- ↑ Hanswalter Giesekus: Phenomenological Rheology . An introduction. Springer, Berlin / Heidelberg / New York 1994, ISBN 978-3-642-57953-0 , chap. 1.2, 10, pp. 2, 239–340 ( limited preview in Google Book search).
- ↑ a b c d e f Manfred Pahl, Wolfgang Gleißle, Hans-Martin Laun: Practical rheology of plastics and elastomers . 4th edition. VDI-Verlag, 1995, ISBN 978-3-18-234192-5 , chap. 1. Basic terms and chap. 2. Rheological body , p. 1-56 .
- ↑ a b c d e f g h i j k Holger Meinhard: Rheological investigations on hardness impression experiments in the nanometer range . 1999, chap. 2. Rheological models, p. 4–14 ( uni-halle.de [PDF] Dissertation at the Mathematical-Natural-Scientific-Technical Faculty of the Martin Luther University Halle-Wittenberg).
- ↑ Thomas Mezger: Das Rheologie Handbuch . For users of rotation and oscillation rheometers. 2nd Edition. Vincentz Network, Hannover 2006, ISBN 978-3-87870-175-0 , chap. 5.2.2.1 The Kelvin / Voigt model , p. 89 .
- ↑ W. Lethersich: The mechanical behavior of bitumen . In: Journal of the Society of Chemical Industry . tape 61 , no. 7 July 1942, p. 101-108 .