Series connection
The series connection (also called voltage divider circuit depending on the application ) describes in electrical engineering the series connection of two or more components in a circuit in such a way that they form a single current path. Two components are therefore connected in series if their connection does not have a branch. The number of elements connected in series is arbitrary. As a counterpart to the series connection, there is another essential basic circuit, the parallel connection .
Analogous to the English term series circuit , the terms series circuit or connected in series are now often used instead of the term series circuit or the term connected in series . If two components are connected in series with opposite polarity ( e.g. Zener diodes ), this is also referred to as an anti- series connection . The term series connection was originally used for circuits in house installation that contain a series switch.
Properties of an electrical series connection
The series connection of several components has the following properties:
- The same electric current flows through all elements .
- The series connection of potential-free voltage sources makes it possible to generate a higher total voltage. This is z. B. used in batteries or solar cells .
- The series connection of consumers is susceptible to failures (in the sense of an interruption). If a single element breaks the electrical line or is removed from the line, the entire series fails. This is desirable with a fuse connected in series to the consumer . - In the event of a failure in the sense of a short circuit and with constant supply voltage, the voltage on the intact consumers increases.
- The series connection of relay contacts with the states "blocked" and "conductive" implements an AND function for the "conductive" state and an OR function for the "blocked" state. The latter is used for series-connected closed-circuit contacts in an alarm system.
Laws of series connections
| Linear electrical networks | |
|---|---|
| Ideal element | |
| Electrical component | |
| Series and parallel connection | |
| Network transformations | |
| Generator sets | Network sentences |
| Network analysis methods | |
| Two-port parameters | |
Ohm's law applies to ohmic resistances
- ,
wherein the electrical voltage , the electrical resistance and the electrical current is. This applies to constant quantities as well as effective values and instantaneous values for quantities that change over time.
The total resistance of a series connection increases with each additional ohmic consumer ; the total resistance is therefore always greater than the largest individual resistance. There is an exception in the series resonant circuit with AC voltage .
Amperage
The current intensity is identical for all consumers in the series connection in terms of frequency , phase angle and amplitude .
tension
The voltage is distributed to the individual consumers according to the Kirchhoff rule of meshes . The sum of the partial voltages is equal to the total voltage for resistive loads .
In the case of alternating voltage on components with reactance (coils, capacitors), the partial voltages add up to the total voltage in a Pythagorean way . Simply adding the amounts gives an incorrect value for the total voltage. In individual cases, the partial voltage on a component in the series connection can even exceed the total voltage (excessive voltage ).
power
With direct voltage, the total output is the sum of the outputs of each consumer:
With results
With AC voltage, the distinction between active power , reactive power and apparent power must be observed.
Series connections
Voltage sources
The total voltage generated when potential-free voltage sources (e.g. accumulators , transformer windings) are connected in series is the sum of the partial voltages, the sign of which must be observed according to the mesh rule.
If unlike poles are connected to one another, a higher total voltage is created, when connecting poles of the same name the differential voltage arises.
The internal resistances of the voltage sources add up regardless of the polarity.
Power sources
A series connection of ideal current sources of different sizes leads to unlimited high voltages between the current sources.
Resistances
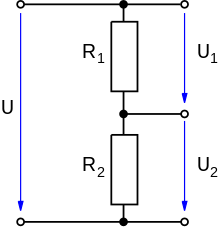
The figure on the right shows two resistors and with the same resistivity and total resistance
The following generally applies to series connections
A current with the same strength flows through all resistors . According to Ohm's law, this results in a voltage drop
The kirchhoff rule of meshes also applies to these
or adjusted according to the current strength
One example is the arrangement of incandescent lamps in a string of lights . With 16 identical lamps in series at 230 V, each one gets almost 15 V. An interruption of the circuit at one point (e.g. a lamp burns out) interrupts the current for all parts of the chain. Fairy lights lamps are therefore usually equipped with a current bridge that bypasses the failed element due to the higher voltage that occurs after the burnout.
If the conductance values are given instead of the resistance values , one obtains
Voltage divider
The voltage divider is a special application of series connection of resistors. It has a tap (branch) at the connection point and allows the total voltage to be divided in the ratio of the two resistors, provided that no current is drawn from the connection point. If (for example) a resistor is connected to the terminals for a consumer , a parallel connection is created from and , which reduces the voltage . With a real voltage measuring device as a consumer, the voltage is always measured lower than it is with open terminals.
With alternating voltage, voltage dividers can also be implemented with capacitors or coils, whereby Pythagorean addition has to be taken into account for mixed components.
Capacitors
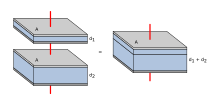
The figure shows two plate capacitors with the capacities and their series connection with the total capacitance. The relationship results from the conversion
In general, when capacitors are connected in series, the reciprocal value of the total capacitance is equal to the sum of the reciprocal values of the individual capacities:
or.
The formula corresponds to that for a series connection of the conductance values ( see above ).
If a charge is applied to a discharged capacitor with the capacitance , the voltage in accordance with
If a displacement current flows through the series connection (as a result of a switching process or with alternating voltage), it is the same in all components of the series connection and it applies the same charge to each capacitor. The total voltage on the series connection is divided according to
The capacitor with the smallest capacity receives the largest partial voltage.
The equation does not apply to DC voltage. In this case, the following considerations apply.
Voltage balancing
Connecting several capacitors of the same type in series requires balancing in the case of direct voltage in order to achieve an even distribution of the total voltage between the individual capacitors. Without this balancing, the capacitor with what happens to be the highest insulation resistance in the row receives the highest (possibly destructively high) DC voltage.
For voltage balancing with direct voltage, a resistor is usually connected in parallel to each capacitor. For example, if this is a power of ten less than the minimum insulation resistance of the capacitors guaranteed by the manufacturer, there is a symmetry error of up to 5% with two capacitors. However, the parallel resistances increase the losses. In most cases, however, for safety reasons, discharge resistors are required anyway for higher voltages (see also leakage resistance ), which can be used for this purpose.
When operated with AC voltage, the reactance values of the capacitors behave like their capacitance values. Balancing with parallel resistors is not necessary if the reactances are significantly smaller than the ohmic insulation resistances of the capacitors.
High-voltage capacitors often have what is known as an internal series connection : Instead of thick insulating film, several layers of metallized, thin insulating film are used. Such capacitors are more reliable and have a smaller overall volume than those with only one insulating layer, since the specific dielectric strength generally increases with decreasing thickness. The reason is the more homogeneous field distribution along the entire thickness of the insulating barrier.
Do the washing up
With the non-magnetically coupled series connection of coils with the inductances , the total inductance is the sum of the individual inductances, as is the case with resistors:
In the case of magnetically closely coupled inductances (for example a transformer ), the total inductance increases with the square of the number of turns. Two coils with the same inductance on a common core therefore provide four times the total inductance when connected in series.
Diodes
If diodes are operated in the forward direction and are connected in series in the same direction, their forward voltages add up .
If diodes are operated in reverse direction and are connected in series in the same direction, the total reverse voltage can be increased. The prerequisite is static and dynamic balancing (equal voltage distribution) both because of the leakage current and because of the junction capacitance . An exception applies if the diodes, due to their breakdown behavior, allow a series connection without additional measures (controlled breakdown, avalanche breakdown ). Examples are high-voltage rectifiers with selenium plates ( selenium rod ) or with silicon diode chips (rectifiers in high-voltage cascades for picture tubes or in voltage doubler circuits in microwave ovens ).
Transistors
The total reverse voltage or its switching voltage can be increased by connecting transistors in series . The prerequisite is static and dynamic balancing in order to achieve the same voltage distribution and to accommodate different switching times. You can do this with resistors and capacitors.
In special cases, MOSFETs can be connected in series without balancing if they are characterized by a controlled breakthrough (repeatedly permitted avalanche breakthrough ).
Gas discharges
Gas discharge lamps with the same nominal current can be connected in series. One example is the fluorescent tubes of neon advertising, which are operated up to a total voltage of 7.5 kV on a common stray field transformer .
To limit the current, gas discharge lamps always require series connection with a suitable ballast or series resistor .
lightbulbs
Incandescent lamps can only be connected in series if they have exactly the same nominal current - otherwise the incandescent lamp with the thinnest filament will burn out when it is switched on . The cause is the high inrush current due to the positive temperature coefficient of the resistor .
A related case is the series heating of electron tubes .
Loudspeaker (electro-dynamic)
Loudspeakers do not represent pure ohmic resistances for the audio signal (e.g. 4 or 8 Ω, these are only nominal values), but a complex load , consisting of additional resonant circuits, which are transferred from the acoustic-mechanical world to the electrical area via the converter function (back) to be converted. The main reasons for this are the basic resonance ( mass-spring system ) of all drivers, the inductance of the voice coils and - especially important in multi-path systems - the crossovers. Due to other tasks, these can only rarely be designed in such a way that they form a constant impedance (alternating current resistance) in total.
For this reason, it makes no sense to connect different loudspeakers in series. The result is mutual sound (discoloration) and undesirable uneven distribution of the load on the individual loudspeakers.
On the other hand, connecting two or more loudspeakers of the same type in series does not pose a problem in terms of sound or electrical connection values. However, there is a multiplication of the impedance. If the impedance is too high, the maximum usable output power of the audio output stages is reduced (voltage adjustment, high damping factor). B. 4 or 6 or 9 loudspeakers offers a combined series-parallel connection, so that the impedance of the overall circuit remains the same.
See also
Web links
Individual evidence
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary
- ↑ Wolfgang Böge, Wilfried Plaßmann (ed.): Vieweg-Handbuch Elektrotechnik. Vieweg, Wiesbaden 2007, ISBN 978-3-8348-0136-4 . Cape. II.3, p. 257
- ↑ Joachim Specovius: Basic course in power electronics: components, circuits and systems. Vieweg + Teubner, 4th ed., 2010, p. 26