Specific resistance
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | specific resistance | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
| See also: electrical conductivity | ||||||||||||||||
The specific resistance (short for specific electrical resistance or resistivity ) is a temperature-dependent material constant with the symbol (Greek rho ). It is mainly used to calculate the electrical resistance of a ( homogeneous ) electrical line or a resistance geometry. The SI derived unit for this purpose is . The unit (abbreviated to dimensions) is usually used for scientific purposes .
The reciprocal of the specific resistance is the electrical conductivity .
Cause and temperature dependence
Two components are responsible for the specific electrical resistance in pure metals , which are superimposed according to Matthiessen's rule :
- Collisions of the charge carriers (here electrons ) with lattice vibrations ( phonons ); this proportion depends on the temperature, and
- Collisions of the charge carriers (here electrons) with impurities, defects and lattice construction defects ; this proportion does not depend on the temperature, but on the concentration of the lattice defects.
The temperature-dependent portion of the specific resistance is approximately linear for all conductors in a limited temperature range:
where α is the temperature coefficient , T the temperature and T 0 any temperature, e.g. B. T 0 = 293.15 K = 20 ° C, at which the specific electrical resistance ρ ( T 0 ) is known (see table below).
Depending on the sign of the linear temperature coefficient, a distinction is made between PTC thermistors ( positive temperature coefficient of resistance , PTC) and thermistors ( negative temperature coefficient of resistance , NTC). The linear temperature dependence is only valid in a limited temperature interval. This can be comparatively large with pure metals. In addition, you have to make corrections (see also: Kondo effect ).
Pure metals have a positive temperature coefficient of specific electrical resistance of around 0.36% / K to over 0.6% / K. With platinum (0.385% / K) this is used to build platinum resistance thermometers .
The specific electrical resistance of alloys is only slightly dependent on the temperature, here the proportion of imperfections predominates. This is used for example with constantan or manganin in order to obtain a particularly low temperature coefficient or a temperature-stable resistance value.
Specific resistance as a tensor
For most materials, the electrical resistance is direction-independent ( isotropic ). A simple scalar quantity is then sufficient for the specific resistance, i.e. a number with a unit.
Anisotropy in electrical resistance is found in single crystals (or multi- crystals with a preferred direction) with less than cubic symmetry . Most metals have a cubic crystal structure and are therefore isotropic. In addition, one often has a multicrystalline shape without a pronounced preferred direction ( texture ). An example of anisotropic specific resistance is graphite as a single crystal or with a preferred direction. The specific resistance is then a 2nd level tensor , which links the electric field strength with the electric current density .
Relationship with electrical resistance
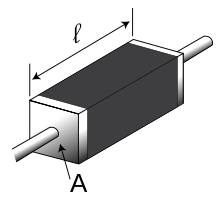
The electrical resistance of a conductor with a constant cross-sectional area over its length ( section perpendicular to the longitudinal axis of a body) is:
where R is the electrical resistance , ρ is the specific resistance, l is the length and A is the cross-sectional area of the conductor.
Consequently, one can determine from the measurement of the resistance of a conductor section of known geometry:
The cross-sectional area A of a round conductor (for example a wire ) is calculated from the diameter d as follows:
The prerequisite for the validity of this formula for the electrical resistance R is a constant current density distribution over the conductor cross-section A , that is, the current density J is the same at every point of the conductor cross-section . This is approximately the case when the length of the conductor is large compared to the dimensions of its cross-section and the current is a direct current or a low frequency. At high frequencies the skin effect and at inhomogeneous high-frequency magnetic fields and geometries the proximity effect lead to an inhomogeneous current density distribution.
Further parameters that can be derived from the specific resistance are:
- the sheet resistance (sheet resistance of a resistive layer); Unit or
- the resistance per length of a wire or cable; Unit / m
Classification of materials
In the case of electrical conductors, the specific resistance is often given in the form that is more descriptive for wires . Furthermore is also common.
The following applies:
The specific resistance of a material is often used for classification as a conductor , semiconductor or insulator . The distinction is made based on the specific resistance:
- Head :
- Semiconductors :
- Insulators or non-conductors :
It should be noted that this classification has no fixed limits and is therefore only to be regarded as a guide. This is why the literature also contains information that can differ by up to two orders of magnitude. One reason for this is the temperature dependency of electrical resistance, especially in semiconductors. A classification based on the position of the Fermi level makes more sense here.
Specific resistance of different materials
| material | Specific resistance in Ω · mm 2 / m |
Linear resistance temperature coefficient in 1 / K |
|---|---|---|
| Battery acid | 1.5e4th | |
| aluminum | 2.65e-2 | 3.9e-3 |
| Alumina | 1e18th | |
| Amber | 1e22nd | |
| lead | 2.08e-1 | 4th.2e-3 |
| blood | 1.6the6th | |
| Stainless steel (1.4301, V2A) | 7th.2e-1 | |
| iron | 1.0e-1 to1.5e-1 | 5.6the-3 |
| Adipose tissue | 3.3e7th | |
| Germanium (foreign content <10 −9 ) | 5e5 | |
| Glass | 1e16 to 1e21st | |
| mica | 1e15 to 1e18th | |
| gold | 2.214e-2 | 3.9e-3 |
| graphite | 8the0 | -2e-4th |
| Rubber (hard rubber) (material) | 1e19th | |
| Wood (dry) | 1e10 to 1e16 | |
| Saline solution (10%) | 7th.9e4th | |
| carbon | 3.5e1 | -2e-4th |
| Constantan | 5e-1 | 5e-5 |
| Copper (pure, "IACS") | 1.721e-2 | 3.9e-3 |
| Copper (electrical cable) | 1.69e-2 to1.75e-2 | |
| Copper sulfate solution (10%) | 3e5 | |
| Brass | 7the-2 | 1.5e-3 |
| Muscle tissue | 2e6th | |
| nickel | 6th.93e-2 | 6th.7the-3 |
| NickelChrome (alloy) | 1.32 | until 1e-6th |
| paper | 1e15 to 1e17th | |
| platinum | 1.05e-1 | 3.8the-3 |
| Polypropylene film | 1e11 | |
| porcelain | 1e18th | |
| Quartz glass | 7th.5e23 | |
| mercury |
9.412e-1 (0 ° C) 9.61e-1 (25 ° C) |
8th.6the-4th |
| Hydrochloric acid (10%) | 1.5e4th | |
| sulfur | 1e21st | |
| Sulfuric acid (10%) | 2.5e4th | |
| silver | 1.587e-2 | 3.8the-3 |
| steel | 1e-1 to2e-1 | 5.6the-3 |
| titanium | 8the-1 | |
| Water (pure) | 1e12 | |
| Water (typ. Tap water) | 2e7th | |
| Water (typ. Sea water) | 5e5 | |
| tungsten | 5.28e-2 | 4th.1e-3 |
| tin | 1.09e-1 | 4th.5e-3 |
example
It is the length of an unknown metal wire , its cross-section , the test voltage and the current was measured.
Find the specific electrical resistance of the wire material.
It applies
After being rearranged, it results
and with the values will
The specific resistance of the examined wire determined in this way suggests that it could be copper .
literature
The recommended standard work for tabular data on the specific (electrical) resistance is:
- David R. Lide: CRC Handbook of Chemistry and Physics : A ready-reference book of chemical and physical data . 90th edition. CRC Taylor & Francis, Boca Raton FL 2009, ISBN 978-1-4200-9084-0 .
- Kohlrausch - Table 8.26 Specific electrical resistance of metals at 0 ° C, temperature coefficient 0-100 ° C (PDF)
Web links
- Virtual experiment on specific resistance
- Conductivity and Resistivity Values for Iron & Alloys . (PDF; 116 kB) Collaboration for NDT Education, March 2002 (table with the specific resistance of many alloys).
Individual evidence
- ^ Siegfried Hunklinger: Solid State Physics . Oldenbourg Verlag, 2009, ISBN 978-3-486-59045-6 , pp. 378 (semiconductor: ρ = 10 −4 … 10 7 Ω · m).
- ^ Karl-Heinrich Grote, Jörg Feldhusen : Dubbel: Paperback for mechanical engineering . Springer, 2011, ISBN 978-3-642-17305-9 , pp. V 14 (semiconductor: ρ = 10 −3 … 10 8 Ω · m).
- ↑ Wolfgang Bergmann: Materials technology . 4th edition. tape 2 . Hanser Verlag, 2009, ISBN 978-3-446-41711-3 , pp. 504 (semiconductor: ρ = 10 −5 … 10 9 Ω · m).
- ↑ Peter Kurzweil, Bernhard Frenzel, Florian Gebhard: Physics formula collection: with explanations and examples from practice for engineers and natural scientists . Springer, 2009, ISBN 978-3-8348-0875-2 , pp. 211 (semiconductor: ρ = 10 −5 … 10 7 Ω · m).
- ^ Horst Czichos, Manfred Hennecke: The engineering knowledge . with 337 tables. Springer, 2004, ISBN 978-3-540-20325-4 , pp. D 61 (semiconductor: ρ = 10 −5 … 10 6 Ω · m).
- ↑ Ekbert Hering, Karl-Heinz Modler: Basic knowledge of the engineer . Hanser Verlag, 2007, ISBN 978-3-446-22814-6 , pp. D 574 (semiconductor: ρ = 10 −4 … 10 8 Ω · m).
- ↑ a b c d e f g h David R. Lide (Ed.): CRC Handbook of Chemistry and Physics . 90th edition. (Internet version: 2010), CRC Press / Taylor and Francis, Boca Raton, FL, Properties of Solids, pp. 12-41-12-42.
- ↑ Stainless Steels Chromium-Nickel ( Memento from February 17, 2004 in the Internet Archive ; PDF)
- ↑ Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbook of electrical engineering: Basics and applications for electrical engineers. Vieweg + Teubner, 5th edition, 2009, p. 231.
- ↑ Specifications of the manufacturer AURUBIS: Pure copper (100% IACS) = 0.01721 ( Memento of the original from April 28, 2014 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Electro copper E-Cu58 ident. Cu-ETP1 , 1.69e-2 to1.75e-2 , occasionally ≈1.9e-2 Ω mm2/ m
- ↑ Data sheet of an alloy suitable for precision resistors
- ↑ LF Kozin, SC Hansen, Mercury Handbook, Royal Society of Chemistry 2013, page 25

![[\ rho] = \ mathrm \ tfrac {\ Omega \ cdot mm ^ 2} {m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/780127c4f8ef1ee1cb4c7c8d90aa1b54ad544f26)
![[\ rho] = \ Omega \ mathrm m](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e63e5c7f1a47b84eaf597b78d21b5cda617c1c1)