Electrical resistance
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Electrical resistance | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
In electrical engineering, electrical resistance is a measure of the electrical voltage required to allow a certain electrical current to flow through an electrical conductor ( component , circuit ). Here are equal sizes to use or instantaneous values at varying over time sizes.
When the voltage is counted from a connection point A to a connection point B, the current in the conductor is counted positive as it flows from A to B; the resistance cannot be negative.
The symbol for electrical resistance is usually derived from the Latin resistere for "to resist". The resistance has the SI unit ohm , its symbol is the Ω (large omega ).

Voltage and current have the same sign in these counting directions
Historical relationships are dealt with in the article " Ohm's Law ".
Ohmic resistance
Fundamental connections
An electrical resistance is an ohmic resistance if its value is independent of the voltage, the strength of the current and any other parameters . Ohm's law applies to such a resistor. If the voltage is plotted against the current intensity in a line diagram, an ohmic resistance results in a straight line through the origin ; the voltage drop across a component with an ohmic resistance is proportional to the current intensity in the resistance with the proportionality factor ; this is also the rise of the straight line:
As an approximation and with restrictions, an ohmic resistance can be implemented by a component, in the simplest case a metal wire. This is usually also referred to as a resistance - see resistance (component) .
If the current in the resistor causes a voltage drop , electrical energy is converted into thermal energy .
The reciprocal value of the ohmic resistance, i.e. the proportionality factor between current strength and voltage, is called the electrical conductance of a conductor. The following applies:
Calculating the resistance of a conductor
The ohmic resistance of a body can be calculated from its geometric dimensions and a material constant, the specific resistance .
The following applies to a straight conductor with a constant cross-sectional area and length , through which there is a longitudinal flow :
The specific resistance itself is generally dependent on the temperature and possibly other variables.
Influence Effects
- An influence of the voltage on the electrical resistance has to be considered in the case of high voltages and high resistance values in the order of magnitude , in new developments of measuring resistors up to two powers of ten less. In many cases it is in the case of non-linear resistances , e.g. B. semiconductors to observe; see below . The influence of voltage on the resistance of an incandescent lamp results indirectly from the influence of temperature.
- With many resistors, the frequency only has an influence at higher frequencies due to the skin effect , but even at 50 Hz, the influence in the thick conductor cables of high-voltage overhead lines has an effect . In the case of alternating current resistors, a frequency influence can also be observed at low frequencies; see below . To distinguish it, the frequency-independent component of the resistance is also referred to as the direct current resistance .
- The influence of temperature must often be taken into account, as described below:
The above equation for the DC resistance of a straight conductor is then replaced by, for example
| Examples of specific resistance and temperature coefficient at 20 ° C |
||
|---|---|---|
| material | in Ω mm 2 / m | in 1 / ° C |
| silver | 16e-3 | 3.8the-3 |
| copper | 17the-3 | 4th.3e-3 |
| nickel | 70e-3 | 6th.6the-3 |
| Nickel-chromium | 13e-1 | until 1e-6th |
The index denotes the Celsius temperature to which the quantities apply. In table books the usual reference temperature is 20 ° C. The values depend on the degree of purity as well as thermal and mechanical treatment; therefore the table values are only to be understood as guidelines.
The influence of the temperature on the resistance can be represented in simple cases with the linear temperature coefficient and the temperature difference . Then the relationship is described by a linear equation
- at
For most applications with metallic materials and temperature ranges that are not too large, this linear approximation is sufficient; otherwise terms of a higher order are to be included in the equation. (For an example with summands up to the fourth power, see platinum in the article Resistance thermometer .)
Depending on whether the resistance value increases or decreases with increasing temperature, a distinction is made between
- NTC thermistors ( Negative Temperature Coefficient ; resistance value drops) and
- PTC thermistors or PTC ( Positive Temperature Coefficient ; resistance value increases). Generally all metals are PTC thermistors.
In measurement and control technology , the temperature dependency of electrical resistance is used as a measurement effect , for example in resistance thermometers , other temperature sensors , thermal anemometers or inrush current limiters .
There are also various special alloys that are characterized by a specific electrical resistance that is approximately constant over a wide temperature range, as is required for a measuring resistor .
AC resistance
presentation
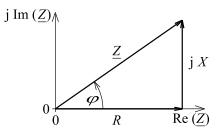
At a purely ohmic linear resistor through which alternating current flows, voltage and current have the same phase angle . If, however, the resistance changes as a function of the frequency and the phase position shifts, a component has been added to the ohmic part of the resistance , which reacts to changes in voltage or current with a delay. In the case of a sinusoidal curve of voltage and current intensity, the quotient of the amplitudes or effective values is referred to as impedance . In the complex AC calculation, the impedance is combined with the phase shift angle as impedance or complex resistance :
In another representation, the two components in the complex plane are combined at right angles to one another :
In it are as effective resistance and a reactance referred. The effective resistance, which does not work in a phase-shifting manner, is also referred to as the ohmic component of the impedance.
If the voltage and the current strength are represented as sinusoidal quantities with the frequency or the angular frequency in the complex plane by pointers and , this results from the inclusion of Euler's formula
With
Causes of the complex resistances
For a coil with inductance, the following applies
Due to a voltage, the current strength increases over time. With alternating current this follows with a delay. With the approach in complex notation and as above, after the differentiation results
This is referred to here as inductive reactance
Together with the factor , the result means that an inductance acts like a phase-rotating reactance for sinusoidal alternating quantities. With results
The impedance of an inductance is a resistance proportional to the frequency , but otherwise linear .
The same applies to a capacitor with the capacitance
Due to a current, the voltage increases over time. With AC voltage, this follows with a delay. In complex notation and after integration results
This is called capacitive reactance here
Together with the factor , the result means that a capacitance for sinusoidal alternating variables acts like a phase-rotating reactance. Here is
The impedance of a capacitance is inversely proportional to the frequency , but otherwise linear.
Conversions
By comparing the representations
surrender
- (Effective resistance),
- (Reactance)
and for the impedance :
- or
and for the phase shift angle between and :
special cases
- The following applies to:
-
.
- For is and ;
- for is and .
- The following applies to:
- .
Interconnection, equivalent resistor
The equivalent resistance is the complex electrical resistance that has the same resistance as an electrical circuit or the part of an electrical circuit that it replaces. An equivalent resistance can illustrate the behavior of complex electrical arrangements and enable calculation; see also equivalent circuit diagram .
AC resistances that actually occur can often be described by a series connection or parallel connection of an ohmic resistor with an inductance or with a capacitance. Which of the images is used is a question of a better approximation to reality with variables that are as frequency-independent as possible and the expediency for mathematical treatment.
On closer inspection, however, every capacitor also has a small inductive component, just as a coil also has a capacitive component. Even a piece of wire must be described exactly with , and ; see also line covering . This is particularly evident when the components with their geometric dimensions come in the range of the wavelength of the applied alternating voltage; then they have an inductance and capacitance which cannot be neglected. If necessary, they become an oscillating circuit , an example being the antenna . The ends of these can be seen as capacitor plates, the wire between them as a coil.
If an ohmic resistor and a reactance are connected together, the rules below for series and parallel connection can be applied in complex notation.
If a capacitive and an inductive impedance are connected together, a resonant circuit is created if the ohmic load is sufficiently small ; the series and parallel connection and the other consequences are dealt with under this heading.
Locus
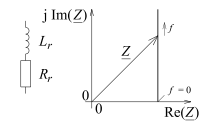
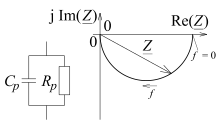
The locus curve is a clear aid for the analysis and description of circuits with alternating current resistances .
Complex quantities can be represented by pointers in the complex plane. If the complex quantity is a function of a (real) parameter and if this parameter is varied, the tip of the pointer shifts. A line through all conceivable pointer tips is called a locus.
The pictures show locus curves of the impedance as a function of the frequency for the specified circuits. In the case of an RL or RC series circuit with an ohmic resistance that is independent of the frequency, the active component of the impedance is also independent of the frequency. With the corresponding parallel connection, the active and reactive components of the impedance are clearly both dependent on the frequency.
Series and parallel connection
Series connection
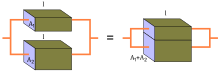
If ohmic resistors are connected in series, the resistances add up:
This can be illustrated by the series connection of two resistors that differ only in length .
The series connection results in a resistance body of length . Then:
If the resistances ( ) are the same , the total resistance is as large as the individual resistance multiplied by the number of resistors:
The resistance of a series connection is always greater than the largest individual resistance. There is an exception for AC resistors in a series resonant circuit .
Parallel connection
If ohmic resistors are switched next to one another, the conductance values or the reciprocal resistances add up:
This can be illustrated by the parallel connection of two resistors that only differ in their cross-sectional area .
The parallel connection results in a resistance body of the cross-sectional area . Then:
and moved
There is an alternative notation for parallel connection with the parallel symbol :
The following applies in particular to two parallel resistors:
If the resistances are the same, the total resistance is as large as the individual resistance divided by the number of resistors:
The resistance of a parallel connection is always smaller than the smallest individual resistance. There is an exception for AC resistors in the parallel resonant circuit .
Differential resistance
In the case of non-linear current-voltage characteristics - such as those of diodes - the quotient is different for each current-voltage pair. In this case Ohm's law does not apply and one cannot speak of a linear resistance . However, small changes in voltage are approximately proportional to the small changes in current intensity associated therewith. The quotient of a small change in voltage and the associated change in current intensity at a certain voltage is called the differential resistance . In a diagram in which is plotted over , it corresponds to the slope of the tangent at the point of the characteristic curve.
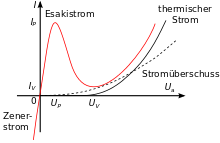
Negative differential resistance
The differential resistance can be negative in a part of the characteristic curve, so that the current intensity decreases with increasing voltage or the current intensity increases with decreasing voltage. Pictured is in the field U P < U < U V the case. A negative differential resistance can be used to excite (de-dampen) resonant circuits or to generate breakover oscillations ( oscillator ). The negative differential resistance occurs, for example, in gas discharges or in components such as avalanche and tunnel diodes , in simple electronic circuits such as the lambda diode , but also in more complex modules such as e.g. B. Switching power supplies on the input side.
Positive differential resistance
With positive differential resistances, the current strength increases with increasing voltage. All actually existing circuit elements have a part of their characteristic curve, but always for very large values, a positive differential resistance. Most elements in circuit technology have an exclusively positive differential resistance.
Examples: real resistance, diode , Zener diode , all semiconducting ceramics.
The electrical resistance in the particle model
The physical description uses the idea that the valence electrons in the metal behave like a gas ( electron gas ). In the simplest model, the metal forms a positively homogeneously charged volume in which the electrons can move freely. The atomic cores, which consist of the atomic nucleus and the more strongly bound electrons on the deeper, fully occupied shells, are embedded in this volume.
Without external electrical voltage, the electrons move in a disordered manner in the metal (see Brownian movement ). If you now apply a voltage, the free electrons are accelerated by the electric field in the direction of the field lines . An electric current flows.
On their way through the metal there is elastic collision of the electrons with other electrons, the atomic trunk and phonons . The electrons give off energy to their collision partners, are scattered and accelerated again by the electric field. The electrons are permanently slowed down by this interaction and an average flow velocity is established.
The energy transferred to the atomic cores or phonons during these collisions leads to a greater natural oscillation around their equilibrium position, their temperature increases. The stronger vibrations increase the cross-sectional area for possible impacts, the number of which increases with increasing temperature and increases resistance ( PTC thermistor ). The conduction process in NTC thermistors cannot be fully explained with this model, since with increasing temperature a significant generation of charge carriers occurs, which superimposes the process just described.
At very high temperatures, at which the atoms of the material are ionized ( plasma ), every substance is electrically conductive, as the electrons previously bound are now available for charge transport. Conversely, metals and oxides are known for which the electrical resistance disappears at very low temperatures below a specific transition temperature : superconductors have no ohmic resistance with direct current, current flows without losses at this low temperature.
The thermal movement of the electrons creates a temperature-dependent noise current, which is referred to as resistance noise .
Hall effect
The Hall resistance indicates the ratio of voltage to current of a Hall element at a certain magnetic flux density, this voltage occurring across the current density . It characterizes the Hall element or the magnetic flux density, but has nothing to do with the electrical resistance of this Hall element.
The quantum Hall effect is expressed by the fact that at low temperatures and strong magnetic fields the voltage that occurs perpendicular to the current density does not increase linearly with the flux density, as in the classic Hall effect, but in steps. This phenomenon leads to a universal natural constant, the " Von Klitzing constant " from the dimension of resistance. Since Von Klitzing's constant can be measured relatively easily, it has been proposed to use it as a standard for measurements of electrical resistance.
Web links
- Experiments and exercises on electrical resistance (Wayback Machine Archive) ( Memento from February 1, 2017 in the Internet Archive ) ( LEIFI )
- Preservation and representation of the unit of electrical resistance ohm . Exhibit information sheet from the Physikalisch-Technische Bundesanstalt, Hannover Messe '82, April 21, 1982
Individual evidence
- ↑ EN 80000-6, Quantities and Units - Part 6: Electromagnetism , 2008; Entry 6-46.
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary , entry 131-12-04.
- ↑ Wolfgang Gruhle: Electronic measurement: Analog and digital signal treatment. Springer, 1987, p. 95
- ↑ Data sheet for high voltage resistors
- ↑ data sheet for Cu 99.9%
- ↑ Data sheet for Ni 99.98%
- ↑ Data sheet of an alloy suitable for precision resistors