Ohm's law
The Ohm's law states that: The strength of the current flowing through an object electric current is proportional to the electric voltage . More precisely: If the electrical resistance defined as the quotient of voltage to current strength is constant, i.e. independent of voltage and current strength, Ohm's law applies to the object; the object then has an ohmic behavior .
The designation of the law honors Georg Simon Ohm , who was the first to conclusively prove this connection for some simple electrical conductors.
In fact, the assumption of constant resistance only applies to a narrow range and only for some substances - in particular for metals at constant temperature. In reverse of the original experience, Ohm's law is now a requirement for a resistance called ohmic . The law is the basis for understanding the relationships between current strength and voltage in electrical circuits and, together with some other ideal components, the basis for every theoretical and mathematical treatment and for circuit simulation .
description
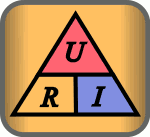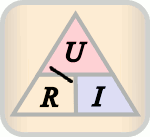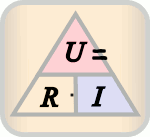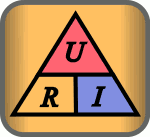
The ratio of an electrical voltage applied to an electrical conductor (resistance) to the strength of the electrical current flowing through it is defined as the electrical resistance value, which is denoted by the symbol . Instantaneous values are to be used for variables that change over time. The ratio must not be a function of time. Ohm's Law considers the resistance as one of and independent constant and is thus an idealization. The following applies:
A passive electrical circuit with a proportionality between current strength and voltage has an ohmic behavior and has a constant electrical resistance, which is called ohmic resistance . Even with non-ohmic behavior, the variable resistance is defined as a ratio , but then there is a dependency of the resistance z. B. from the tension before. An incandescent lamp and a diode, for example, behave non-linearly. The term differential resistance , which indicates the relationship between a small change in voltage and the associated change in amperage, can be helpful for describing such behavior .
The equation that follows from Ohm's law can be represented in three ways (through equivalence transformations ):
In many cases, the definition of resistance alone as the quotient of voltage and current strength is referred to as "Ohm's law", although the constancy of resistance is the core statement of Ohm's law.
Local approach
In a local viewing Ohm's law by the linear relationship between the is current density - vector field (in components ) and the electric field strength vector field (in components ) with the electrical conductivity - Tensor (in components ) as a transport coefficient described below:
- , or in components
where the indices m and n run from 1 to 3 ( x , y and z ).
In isotropic materials the tensor can be replaced by a scalar , and the following applies:
If the movement of the free electrons is considered analogous to the disordered movement of molecules in an ideal gas, the constancy of the electrical conductivity appears plausible: the counting density of the electrons is then constant within the conductor. The following applies to the mean speed of the electrons:
The mean distance between two collisions with ions in the metal is covered in a typical time :
During this time the electrons experience an acceleration
by the applied electric field, where is the elementary charge and the electron mass . The electrons thus reach a drift speed with . Substituting this into the equation for , one obtains:
The sizes and depend only on the speed distribution within the "electron cloud". Since the drift speed is about 10 orders of magnitude smaller than the mean speed , the speed distribution does not change when an electric field is applied, and and and thus the whole expression for are constant.
history

Georg Simon Ohm was looking for a mathematical connection - a formula - to calculate the “effect of flowing electricity” (today's term: current intensity) depending on the material and the dimensions of a wire. He did not come across the law named after him by chance, but invested a lot of time and targeted work. The law he found in the form seems almost trivial to us: the greater the electrical voltage or the smaller the electrical resistance , the greater the current strength . These relationships can now be shown very easily with test devices that are available in every school with sufficiently low tolerances.
In 1825 such devices were not available to Ohm. Volta columns , batteries made of Daniell elements and so-called trough batteries (that is, several Daniell elements connected in series) in various designs served as voltage sources at that time . The voltage and current measurement devices that time were for Ohms lofty goal rather not suitable as sufficiently accurate measuring devices to obtain accurate readings in order to develop a formula as proof devices.
Ohm's experimentally innovative achievements consisted of having cleverly combined device components that had already been developed and the discoveries of several contemporary researchers. He then mathematically analyzed the measurement data obtained from this and interpreted their physical relationship.
First Ohm published an article in the Annalen der Physik und Chemie in 1825 , in which he described a measuring device he had developed, with which he came to more precise measurements than other researchers before him. On the one hand, Ohm used the magnetic effect of the electric current described by Hans Christian Ørsted in 1820 and, on the other hand, a very sensitive device for measuring force : he replaced the test specimen in the measuring device of the Coulomb rotary balance with a small bar magnet , placed this rotary balance on a wire carrying current and measured the force effect of the current on the magnet. He carried out this measurement with different wires and then looked for a mathematical relationship between wires and forces.
However , the measurement results published in the article Preliminary notification of the law according to which metals conduct contactelectricity in 1825 could not lead to a generally applicable formula because - analyzed in today's terms - the electrical power of all voltage sources used at that time (among other things due to the varying formation of gas bubbles on the Metal plates) fluctuates greatly. Ohm described this effect several times: The “effect on the needle” changes during the individual measurements and is also dependent, among other things, on the sequence of measurements taken. Nevertheless, in the published article, he ultimately derived a formula from his measured values that approximately reproduced the stated measured values.
Ohm's publication in the Annalen der Physik und Chemie was supplemented by a footnote by the editor of the journal. It refers to the discovery of the thermocouple by Thomas Johann Seebeck , about which a report written by Ørsted was published in the Annalen in 1823 and which helped Ohm achieve his experimental breakthrough.
In determining the law according to which metals conduct contact electricity, Ohm first critically described the “constant surge of force” in his previous experiments in 1826. This is followed by a description of a “rotary balance” that he designed and had a craftsman make (see illustration). The bow-shaped component is a thermocouple made of a bismuth bow , each of which has a copper strip attached to its legs . One leg was heated with boiling water, the other cooled with ice water . (The vessels for the temperature baths are not shown.) Ohm carried out his experiments in January 1826.
The reproducible temperature difference of approx. 100 ° C between the legs of the bracket creates a reproducible “exciting force” that does not “undulate” in an uncontrolled manner because no chemical reactions take place here. According to today's definitions, this “exciting force” corresponds to an open circuit voltage of approx. 7.9 mV.
Ohm measured the forces acting on the magnetic needle, when the ends of wires of different lengths in the with mercury -filled "egg cup" and appeared. From the measurement data obtained in this way, he developed the formula . Here stands for the electric current, for the "exciting force", stands for the line resistance of the rotary balance (including voltage source) and for the resistance length of the wires used. In another article in the same year, Ohm used the term “electrical voltage” instead of “exciting force”.
With the help of the thermocouple, Ohm was able to develop exactly the equation that we still use today to describe the relationships in a circuit:
- ( : Internal resistance of the voltage source; : external resistance connected to the voltage source components)
In 1827 Ohm published the book The galvanic chain, mathematically processed . On the first pages of this publication he postulated that electrical current behaves analogously to heat conduction in solid bodies (see Fourier's law ). Arguing geometrically, he first derived the dependencies of the current on the conductor length, the conductor cross-section and the material of different conductors, as evidenced by his measurements from 1826. In doing so, he now took into account all the components of a circuit, including those conductors that make up the thermocouple of his rotary balance, and thus summarized the internal and external resistances of a circuit to size . In doing so, he gave his discovery the mathematical structure that we know today as Ohm's law :
- ( "Magnitude of the current" Today , "the sum of all tensions," today ; : indoor + outdoor resistors, today ), so
In the following text, Ohm also conclusively derived the connections between series and parallel connection of conductors - i.e. resistors.
In his publications of 1826/27 Ohm - at that time "only" a teacher of physics and mathematics - explained the observations of many recognized scientists differently than they had done: They supported their observations and considerations by formulating models and theories for conducting electricity . Ohm, however, relied on his measurement results and on geometric considerations. This may be the reason why the importance of his work was not immediately accepted by the scientific community: “It was only in the course of the 1930s that his law was hesitantly recognized in Germany; internationally it was only noticed after a rediscovery in 1837. "
literature
- Georg Simon Ohm: The galvanic chain. Berlin, 1827 ( digitized and full text in the German text archive ).
Web links
Individual evidence
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: Internationales Electrotechnical Dictionary - IEV. Entry 131-12-04
- ↑ EN 80000-6, Quantities and Units - Part 6: Electromagnetism , 2008; Entry 6-46
- ^ DKE-IEV dictionary entry 131–12–02, footnote N4.
- ↑ Georg Simon Ohm: Preliminary announcement of the law according to which metals conduct contact electricity and later addendum . In: JC Poggendorff (Ed.) Annalen der Physik und Chemie. Berlin 1825, Volume 80, pp. 79-88. ( PDF )
- ^ Probably the first article on Hans Christian Ørsted's discovery in German: Ludwig Wilhelm Gilbert: An electrisch-magnetic experiment by Prof. Oersted. In: LW Gilbert (Ed.): Annals of Physics and Chemistry. Leipzig 1823, Volume 73, p. 278. ( PDF )
- ↑ Georg Simon Ohm: Preliminary announcement of the law according to which metals conduct contact electricity and later addendum . In: JC Poggendorff (Ed.) Annalen der Physik und Chemie. Berlin 1825, Volume 80, pp. 79-88 (especially pp. 83 and 87, respectively).
- ↑ Georg Simon Ohm: Preliminary announcement of the law according to which metals conduct contact electricity and later addendum . In: JC Poggendorff (Ed.) Annalen der Physik und Chemie. Berlin 1825, Volume 80, pp. 79-88 (especially p. 84).
- ↑ Georg Simon Ohm: Preliminary announcement of the law according to which metals conduct contact electricity and later addendum . In: JC Poggendorff (Ed.) Annalen der Physik und Chemie. Berlin 1825, Volume 80, pp. 79-88 (especially p. 83, footnote).
- ↑ Ludwig Wilhelm Gilbert: Note from Mr. Seebeck's new electro-magnetic experiments in Berlin, communicated by Mr. Oersted. In: LW Gilbert (Ed.): Annals of Physics and Chemistry. Leipzig 1823, Volume 73, pp. 430-432. ( PDF )
- ↑ Georg Simon Ohm: Determination of the law according to which metals conduct contact electricity, together with a draft for the theory of the voltaic apparatus and the Schweigger multiplier. In: JSC Schweigger (ed.): Journal for chemistry and physics. Halle 1826, Volume 46, pp. 137–166. ( PDF )
- ↑ Georg Simon Ohm: Determination of the law according to which metals conduct contact electricity, together with a draft for the theory of the voltaic apparatus and the Schweigger multiplier. In: JSC Schweigger (ed.): Journal for chemistry and physics. Halle 1826, Volume 46, pp. 137–166 (especially p. 139).
- ↑ Georg Simon Ohm: Determination of the law according to which metals conduct contact electricity, together with a draft for the theory of the voltaic apparatus and the Schweigger multiplier. In: JSC Schweigger (ed.): Journal for chemistry and physics. Halle 1826, Volume 46, pp. 137–166 (especially pp. 144–149).
- ↑ Georg Simon Ohm: Determination of the law according to which metals conduct contact electricity, together with a draft for the theory of the voltaic apparatus and the Schweigger multiplier. In: JSC Schweigger (ed.): Journal for chemistry and physics. Halle 1826, Volume 46, pp. 137–166 (especially panel 3, Figure 1). ( PDF )
- ↑ Georg Simon Ohm: Determination of the law according to which metals conduct contact electricity, together with a draft for the theory of the voltaic apparatus and the Schweigger multiplier. In: JSC Schweigger (ed.): Journal for chemistry and physics. Halle 1826, Volume 46, pp. 137–166 (especially p. 151).
- ↑ Georg Simon Ohms laboratory book from 1825/26. Special collection of the Deutsches Museum in Munich.
- ↑ Georg Simon Ohm: Attempt of a theory of the electroscopic phenomena produced by galvanic forces. In: JC Poggendorff (Ed.): Annals of Physics and Chemistry. Berlin 1826, Volume 82, pp. 459-469 (especially p. 459). ( PDF )
- ↑ Georg Simon Ohm: The galvanic chain, processed mathematically. Berlin: Riemann 1827. Digitized and full text in the German Text Archive ; Digitized as PDF ; [Reprint of the edition, [Riemann], 1827] Saarbrücken 2006, ISBN 3-939962-03-1 .
- ↑ Georg Simon Ohm: The galvanic chain, processed mathematically. Berlin: Riemann 1827, p. 36.
- ↑ Jörg Meya u. a .: The fifth element. Effects and interpretations of electricity. Reinbek near Hamburg 1987, ISBN 3-499-17726-9 , p. 194.
















































