Voltage source
In circuit theory in electrical engineering, a voltage source is an active two- terminal network that supplies an electrical voltage between its connection points . As an essential property, this voltage depends only slightly or - in the model of the ideal voltage source within the framework of the network analysis - not at all on the electrical current that is drawn from the source. The supplied electrical voltage is ideally independent of the connected consumer. If the voltage source realizes the model behavior within only small deviations, it is also referred to as a constant voltage source or, if it is particularly precise, as a reference voltage source .
A voltage source is preferably used as an electrical energy source that supplies electrical power depending on the connected consumer, but must not be confused with a power source (see below ). It also occurs as a supplier of electrical signals .
A voltage source can also be an object that can only generate an electric field , but is only capable of delivering current for a short time or to an unusable extent.
context
The counterpart to the voltage source in the context of electrical network analysis is the two-pole power source , which supplies a certain electrical current - regardless of the voltage applied to its terminals. Any arrangement of linear voltage and current sources and resistors in the form of an electrical circuit can always be fully described to the outside as a two-pole by only one voltage source with an internal resistance . This relationship is also referred to as the Thévenin theorem and plays a role in electrical circuit analysis , as it allows complicated circuits to be reduced to simplified equivalent circuits , which are then more easily accessible for analysis.
In the equivalent circuits, the voltage source is always viewed as independent of the current strength. In reality, this behavior can only be achieved approximately; then further components have to be inserted in the equivalent circuit diagram to better describe the reality . In the simplest case, an ohmic internal resistance in series with the voltage source is used for this . In the case of technically used voltage sources, attempts are usually made to keep the internal resistance as low as possible.
Types of voltage sources
DC and AC voltage sources
DC voltage sources keep their voltage value constant over time. Such sources that work as energy sources are e.g. B. Batteries , accumulators and power supplies . There are also voltage sources that are not very resilient, but are important as signal sources or measuring sensors , e.g. B. Thermocouples .
Accordingly, an AC voltage source generates a voltage that changes periodically over time. These sources include B. Generators , transformers , signal generators and also power supplies . The electrical power supply network also represents an alternating voltage source. Furthermore, there are also sources that can hardly be loaded, for example for the transmission of messages or for the transmission of measurement and sound signals , e.g. B. Microphones .
Asymmetrical, bipolar and symmetrical power supplies
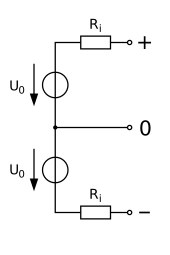
If a DC voltage source has two connections, one of which is declared to be the general reference or ground potential, one speaks of an asymmetrical voltage source.
In the case of a bipolar DC voltage supply, a positive and negative voltage, based on a common ground potential, z. B. +15 V and −10 V are provided. If the amount of the positive and negative voltage is also the same, it is a symmetrical DC voltage supply . Such a voltage supply is often required for assemblies that process AC voltages, for example audio amplifiers .
Controlled and regulated voltage sources
In addition to the independent voltage source with a fixed source voltage, there is the controlled voltage source , the source voltage of which is a function of an external voltage or current that is connected to separate connection points.
Instead of such an external manipulated variable, the regulated voltage source is routed through a control loop in such a way that the output voltage adjusts to a predetermined setpoint . This compensates for interference caused by changes in the current load, fluctuations in the mains voltage or temperature drift. With some laboratory power supplies , the voltage at the consumer input (instead of the source output) can also be regulated, which also regulates the influences of the lines and contacts. It is irrelevant whether the regulated voltage source is a direct or alternating voltage source.
Technical descriptions
Basics
The following terms are used in this article:
- Output or terminal voltage
- Source voltage , formerly also known as primary voltage or electromotive force (EMF)
- This is the maximum voltage that the source can deliver. It occurs when the terminals are open (open circuit).
- This is the maximum current that the source can deliver. It occurs when the terminals are connected to one another without resistance (short circuit).
- Internal resistance , also called source resistance referred
- Consumer resistance , also known as load resistance or input resistance called a sequential circuit
The following counting direction is also used:
In the case of a passive component or consumer, the reference direction of the current intensity should relate to the polarity of the voltage. A consumer counter arrow system as in the following equivalent circuit ensures that voltage and current have the same sign. A positive voltage from a to b generates a positive current from a to b in the consumer . (If one of the two arrows is reversed, a minus sign would have to be inserted into Ohm's law.) Through the consistent use of the signs in the entire circuit, the current flows against the voltage inside the voltage source.
Ideal and real voltage sources
An ideal voltage source is a source that always delivers the same voltage regardless of the downstream consumer. Terminal and source voltage are therefore identical; the source of energy is assumed to be infinite. Since this is strictly impossible to achieve in practice, equivalent circuits for real voltage sources are mostly used in technical calculations . The linear voltage source consisting of a series connection of an ideal voltage source and an ohmic internal resistance has proven itself, because it describes many phenomena with satisfactory accuracy. With this extended model, the influence of downstream loads on the actually applied terminal voltage of the source can be reproduced during calculations. The more the source is loaded by the consumer, the lower the voltage applied to the terminals drops. The internal resistance limits the maximum current strength that is possible in the event of a short circuit ( ). The short-circuit current strength is then calculated
The lower the internal resistance of the source, the greater the maximum current strength. In practice, the internal resistance of a voltage source can change with the load and with time; for example, the internal resistance of a new battery is much lower than that of a used one.
In the case of voltage sources that function as an energy source, the aim is to keep their internal resistance as small as possible, at least much smaller than that of the consumer. On the other hand, there is the risk of a destructive overcurrent in the event of a short circuit , which is why the overcurrent must be switched off quickly by fuses . With electronic voltage sources, in contrast to the ideal voltage source model, the current that can be delivered is limited. If the current exceeds a certain limit, the voltage can collapse.
In the case of voltage sources that function as signal sources that can only generate limited power, different aspects apply, see below in the Power section .
Characteristics
The terminal voltage of a voltage source with the source voltage as a function of the current strength drawn can be graphically represented as a characteristic curve .
- With an ideal voltage source, this is a horizontal straight line according to the definition. It is shown opposite as a red line.
- A real voltage source with an internal resistance provides a falling characteristic curve in which the voltage decreases with increasing current strength. The following applies to the equivalent circuit diagram shown above:
-
- .
- In the case of a linear source with an ohmic internal resistance, this results in an inclined straight line. Two characteristic curves with different internal resistance are shown in turquoise for this purpose. They achieve with the applicable short-circuit current strength .
- A non-linear source has a curved characteristic. An example of such a source is the solar cell . Their behavior is shown in green. This source can only be viewed as a voltage source in the flat area of its characteristic curve; in the steep area when the short circuit is approached, its behavior is more appropriately described by a current source . Each individual case of non-linearity requires a special equivalent circuit, so that no details can be dealt with here.
Parallel and series connection of voltage sources
Series connection
If more voltage is required by the consumer than a single source can supply, the series connection of several potential-free voltage sources results in a total voltage from the sum of the voltages of the individual voltage sources. The total swell resistance is also equal to the sum of the individual internal resistances. The current is identical for all sources in terms of magnitude and sign or in frequency , phase angle and peak value .
Parallel connection
If more current is required by the consumer than a single source can supply, so that a parallel connection of voltage sources is necessary, this is only possible to a limited extent and only with real sources. If necessary, source resistances must be simulated using external resistors connected to the lines. These must be so large that the voltage at the consumer is lower than the smallest of the no-load voltages due to their voltage losses. It is always important to ensure that all voltage sources connected in parallel
- can assume the same amount with regard to the terminal voltage,
- have the same sign ( polarity ) for direct voltage or the same phase angle for alternating voltage ,
- are potential-free or are grounded at the same pole; if there is more than one earth point, equalizing currents can flow (see hum loop ).
If these points are not observed, this leads to a mostly undesirable current between the sources. Depending on the current level or the design of the voltage sources, this can lead to the destruction of individual partial sources. These criteria can also be met with appropriate electronic protective circuits that monitor and regulate the voltages of the individual voltage sources.
The total voltage of several voltage sources connected in parallel depends on the source voltages and the internal resistances of the individual voltage sources, as described above. The total current is the sum of the currents of the individual sources. In order to calculate the internal resistance, the individual voltage sources must be transformed into current sources (see below ), the resistance can then be calculated from the parallel connection of the individual internal resistances.
power
With regard to the electrical power , a voltage source must be differentiated
- the power that can be generated by the source,
- the power generated in connection with a consumer,
- the power supplied to a consumer.
Most of the voltage sources occurring in practice behave like the linear source model when used as intended ; then the voltage adjustment applies regardless of the current strength or load. For this, the power that can be generated by the source must have significant reserves compared to the power actually generated.
According to the equivalent circuit diagram, the following applies to a real voltage source with the internal resistance together with a consumer resistance
- .
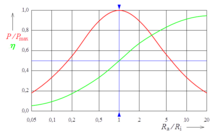
In the two borderline cases of consumer resistance, short circuit and interruption , no power is supplied to the consumer. In between, this power is greater than zero; thus the consumer receives a maximum of power at a certain resistance value between the borderline cases. This case is called power adjustment . It occurs when is. The maximum power supplied results from
- .
In the case of voltage sources for the energy supply, this is never called up, but only in the case of low-power sources such as e.g. B. Antennas. With sources operated in power adjustment, the consumer receives half of the power generated.
The power loss of the internal resistance
is almost completely converted into thermal output . She is partly responsible for the fact that z. B. Heat batteries when discharging and accumulators when charging. In the event of a short circuit, the heat energy converted at the internal resistance can damage the voltage source and objects in its vicinity through heat, destroy it or set it on fire.
The efficiency of a voltage source results from the ratio of the power supplied to the consumer to the power generated by the voltage source . With the real voltage source, part of the voltage generated is lost. With the same current strength in the entire current path, part of the power is correspondingly lost. for true
- .
For the highest possible efficiency , that is the state of the voltage adjustment. In the borderline case the ideal voltage source is .
Transformation voltage source ↔ current source
According to the Thévenin and Norton theorems, every linear voltage source can also be viewed as a linear current source. Which term is used depends on which ideal form the behavior of the source is viewed more closely. The following equations can be converted into each other, the left describes the voltage source, the right the current source.
literature
- Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretical electrical engineering . 18th edition. Springer, 2008, ISBN 978-3-540-78589-7 .
- as well as the specialist books listed in the individual references
Individual evidence
- ↑ IEC 60050, see DKE German Commission for Electrical, Electronic and Information Technologies in DIN and VDE: International Electrotechnical Dictionary IEV entry 131-12-21.
- ↑ DIN EN 60375: 2004-04, No. 8.1.1
- ^ Wilfried Weißgerber: Electrical engineering for engineers, Volume 1 .
- ^ Heinrich Frohne , Karl-Heinz Locher, Hans Müller: Moeller Fundamentals of Electrical Engineering .
- ↑ Ulrich Tietze and Christoph Schenk: Semiconductor circuit technology .
- ^ Ralf Kories and Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik .
- ^ Rainer Ose: Electrical engineering for engineers, Volume 1 .
- ↑ DIN EN 60375, No. 6.1