Effective resistance

Alternating current resistance as a pointer in the complex plane with active resistance  and reactance  for sinusoidal currents and voltages ${\displaystyle {\underline {Z}}}$ ${\displaystyle R}$ ${\displaystyle X}$

In electrical engineering , electrical resistance is a measure of the electrical voltage required to allow a specific electrical current to flow through an electrical conductor. If the resistance of a consumer behaves like an ohmic resistance in terms of effective values , but behaves differently with alternating current than with direct current , the resistance is described by two components, the effective resistance and the reactance . The effective resistance does not allow a time delay between current and voltage and therefore does not produce a phase shift between current and voltage in the case of sinusoidal current . It can be frequency dependent or independent, depending on the circumstances; see under keyword electrical resistance .

The effective resistance also stands for the part of the consumer who irreversibly converts electrical energy into another form of energy (e.g. mechanical, thermal or chemical energy). In contrast, the reactance stands for the part of the consumer that allows energy to commute between producer and consumer.

The effective resistance is also known as resistance .

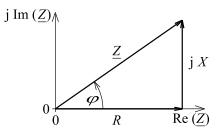
In the complex AC calculation , the effective resistance denotes the real part of the complex resistance  . ${\displaystyle R}$ ${\displaystyle {\underline {Z}}}$

${\displaystyle R=\operatorname {Re} \ {\underline {Z}}}$

${\displaystyle R=Z\cos \varphi ={\frac {U}{I}}\cos \varphi }$

See also

• Admittance (complex representation of the conductance)
• Impedance (complex representation of resistance)
• Active power , reactive power
• Active current

Web links

Wiktionary: Resistance  - explanations of meanings, word origins, synonyms, translations