Electrical capacitance
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Electrical capacitance | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
The electrical capacity (symbol , from Latin capacitas 'capacity' ; adjective capacitive ) is a physical quantity from the field of electrostatics , electronics and electrical engineering.
The electrical capacitance between two electrically conductive bodies isolated from each other is equal to the ratio of the amount of charge stored on these conductors ( on one and on the other) and the electrical voltage between them :
It is determined by the dielectric constant of the insulating medium and the geometry of the body, including the distance. As a result (provided the capacity is constant) and are in a proportional relationship to each other.
In the case of accumulators and batteries , the term “ capacity ” is used for the maximum amount of charge that can be stored in them. It is given in ampere hours (Ah). However, this capacity of the electrical charge has nothing to do with the electrical capacity ( Farad ) shown here, nor with the power capacity ( watt ).
Capacity of a capacitor
A technical application is the capacity in the form of electrical capacitors , which are characterized by the specification of a certain capacity. The term "capacity" is used colloquially as a synonym for the electrical component capacitor itself ( english capacitor used).
Capacitors represent a conductor arrangement with two electrodes for the separate storage of electrical charge and . From a physical point of view, the electrical flow comes from the separate electrical charges and , which are transported from the external voltage source with the voltage to the electrodes, whereby:
results. This connection is formally established using Gauss law . The electrical capacity of a capacitor can then be expressed as the ratio of the amount of charge to the voltage applied :
- .
This is usually a constant parameter that results as follows.
A body to which a positive electrical charge is placed has an electrical field that counteracts the movement of a further positive electrical charge on the body. But if there is a negatively charged body nearby, the repelling electric field of the positive body is weakened (the positive charge to be moved towards the body also feels the force of the attractive negative charge). This means that less voltage is required to move the further positive charge onto the already positively charged body than without the second negatively charged body. So the first body has a higher capacity. The same applies of course to the second body. The weakening of the electric field through one charged body on the other charged body is influenced by their geometry and the permittivity of the insulating medium between the two bodies.
In a simplified analogy, the capacity corresponds to the volume of a compressed air tank with a constant temperature. The air pressure is analogous to the voltage and the amount of air is analogous to the amount of charge . Therefore, the amount of charge in the capacitor is proportional to the voltage.
This law also applies to the so-called pseudocapacitance , a voltage-dependent electrochemical or Faraday storage of electrical energy within narrow limits , which is associated with a redox reaction and with a charge exchange on the electrodes of supercapacitors , although in contrast to accumulators there is no chemical change on the electrodes entry.
Among other things, the Physikalisch-Technische Bundesanstalt (PTB) deals with capacity standards .
unit
The electrical capacitance is measured in the derived SI unit Farad . A farad (1 F) is the capacity that stores a charge of 1 coulomb (1 C = 1 As) when a voltage of 1 volt is applied :
A capacitor of capacitance 1 Farad charges at a constant charging current of 1 Ampere in 1 tick to the voltage 1 volt on. The SI unit Farad, named in honor of the English physicist and chemist Michael Faraday , has now established itself internationally everywhere.
Obsolete unit
Until the middle of the 20th century, the capacitance of capacitors was often labeled with the unit of capacitance cm . This specification in centimeters comes from the fact that the capacity in the Gaussian system of units , which is practically hardly used today , is expressed in the length dimension. For example, a metal ball with a radius of 5 cm has a capacitance of 5 cm compared to an infinite counter-electrode.
The illustration opposite shows a paper capacitor made by SATOR from the former company Kremenezky , Mayer & Co from 1950 with a capacity of 5000 cm. This corresponds to the capacity of a metal ball with a radius of 5000 cm. Represented in today's common SI system of units , this is approximately 5.6 nF.
A capacity of 1 cm in the Gaussian system of units corresponds to approx. 1.1 pF in the SI system of units, the conversion factor is 4 π ε 0 . This conversion comes about through the definition of the field constant in the Gaussian system of units :
- in the Gaussian system of units ( not in the International System of Units (SI) )
Capacity of certain conductor arrangements
There are analytical solutions or convergent series developments for the capacity of a series of simple ladder arrangements. The following table shows some examples:
| designation | capacity | Schematic representation |
|---|---|---|
| Plate capacitor |

|
|
|
Coaxial cable or cylinder capacitor |

|
|
| Spherical capacitor |
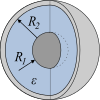
|
|
|
Ball , counter electrode with towards infinity |
||
| Parallel cylinders ( Lecher line ) |

|
|
| A ladder parallel over a flat surface. |
 |
|
| Two spheres with the same radius |
|
 : Spacing of the balls, : : Euler-Mascheroni constant |
| Disc towards infinity |
 : Radius |
|
| Straight piece of wire (long cylinder) towards infinity |
: Length : Wire radius : |
Here, A denotes the area of the electrodes, d their distance, l their length, as well as their radii and the permittivity (dielectric conductivity) of the dielectric. The following applies , where stands for the electric field constant and for the relative permittivity. In the schematic representation, the conductors are colored light gray or dark gray and the dielectric is colored blue.
Capacity calculations
The following general equations for determining the capacitance apply to the time-dependent quantities current , voltage and charge at a constant electrical capacitance :
An expression for the capacity of any electrode arrangement or charge distribution can be derived using Gauss's theorem :
The dielectric shift is:
For a vacuum this equation simplifies to:
A calculation of the capacitance requires knowledge of the electric field. For this, the Laplace equation has to be solved with a constant potential on the conductor surfaces. In more complicated cases there is no closed form of the solution.
Measure capacity
Measuring the capacitance is not only used to check the capacitance of a capacitor (component), but is also used, for example, in capacitive distance sensors to determine the distance. Other sensors (pressure, humidity, gases) are often based on a capacitance measurement.
According to the above-mentioned relationships, the capacity can be determined as follows:
- Charge with constant current and observe the rate of voltage rise
- Measuring the resonance frequency of an LC resonant circuit formed with the capacitance
- Applying an alternating voltage and measuring the current flow
The last-mentioned method in particular is used in capacitance measuring devices, whereby not only the magnitude of the current, but also its phase relation to the voltage is recorded. In this way, the impedance and the loss angle or the quality factor of the capacitor can also be determined.
literature
- Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretical electrical engineering . 18th edition. Springer, 2008, ISBN 978-3-540-78589-7 .
References and comments
- ^ JC Maxwell: A Treatise on Electricity and Magnetism . Dover, 1873, ISBN 0-486-60637-6 , p. 266 ff.
- ^ AD Rawlins: Note on the Capacitance of Two Closely Separated Spheres . In: IMA Journal of Applied Mathematics . 34, No. 1, 1985, pp. 119-120. doi : 10.1093 / imamat / 34.1.119 .
- ^ JD Jackson: Classical Electrodynamics . Wiley, 1975, p. 128, problem 3.3.
- ^ JC Maxwell: On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness . In: Proc. London Math. Soc. . IX, 1878, pp. 94-101. doi : 10.1112 / plms / s1-9.1.94 .
- ↑ LA Vainshtein: Static boundary problems for a hollow cylinder of finite length. III Approximate formulas . In: Zh. Tekh. Fiz. . 32, 1962, pp. 1165-1173.
- ↑ JD Jackson: Charge density on thin straight wire, revisited . In: Am. J. Phys . 68, No. 9, 2000, pp. 789-799. bibcode : 2000AmJPh..68..789J . doi : 10.1119 / 1.1302908 .








![[C] = \ frac {[Q]} {[U]} = \ frac {1 \, \ mathrm {C}} {1 \, \ mathrm {V}} = \ frac {1 \, \ mathrm {As }} {1 \, \ mathrm {V}} = 1 \, \ mathrm {F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cfe58eeb914791a0546e3cf20f16ce90a579d18)




















![{\ displaystyle C = {\ frac {2 \ pi \ varepsilon l} {\ Lambda}} \ left \ {1 + {\ frac {1} {\ Lambda}} \ left (1- \ ln 2 \ right) + {\ frac {1} {\ Lambda ^ {2}}} \ left [1+ \ left (1- \ ln 2 \ right) ^ {2} - {\ frac {\ pi ^ {2}} {12} } \ right] + {\ mathcal {O}} \ left ({\ frac {1} {\ Lambda ^ {3}}} \ right) \ right \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a151e31bc5ed0ff3aa5d9079fe5e89c8a7aa8acc)




















