Skin effect
The skin effect (from English skin for skin) is a current displacement effect in electrical conductors through which higher-frequency alternating current flows , through which the current density inside a conductor is lower than in the outer areas. The cause of the skin effect is that the alternating fields penetrating the conductor are largely attenuated due to the high conductivity of the material before they even reach the inside of the conductor.
The skin effect occurs in thick conductors relative to the skin depth and also in electrically conductive shields and cable shields . With increasing frequency, the skin effect favors the transfer impedance of shielded cables and the shielding attenuation of conductive shields, but increases the resistance of an electrical cable .
A similar related effect of neighboring electrical conductors is what is known as the proximity effect .
root cause
The skin effect occurs in a conductor of limited conductivity in the presence of an electromagnetic alternating field .
When energy is transmitted via an electrical conductor with alternating current , part of the electromagnetic wave and thus of the electromagnetic energy penetrates along the conductor. This fact binds the wave to the conductor.
The penetration of the field is the cause of a current flow in the conductor. Using the example of a metallic wire through which a direct current flows, this can easily be justified with the help of Ohm's law . This states that the current density in the conductor is proportional to the (current-driving) electric field strength. Without an electric field, no current flow occurs in a metallic wire. Since every current is surrounded by a magnetic field according to Ampère's law, magnetic fields penetrate the conductor along with the electric current.
According to the law of induction , the change in the field leads to the formation of electrical vortex fields in the conductor.
- The penetrating alternating fields are weakened because they induce fields opposite to them. See Lenz's rule
- Since they cause eddy currents in the resistive conductor, field energy is converted into heat. See eddy current brake
- In contrast to the speed of light in a vacuum, the spread of the fields is greatly slowed down. See shortening factor
calculation
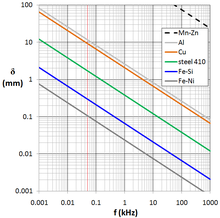
Frequency-dependent penetration depth (drop to 1 / e , approx. 37%) in a copper line frequency Penetration depth frequency Penetration depth 5 Hz 29.7 mm 5 MHz 29.7 µm 16 Hz 16.6 mm 16 MHz 16.6 µm 50 Hz 9.38 mm 50 MHz 9.38 µm 160 Hz 5.24 mm 160 MHz 5.24 µm 500 Hz 2.97 mm 500 MHz 2.97 µm 1.6 kHz 1.66 mm 1.6 GHz 1.66 µm 5 kHz 938 µm 5 GHz 938 nm 16 kHz 524 µm 16 GHz 524 nm 50 kHz 297 µm 50 GHz 297 nm 160 kHz 166 µm 160 GHz 166 nm 500 kHz 93.8 µm 500 GHz 93.8 nm 1.6 MHz 52.4 µm 1.6 THz 52.4 nm
To describe the skin effect, a diffusion equation can be formulated using Maxwell's equations , the finite conductivity of the conductor and Ohm's law , which describes the penetration of the fields into a conductor.
The solutions depend in detail on the exact geometric arrangement (e.g. shape of the conductor) and the exact excitation (field distribution in the outside area). As a model, it should be assumed for the following considerations that in the half-space (outside the conductor) a harmonic distribution of the E-field independent of the x and y coordinates with a pure component is given.
The associated H-field has a pure component
The considered propagation takes place in the half-space , which is penetrated by a homogeneous conductive material with the specific conductivity . denotes the real part of a complex number and the imaginary unit .
The solutions show that the fields can only penetrate the conductor from the outside very slowly. The phase velocity of the penetrating damped “wave” can be calculated using the equation, assuming that the phase currents in the conductor are much greater than the displacement currents
- With
be calculated. For a copper conductor with the specific conductivity , the magnetic field constant, this results in a phase velocity of at a frequency of , which is a very low value compared to the speed of light in a vacuum .
The decisive factor for the skin effect is that the penetrating field is dampened to a greater or lesser extent, depending on the frequency, due to the eddy currents associated with the propagation in the conductor. The current density decreases exponentially at a distance from the edge according to the following equation :
where denotes the current density at the edge and the equivalent conductive layer thickness. In practice, these equations are also used for approximate calculations for radially symmetrical conductors.
In many cases, the thickness of the conductive layer for good electrical conductors can be approximated using the following equation:
With
- the resistivity of the conductor. This is the reciprocal of the electrical conductivity of the material:
- - angular frequency
- - absolute permeability of the conductor, which is the product of the permeability constant and the relative permeability number of the conductor.
This dimension describes the wall thickness of a fictitious round conductor, which has the same resistance for direct current as a full conductor due to the skin effect for the circular frequency . The approximation given applies to a round conductor whose radius is very small compared to the length, but significantly larger than δ. In this case, δ indicates the depth at which the current density has dropped to the 1 / e part of the value of the edge.
For direct current with aspires . The field can therefore penetrate the entire conductor. This means that the skin effect is only noticeable with alternating current and, depending on the frequency and conductor material, leads to a different depth of penetration into the conductor (see table).
The penetration depth decreases with increasing permeability (magnetism) and increases with increasing electrical resistance . The fact that the penetration depth decreases with increasing permeability , for example, means that iron with its relatively high magnetic conductivity (µ r > 1000) is unsuitable as a high-frequency conductor.
At the level of electrical circuits, the weakening of the E-field becomes noticeable as a reduction in the effective conductor cross-section, so that the impedance ( impedance ) of the conductor increases. The higher the frequency , the stronger this effect is until, at high frequencies, only a thin area on the surface carries most of the current.
A good approximation of the ratio between the effective resistance of the conductor R to the DC resistance R DC is
with .
It also applies to large penetration depths, but is not entirely continuous around x = 1.
The following equation represents a more precise form for the equivalent conductive layer thickness, which is used in particular for poor electrical conductors and non-metals and which takes the influence of permittivity into account:
This equation can be used as an approximation up to frequencies well below the plasma oscillation of the material. If the angular frequency is significantly smaller than , the additional factor with the permittivity is omitted and the above simple equation results. For good electrical conductors such as copper, the equivalent conductive layer thickness can be expressed up to frequencies around 1 EHz (10 18 Hz) without considering the permittivity . In bad electrical conductors, on the other hand, the right factor increases; at frequencies that are significantly higher , the equivalent conductive layer thickness no longer decreases, but approaches an asymptotic value that no longer depends on the frequency:
An example of a material for a poor electrical conductor is undoped silicon , which has an equivalent conductive layer thickness of around 40 m due to its intrinsic conductivity at 100 Hz. If the frequency is increased to a few MHz and above, the equivalent thickness of the conductive layer does not drop below 11 m. Due to the high values of the equivalent conductive layer thickness in the range of a few meters compared with good conductors, the frequency-dependent component of the skin effect does not need to be taken into account with these materials. The example is important for inductive heating for zone melting of silicon.
Depending on the ratio of the penetration depth to the mean free path of the charge carriers, a distinction is made between the following cases:
- normal skin effect and
- abnormal skin effect.
The anomalous skin effect is used to measure the Fermi areas of materials. This requires low temperatures (≈ 1 K) and pure materials so that the mean free path is large.
Derivation
The Maxwell equations in the neutral electrical conductor are for complex harmonic fields
- ,
where k denotes the wavenumber vector and ω the angular frequency, as follows
- ,
- ,
- ,
- .
For the sake of simplicity, excluding permeability and permittivity, it was assumed that the influence of conductivity σ is dominant in the medium. Especially for magnetic conductors (e.g. iron) the derivation would have to be modified accordingly. The imaginary unit i occurs because of the spatial as well as temporal derivatives of the harmonic approach that occurs in the Maxwell equations. The harmonic approach is justified because the harmonic fields represent a basis of the solution space of the Maxwell equations in the ladder, so every concrete solution can be put together from them by superposition.
In the last equation - Ampere's law - the last term on the right-hand side represents the displacement current in its form for complex fields, the penultimate term with the conductivity σ, on the other hand, represents the current component according to Ohm's law. Finally, the third equation represents the induction law for harmonic fields. The first two equations (Gauss law in the neutral medium and the absence of sources of the magnetic field) only state for harmonic fields that electric and magnetic fields are perpendicular to the direction of propagation k. From the appearance of the vector product in the law of induction it also follows that the electric and magnetic fields are perpendicular to each other. All in all, E, B and k form an orthogonal tripod.
By forming the vector product of the wave number vector k on both sides with the law of induction, the equation is obtained after reducing the imaginary unit
- .
If you insert Ampere's law on the right side and use the orthogonality of E and k on the left side, you finally get
- .
or.
- .
Since E is a spatially and temporally variable function, this equation can generally only be fulfilled everywhere and for all time if the term in brackets, which is made up of constants, is zero. This is the dispersion relation in the ladder:
- .
The formal solution for the spatial magnitude of the wavenumber vector reads accordingly
- .
By extracting the angular frequency and the speed of light from the root it can be further transformed,
- ,
where the expression for the vacuum speed of light
- .
was used. For small frequencies ω (which for real conductors can still be extremely high compared to the usual frequencies in circuits, see also the reference to the plasma frequency in the last section) the imaginary summand under the root is large compared to 1 and results in the dispersion relation the following approximation:
- .
If you question the origin of the neglected term, you can see that it corresponds exactly to the displacement current in Amper's law (in Maxwell's form). The skin effect can therefore be explained solely by means of magnetic induction and (pre-Maxwellian) quasi-static magnetic field generation.
Because of
- .
finally follows
- .
As you can see, the wavenumber receives not only its real part, which corresponds exactly to the free wave propagation in a vacuum, but also an imaginary part. Its meaning can be understood if one assumes a wave propagation in the x-direction and uses the wave number in the harmonic approach made at the beginning. Then results for the electric field, for example
- ,
with the formal plane wave
- .
The field propagation in the conductor takes place in such a way that a plane wave is damped in the direction of propagation with an exponential factor. Damping to the portion 1 / e of the output field strength occurs after a distance x = δ, for
is. This then finally results in the depth of penetration under the assumptions made as
- .
The validity of these considerations is not limited to plane wave solutions, since all forms of propagation in the conductor can be composed (superposed) of these solutions and thus also contain the exponential attenuation with the penetration depth in an implicit form. When designing solutions for a special geometry, however, the task arises to link the interior of the conductor to the exterior via the boundary conditions. This would be e.g. B. also necessary for the cylindrical conductor geometry, if one wanted to calculate the concrete damping profile over the cross-section. Due to the superposition of many damped plane waves with different directions of propagation, the resulting damping will no longer be an exact exponential curve (which is not even possible, since the path from the surface to the axis of the conductor is finite). This deviation from the exponential curve becomes more pronounced the closer the cross-sectional radius is to the penetration depth or the further it is below it (which is the rule for LF circuits). For radii that are much larger than the penetration depth, the exponential curve is given approximately with sufficient accuracy. The exponential attenuation applies precisely to waves that hit the flat surface of a conductor head-on. In any case, the penetration depth fulfills its property as a limit value for whether a conductor can still be considered a volume conductor in a certain frequency range or must already be considered a surface conductor.
Measures against the increase in the resistance layer
In order to keep the effects of the skin effect as small as possible, cables with the largest possible surface area are used in high-frequency technology , for example in the form of thin-walled hose pipes, strands or tapes. The low losses of waveguides are partly due to the fact that a large part of the inner surface is not significantly involved in the flow of current.
Furthermore, the surfaces of high-frequency or ultra-high frequency cables are often coated with precious metals such as silver or gold in order to reduce the specific resistance of the outer surface of the wire, which conducts by far the largest part of the current. In the case of gold in particular, the fact that this metal does not oxidize in air is used , so that the surface retains a long-term stable conductivity. Because gold itself has a lower electrical conductivity than copper, but a significantly better one than copper oxide.
Care is also taken to ensure that the conductor surface is very smooth, since rough surfaces represent a longer path for the current and therefore greater resistance. Ferromagnetic conductor materials are also particularly disadvantageous since the penetration depth is greatly reduced in these. For this reason, they are also often coated with metal.
HF cables and coil windings are often made of stranded or interwoven individual wires that are isolated from one another ( high-frequency stranded wire ). The strands are constructed as so-called Milliken conductors, in which the individual wires, isolated from one another, lie alternately inside and outside in the overall cross-section. As a result, the same current flows in each individual wire and the voltages induced between them cancel each other out.
High-voltage overhead lines are twisted conductors . The steel carrying cables are inside and the aluminum cables are outside. However, due to the low network frequency of 50–60 Hz, the skin effect only comes into play with large cross-sections. Due to the skin effect, the current flows primarily in the outer layer of aluminum. This line structure also has structural advantages: the steel core inside can absorb significantly greater forces than aluminum . The inside of the steel can also be better protected from the elements.
The constantly increasing operating frequencies of switched-mode power supplies also require the skin effect to be taken into account when designing their transformer windings . Therefore, HF litz wires or tapes are increasingly being used here as well.
About the term current displacement
An explanatory approach used in numerous introductory textbooks describes the skin effect as shown in the adjacent picture as a displacement of the current from the inside of the conductor to the outside. According to this, the “actual” current marked with causes eddy currents ( red circles marked with ) due to the flow law and induction law , which are opposite to the original current inside the conductor and are intended to increase the current flow at the edge of the conductor. The popular term “current displacement” is based on this idea.
However, the explanatory approach to “current displacement” fails to recognize that the physical process is mathematically described by a diffusion equation that describes the diffusion of the electromagnetic field (from outside to inside) into the conductor. The physical process is therefore in no way about a field displacement directed from the inside out.
Further weaknesses of this explanatory model are the fact that
- the explanatory approach does not describe any field spread
- the phase position between the drawn eddy currents and the “causative current” marked with is not taken into account
- the eddy currents are justified exclusively on the basis of the "causal" current, although all currents (including the eddy currents) are included in the law of flow
- the explanatory approach does not provide any explanation as to why the penetration depth is largely independent of the conductor diameter and the magnitude of the current
Against this background, the explanatory approach appears to be neither qualitatively nor quantitatively suitable for describing the skin effect.
Web links
Individual evidence
- ^ JD Jackson: Classical Electrodynamics. 2nd edition, Chap. 7.7: "The waves given by (7.80) show an exponential damping with distance. This means that an electromagnetic wave entering a conductor is damped to 1 / e = 0.369 of its initial amplitude in a distance the last form being the approximation for good conductors . The distance is called the skin depth or penetration depth. […] This rapid attenuation of waves means that in high frequency circuits current flows only on the surface of the conductors.
- ↑ To justify this, imagine a current thread flowing in the middle of the conductor in the longitudinal direction of the conductor. This is surrounded by a magnetic field both inside and outside the conductor.
- ↑ Calculated for a specific resistance of copper wire of 0.0174 Ω · mm² / m
- ↑ Heino Henke: Electromagnetic fields: theory and application, chap. 12.7
- ↑ The term “wave” is placed in quotation marks because there is no wave in the narrower sense (i.e. a solution to a wave equation). However, the term is useful in describing the process of the invading field clearly. For a discussion of this see also thermal wave
- ↑ U. van Rienen: The skin effect . In: Lecture documents University of Rostock . ( Download (PDF; 3400 kB)).
- ^ Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Fundamentals of theoretical electrical engineering . Springer-Verlag Berlin, Heidelberg, New York, 1978.
- ^ Andre Vander Vorst, Arye Rosen, Youji Kotsuka: RF / Microwave Interaction with Biological Tissues . John Wiley and Sons, Inc., 2006, ISBN 978-0-471-73277-8 , pp. 41 .
- ^ Edward Jordan: Electromagnetic Waves and Radiating Systems . 2nd Edition. Prentice Hall, 1968, ISBN 978-0-13-249995-8 , pp. 130 .
- ↑ Since there is no field in the ladder at the beginning of the process, it cannot be displaced.
- ↑ The opposite arrows suggest an extinction. If one follows the naive explanatory pattern, according to which the eddy currents are caused by the "actual" current, a phase difference of 90 ° should result due to the time derivative in the law of induction. However, this does not allow an erasure.