Ampère's law
The Ampère law ( flux rate , Ampere's law ) is a law of electrodynamics and one of Maxwell's equations . It was discovered by André-Marie Ampère and forms the analogy to the law of induction for magnetism .
Mathematical formulation
Integral form
The law relates the curve integral of the magnetic field along a closed curve to the current that flows through the area enclosed by this curve.
The integral form of the law is (assumption of constant current density is not required):
or.
in which
- the magnetic field, more precisely the magnetic flux density ,
- the magnetic field strength ,
- an infinitesimal , oriented section of the closed curve ,
- the current flowing within
- the permeability of the vacuum ( magnetic field constant ) and
- is the closed curve integral along the curve .
Differential form
The differential form is equivalent to this
or.
is the magnetic field strength , which is the magnetic flux density without taking into account paramagnetic and diamagnetic contributions by the medium (applies in a vacuum ). The current density (current per area) is analogous and the same quantity without taking into account the current induced by para- and diamagnetic effects. is the rotation operator .
The equivalence of integral and differential form is proven by Stokes' theorem.
Maxwell's extension
James Clerk Maxwell noted that Ampère's law so formulated did not initially apply when charging a capacitor , and concluded that the law was incomplete. To solve the problem, he developed the concept of the displacement current and established a general form that is one of Maxwell's four equations. It is given in integral form by
and in differential form
- .
All sizes are as above. is the electric flux density , namely the electric field strength plus the fields generated by polarization.
application
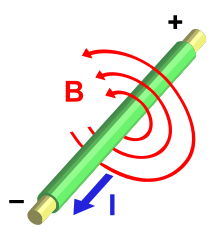
Put simply, Ampère's law says the following: An electric current produces a magnetic field proportional to it , the direction of which forms a clockwise screw with that of the current . See also: right-hand rule .
Interpretation of the integral
The integral formulation
can be interpreted as follows:
A (measuring) frame is placed around a conductor of any shape - be it a wire, a metal plate, a coil, or even just a very small piece of a larger conductor. This frame can be of any shape, e.g. B. a rectangle or a circle of any size. When a current flows through the conductor it creates a magnetic field. If you walk along the frame and add the component of the magnetic field in the direction of the small frame piece for each small piece of the frame, then you get, when the frame is circled, a sum that is proportional to the current through the conductor.
Magnetic field of the coil
With the direct application of Ampère's law to determine a magnetic field, one usually only gets solutions for simplified cases, for example if one assumes that the magnetic field of a coil is homogeneous everywhere along or against the axis of the coil and inside, but this is only for the infinitely long Coil applies.
You have such a coil with turns per section . A rectangular frame is placed through the coil, the upper side of which lies with the length in the coil, and the right and left sides of which are infinitely long. According to the assumption, the magnetic field is perpendicular to these sides, so the component in the direction of the frame is zero. The lower side is infinitely far away, where the magnetic field must be zero. So only the upper side of the integral remains, where the component of the magnetic field is exactly parallel. So:
with which one has determined the amount of the magnetic field in the coil.
Biot-Savart
Simple cases like the one above are not always sufficient to describe magnetic fields induced by currents. In order to be able to deal with any power distribution, the Biot-Savart law provides further information. It can be derived from Maxwell's equations, i.e. H. also that Maxwell's extension of Ampère's law to include the displacement current is necessary for the non-obvious proof.
literature
- Richard P. Feynman, Robert B. Leighton, Matthew Sands: Lectures on Physics. 3. Edition. Oldenbourg Verlag, Munich / Vienna 2001, ISBN 3-486-25589-4 .
- Horst Stöcker: Pocket book of physics. 4th edition. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4 .