Pythagorean addition
A calculation operation similar to the usual addition is called Pythagorean addition , in which the sum of the squares of several sizes is calculated and the square root is formed from this.
Expressed as a formula, the Pythagorean or geometric sum results from the quantities :
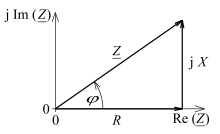
The name of the operation is based on the Pythagorean theorem : if and represent the length of the cathetus and the length of the hypotenuse of a right triangle.
use
Pythagorean addition is used in many areas of science and technology, such as the calculation of the rms value of a current, an alternating current resistance or a measurement uncertainty according to Gaussian error propagation law . Two special features of the calculation can be used here. On the one hand, the terms added to one another are always positive due to the squaring, which means that the result is independent of the sign of the contributing values. On the other hand, the result is always smaller than the usual sum of the amounts (or the result is identical if there is only one value). In the case of the error calculation, the possible mutual compensation of individual random deviations is taken into account. The Pythagorean addition is therefore suitable for estimating the uncertainty of a result in the case of individual values that vary independently of one another.
Furthermore, it is often used as an arithmetic aid, for example to simplify sine and cosine dependent terms with the “ trigonometric Pythagoras ”.