Euclidean norm
The Euclidean norm , standard norm or 2 standard is in the mathematics commonly used vector norm . In two- and three-dimensional Euclidean space , the Euclidean norm corresponds to the descriptive length or amount of a vector and can be calculated using the Pythagorean theorem . More generally, the Euclidean norm is also defined for real and complex vector spaces of any finite dimension and is then the norm derived from the standard scalar product .
As a norm induced by a scalar product , it has a number of other properties in addition to the three norm axioms , such as the validity of the Cauchy-Schwarz inequality and the parallelogram equation , as well as an invariance under unitary transformations . For orthogonal vectors, the Euclidean norm itself satisfies a more general form of the Pythagorean theorem.
Terms such as the Euclidean distance and the Euclidean topology are derived from the Euclidean norm . It can be generalized to infinite-dimensional vector spaces, for example to sequence spaces through the ℓ 2 norm and to function spaces through the L 2 norm .
Definitions
Real vectors in two and three spatial dimensions
A vector in the Euclidean plane can be about its components and in the Cartesian coordinate system by representing. The length or the magnitude of the vector is carried amount strokes characterized by the vector and can with the aid of the Pythagoras' theorem by
be calculated. In three-dimensional Euclidean space, the length of a vector becomes analogous to the two-dimensional case about
determined. In the physics of the amount of a vector sometimes characterized in that omitting the amount of strokes and the vector arrow: . Vectors are in bold in the text, sometimes just the bold is omitted: . The natural length of a vector is also called the Euclidean norm or 2-norm of the vector and, to distinguish it from other vector norms , is denoted by or .
Real vectors of finite dimension
If the vector space is the real -dimensional vectors , then the Euclidean norm of a vector is defined as the root of the sum of the squares of the vector components:
- .
For a one-dimensional vector, the absolute value of a real number results as a special case, and for a two- or three-dimensional vector, its length in the plane or in space is obtained as in the previous section. The Euclidean norm is the standard scalar product of two real vectors
derived because it applies
- .
Complex vectors of finite dimension
If the vector space of the complex -dimensional vectors is now , then the Euclidean norm of a vector is defined as the root of the sum of the squares of the absolute values of the vector components:
- .
The amount bars in the definition must not be left out. A special case for a one-dimensional vector is the absolute value of a complex number corresponding to the length of its vector in the Gaussian plane . The Euclidean norm is the standard scalar product of two complex vectors
induced, where is the conjugate of the complex number . It applies again
- .
Examples
The Euclidean norm of the real vector is
- .
The Euclidean norm of the complex vector is
- .
properties
In the following, the general case of real or complex vectors of finite dimension with or is assumed. The following properties are only special cases of the corresponding properties of general norms induced by a scalar product .
Norm axioms

The Euclidean norm satisfies the three norm axioms . The definiteness
means that if the length of a vector is zero , it must be the zero vector . The absolute homogeneity
states that when the components of a vector are multiplied by a number , the length of the vector changes with the magnitude of that number. The triangle inequality ( subadditivity )
finally states that the length of the sum of two vectors is at most as large as the sum of the two lengths. Equality applies precisely when the two vectors point in the same direction. The proof of the triangle inequality is based on the Cauchy-Schwarz inequality
- .
Unity sphere and unity sphere
The Euclidean norm is a special p -norm for the choice of and is therefore also called the 2-norm. The unit sphere of the Euclidean norm, i.e. the set
the vectors with standard fuel has two real dimensions in the shape of a circle , in three real dimensions the shape of a spherical surface and in general dimensions the shape of a sphere . The amount is called analogously
- or.
the closed or the open unit sphere of the Euclidean norm. It has the shape of a circular disc in two real dimensions and the shape of a sphere in three and higher dimensions . The Euclidean norm can also be defined as a Minkowski functional using its unit sphere .
Parallelogram equation
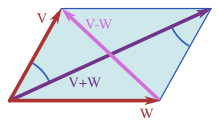
The Euclidean norm is sufficient for all vectors of the parallelogram equation
and is the only p -norm with this property, see also Jordan-von Neumann's theorem .
Unitary invariance
The Euclidean norm is - also as the only p -norm - invariant under unitary transformations . If, therefore, a unitary matrix (in the complex case) or an orthogonal matrix (in the real case) then applies
- ,
what about the displacement property of the standard scalar product
follows. The Euclidean norm does not change under unitary transformations. For real vectors, such transformations are, for example, rotations of the vector around the zero point . This property is for example in the numerical solution of linear least squares problems on the method of least squares means of QR decompositions used.
Derived terms
angle
Using the standard scalar product and the Euclidean norm, the angle between two real vectors can be given by
To be defined. With this angle definition one obtains the following generalization of the cosine law :
- .
There are a number of different definitions for angles between complex vectors. In general, two vectors are said to be orthogonal if their is a scalar product . A more general form of the Pythagorean theorem then applies to orthogonal vectors
- .
Euclidean distance
Furthermore, by means of the Euclidean norm, a metric can be obtained by calculating the difference between two vectors
- ,
the Euclidean metric . A metric allows the distance between two vectors to be measured. Since the Euclidean metric comes from a norm, it is translation-invariant .
Euclidean topology
In addition, a topology , the Euclidean topology, can be defined via the Euclidean norm or metric on the vector space . It is the standard topology that is generated by the system of sets of open spheres
- ,
which contain all vectors with a distance smaller than from a given vector . About this ε-balls can then be as terms of continuity and limit define: for example, aims to sequence of vectors if and only to a limit , if for valid. In fact, all norms on vector space are equivalent to the Euclidean norm and therefore generate the same topology.
Generalizations
If one regards a matrix with real or complex entries as a correspondingly long vector, the Euclidean norm can also be defined for matrices and is then called Frobenius norm . The Euclidean norm can also be generalized to infinitely dimensional vector spaces over the real or complex numbers and then has its own names in part. The most important generalizations are as follows.
ℓ 2 standard
The ℓ 2 -norm is the generalization of the Euclidean norm to the sequence space of quadratically summable sequences . Here only the finite sum is replaced by an infinite one and the ℓ 2 norm is then given as
- .
The space is a Hilbert space with the scalar product of two sequences
- .
L 2 standard
Next the Euclidean norm can be applied to the functional space of on a lot of square-integrable functions generalize what happens in two steps. First, the -norm is a quadratic Lebesgue integrable function as
- ,
defined, whereby in comparison to the ℓ 2 norm only the sum was replaced by an integral. This is initially only a semi-norm , since not only the null function but also all functions that differ from the null function only in terms of a set with Lebesgue measure zero are integrated to zero. Therefore, considering the amount of equivalence classes of functions that are almost the same everywhere, and gets on that L 2 -space the L 2 norm by
- .
The space is a Hilbert space with the scalar product of two functions
- .
It can also be generalized from the Lebesgue measure to general measures .
General vector spaces
The Euclidean norm can be defined even more generally in arbitrary infinite-dimensional vector spaces via an associated Hamel basis . If such a Hamel basis is of , where is an index set , then every vector can be represented as a linear combination with coefficients (here only finitely many of the coefficients are different from 0). The Euclidean norm of a vector is then defined as
and thereby from the scalar product
induced for vectors .
Occasionally, a norm induced by an arbitrary scalar product on a real scalar product space is also called a Euclidean norm.
literature
- Herbert Amann, Joachim Escher : Analysis I . Birkhäuser, Basel 2006, ISBN 3-7643-7755-0 .
- Albrecht Beutelspacher : Linear Algebra . 6th edition. Vieweg, 2003, ISBN 3-528-56508-X .
- Bronstein et al .: Paperback of Mathematics . 7th edition. Harri Deutsch, 2008, ISBN 978-3-8171-2007-9 .
- Gerd Fischer: Linear Algebra . 9th edition. vieweg, ISBN 3-528-57217-5 .
Web links
- Eric W. Weisstein : L ^ 2 norm . In: MathWorld (English).
Individual evidence
- ↑ a b Amann, Escher: Analysis I . 2006, p. 169 .
- ^ Klaus Scharnhorst: Angles in complex vector spaces . In: Acta Applicandae Math. Volume 69 , 2001, p. 95-103 .
- ↑ Scheja, Storch: Textbook of Algebra: Including linear algebra . 2nd volume. Vieweg, 1988, p. 465 .
- ^ Bronstein et al .: Taschenbuch der Mathematik . 2008, p. 368 .
- ↑ Beutelspacher: Linear Algebra . 2003, p. 259 .











































































![[f] \ in L ^ {2} (\ Omega)](https://wikimedia.org/api/rest_v1/media/math/render/svg/a90011eada9282d431f24c351554aac562f9dc41)
![\ | \, [f] \, \ | _ {L ^ {2} (\ Omega)} = \ | f \ | _ {{\ mathcal {L}} ^ {2} (\ Omega)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3acd4af1682b70d5d9cf00c1f4b66e1464a413d)










