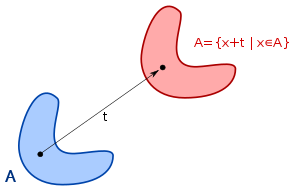
Translational invariance

For translationally invariant functions is . This applies, for example, to the Lebesgue measure.

{\ displaystyle f \ colon \ mathbb {R} ^ {2} \ rightarrow \ mathbb {R}}

{\ displaystyle f (A) = f (A + t)}

The smaller relation on the real numbers is translation invariant.

As translationally invariant in are mathematics figures referred whose value is derived from a translation does not change. More specifically, means a functional translation-invariant, when the value of the functional does not change when the function of a translation with displacement vector is subjected: . ${\ displaystyle F (f) \ to \ mathbb {R}}$ ${\ displaystyle f \ colon \ mathbb {R} ^ {n} \ to \ mathbb {R}}$ ${\ displaystyle a \ in \ mathbb {R} ^ {n}}$ ${\ displaystyle Tf (x) = f (xa)}$

For example, every constant function is translation invariant. A more interesting example is the Lebesgue integral . Its translation invariance clearly means that the value of an integral does not change when the domain of definition is shifted, just as the volume of a body does not change through pure displacement in space.

General definition: translational invariance in groups

More generally, it is possible to define translation invariance in group operations. Let X a set with a transitive operation of a group G . Then induced

{\ displaystyle x \ to gx}

for each element g of G an automorphism of X and thus an automorphism on each functorial structure F (X) on X . The G invariants in F (X) are called translation invariant.

For a group G and X = G one can through

{\ displaystyle h \ to gh}

and

{\ displaystyle h \ to hg ^ {- 1}}

Define two G-spaces, the associated translation invariance is called left or right invariance.

For example, the Lie algebra of a Lie group is the space of the left invariant vector fields . A Haar measure on a topological group is also translation-invariant. The Petersson scalar product on the upper half-plane is defined with the help of an SL (2, R) -invariant measure.

Others

Translation invariant is also a stochastic function that is only changed by additive (or subtractive) components. The laws that are described with the function are not affected. Only the mean or scale values change.

literature

Otto Forster : Analysis. Volume 3: Measure and integration theory, integral theorems in R ⁿ and applications , 8th improved edition. Springer Spectrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5 .
Konrad Königsberger : Analysis 2 , Springer, Berlin 2004.