Network analysis (electrical engineering)

In electrical engineering, network analysis is the procedure for calculating all currents and voltages in a network (see picture) from the known values ​​of the switching elements and the specified source variables. By hand and with analytical methods, only linear systems can be examined with realistic effort. Computer-aided circuit simulation, on the other hand, is mainly based on iterative approximation methods , requires a large number of calculation steps, but can also deal with non-linear components.

Simple electrical network consisting of two meshes and the following components: 2 voltage sources and 4 resistors.

General

In a network, the relationships between all currents and all voltages that occur are described by the kirchhoff rules named after the German physicist Gustav Robert Kirchhoff . The relationship between current and voltage is described by Ohm's law , which describes the component equation of resistors . Real linear switching elements are required, i.e. H. no capacitive or inductive component and a linear characteristic in contrast to z. B. to the diode .

In the case of non-real resistances , the so-called complex calculation is necessary. In this way, an analysis for alternating voltage can also be carried out, with each observed frequency having to be calculated individually.

So that a network analysis is possible, nodes, branches and meshes are defined in the network. With the help of the Kirchhoff rules and the current-voltage relationships of the two-pole equations can then be assigned to them. In order for the mathematical systems of equations to lead to a unique solution, the respective equations must be independent of one another.

Node 1 of the network

A junction is a point in the network at which a flow branch occurs. If a network has nodes, then there are all in all independent node equations. One of these is in the example shown ${\displaystyle k}$ ${\displaystyle (k-1)}$

${\displaystyle I_{1}-I_{2}+I_{3}=0}$.

Branch 1 of the network

A branch is the connection of two nodes by two-pole elements . If the network has branches, then there are also independent branch equations as a whole . ${\displaystyle z}$ ${\displaystyle z}$

In the example shown, the branch equations after utilizing the component equations are:

${\displaystyle U_{z1}=R_{1}\cdot I_{1}-U_{q1}}$

${\displaystyle U_{z2}=R_{2}\cdot I_{2}}$

${\displaystyle U_{z3}=R_{3}\cdot I_{3}+R_{4}\cdot I_{3}-U_{q2}}$

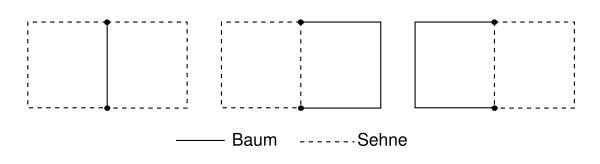
A (complete) tree is a framework of branches that connects all nodes, whereby no node may be touched twice. In clear terms, the structure formed must not offer any opportunities to go in circles. Different variants are possible for the tree. Overall, in a completely meshed network (every node has a branch to every other node), variants are conceivable. In the present example there are three different trees, since more than one branch connects two nodes with one another. ${\displaystyle k^{k-2}}$

The individual branches in the tree are called tree branches or branches . Because of the structure of the tree there are branches. ${\displaystyle a=k-1}$

All branches that do not belong to the tree are called tendons or connecting branches . Their number corresponds to the number of independent mesh equations that can be set up with the help of the mesh set. ${\displaystyle (z-(k-1))}$

Mesh 2 of the network

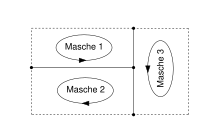
A mesh is a circle closed by branches. For a simple analysis, a circuit should always be chosen over only one tendon or one connecting branch. This path is used for the continuation.

The direction of rotation of the independent meshes can be determined arbitrarily, but is relevant for later calculations. ${\displaystyle m}$

In the example, the following two loops are selected.

${\displaystyle M1\colon \ -U_{q1}+U_{1}+U_{2}=0}$

${\displaystyle M2\colon \ U_{q2}-U_{3}-U_{4}-U_{2}=0}$

Thus there are independent nodal equations, independent mesh equations and a two-pole equation, i.e. two-pole equations, for each branch . With this equation system of equations, all “wanted quantities”, i. H. determine all branch currents and all branch voltages clearly. ${\displaystyle k-1}$ ${\displaystyle m=z-(k-1)}$ ${\displaystyle z}$ ${\displaystyle 2z}$ ${\displaystyle 2z}$ ${\displaystyle z}$ ${\displaystyle z}$

Branch flow analysis

Linear electrical networks
Ideal element
Electrical component
Series and parallel connection
Network transformations
Generator sets	Network sentences
Network analysis methods
Two-port parameters

For the solution by means of branch flow analysis, all independent nodal equations and the independent mesh equations are set up. Then these are sorted by lining them up by current / resistance on one side of the equation and voltages on the other. The result is a linear system of equations.

In the example shown above, this then follows in an orderly order (knot equation 1, mesh equation 1 and mesh equation 2):

${\displaystyle K1\colon \ I_{1}-I_{2}+I_{3}=0}$

${\displaystyle M1\colon \ I_{1}R_{1}+I_{2}R_{2}=U_{q1}}$

${\displaystyle M2\colon \ -I_{2}R_{2}-I_{3}R_{3}-I_{3}R_{4}=-U_{q2}}$

In matrix notation the system of equations is now:

${\displaystyle {\begin{pmatrix}1&-1&1\\R_{1}&R_{2}&0\\0&-R_{2}&-R_{3}-R_{4}\end{pmatrix}}\cdot {\begin{pmatrix}I_{1}\\I_{2}\\I_{3}\end{pmatrix}}={\begin{pmatrix}0\\U_{q1}\\-U_{q2}\end{pmatrix}}}$

There are standard methods that can be used for solving the linear system of equations . Smaller systems of equations can be solved analytically "by hand", for larger circuits numerical methods (computer programs) are used.

Overlay method according to Helmholtz

The superposition method is based on the superposition principle in linear systems.

Action:

• All but one source are removed. Voltage sources are replaced by short circuits or current sources are seen as interruptions. The internal resistances of the sources remain in the circuit.
• The partial flows sought with the remaining source are calculated.
• The process is repeated for each other source.
• Finally, the addition of the calculated partial flows with the correct sign is carried out for the branches under consideration.

Result: The partial flow sought has been determined.

Mesh flow method

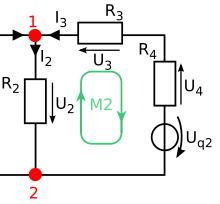
→ Main article : Mesh flow method

With increasing complexity, the effort for calculating the network with branch flow analysis increases. The computational effort is reduced by the mesh flow method (also known as loop analysis).

Vienna bridge

Meshes drawn in the tree diagram

Procedure (short form):

1. Simplify the network
2. Choose a tree, ideal power sources as a tendon
3. Convert non-ideal current sources into an equivalent voltage source
4. Set stitches
5. Setting up the matrix:

   ${\displaystyle {\begin{pmatrix}r_{11}&\dots &r_{1n}\\\vdots &\ddots &\vdots \\r_{n1}&\dots &r_{nn}\end{pmatrix}}\cdot {\begin{pmatrix}i_{M1}\\\vdots \\i_{Mn}\end{pmatrix}}={\begin{pmatrix}u_{qM1}\\\vdots \\u_{qMn}\end{pmatrix}}}$

   ${\displaystyle r_{ii}=\sum R\ in\ M_{i}}$

   ${\displaystyle r_{ij}=r_{ji}=\sum [R\ {\text{in}}\ M_{i}\ {\text{und}}\ M_{j}\cdot {\text{Umlaufsinn}}(M_{i},M_{j})]}$

   ${\displaystyle u_{qMi}=\sum [U_{q}\ {\text{in}}\ M_{i}\cdot (-1)\cdot {\text{Pfeil}}(U_{q},M_{i})]}$

   Special case of ideal current sources (I _q )

   ${\displaystyle {u_{qMi}=\sum [U_{q}\ {\text{in}}\ M_{i}\cdot (-1)\cdot {\text{Pfeil}}(U_{q},M_{i})]-I_{q}\cdot \sum [R\ {\text{in}}\ M_{i}\ {\text{und}}\ M_{Iq}\cdot {\text{Umlaufsinn}}(M_{i},M_{Iq})]}}$

6. Solve system of equations
7. Calculate branch currents based on the sum of the mesh currents

   ${\displaystyle I_{1}=-I_{M2}}$

   ${\displaystyle I_{5}=I_{M1}+I_{M2}}$

Node potential method

→ Main article : Knot potential method

As with the mesh flow method, the node potential method results in a reduced system of linear equations.

Procedure (short form):

1. Convert voltage sources into equivalent current sources
2. Select reference node potential ("ground"), ideal voltage sources connected to reference potential (otherwise this cannot be solved with these instructions)
3. Number the remaining nodes
4. Set up matrix, omit nodes with ideal voltage source

   ${\displaystyle {\begin{pmatrix}g_{11}&\dots &g_{1n}\\\vdots &\ddots &\vdots \\g_{n1}&\dots &g_{nn}\end{pmatrix}}\cdot {\begin{pmatrix}u_{10}\\\vdots \\u_{n0}\end{pmatrix}}={\begin{pmatrix}i_{q1}\\\vdots \\i_{qn}\end{pmatrix}}}$

   ${\displaystyle g_{ii}=\sum G{\text{ mit Knoten }}i{\text{ verbunden}}}$

   ${\displaystyle g_{ij}=g_{ji}=-1\cdot \sum G{\text{ zwischen den Knoten }}i{\text{ und }}j{\text{ (Koppelleitwerte)}}}$

   ${\displaystyle i_{qi}=\sum I_{q}{\text{ an Knoten}}{,}\ I_{q}{\text{vom Knoten weg fließend sind negativ}}}$

5. If the node is coupled to the ideal voltage source, multiply the voltage source by the coupling conductor value and add to the current vector if the voltage arrow points to the reference node potential, otherwise subtract.
6. Solve system of equations.
7. _Determine branch voltage U _ij = u _i0 - u _j0 from the node potentials and use this to obtain the branch _current .

Resistance Cube

Resistance cube made up of twelve equal resistances

One problem in network analysis is the so-called resistance cube , which is formed by twelve equal ohmic resistors soldered together in the shape of a cube . For this construction, the total resistance is to be determined over the room diagonal A'C.

Cube with marked corners and drawn diagonals

The problem can be simplified by considerations of symmetry. The resistor cube is built with twelve equal resistors and is therefore also electrically symmetrical (3-fold rotational symmetry around the spatial diagonal as the axis). Due to the symmetry when a voltage is applied, currents of the same size also flow through the three resistors connected to one another at one corner (only at the corners on the room diagonal). The ends of these three resistors facing away from the corner under consideration are therefore also at the same potential as one another. If points of the same potential, equipotential points, are connected to one another in a conductive manner, no current flows through these connections in the absence of a voltage between them. It follows that these additional connections do not change the circuit. It can also be seen that the same current must flow through the resistors because the same voltage is dropped across them. For example, when determining the total resistance over the corners of the room diagonals (in the graphic, the corners A 'and C), two times three points of equal potential (in the graphic, the points A, B', D 'and B, C', D) that can be connected to each other without causing an electrical change. After making these connections, the clear series connection of a parallel connection of three resistors with a parallel connection of six resistors and a parallel connection of three resistors results .

${\displaystyle R_{\mathrm {ges} }={\frac {1}{3}}\cdot R+{\frac {1}{6}}\cdot R+{\frac {1}{3}}\cdot R={\frac {5}{6}}\cdot R}$

See also

• Network (electrical engineering)
• Norton theorem , substitute power source
• Thévenin's theorem , equivalent voltage source

literature

• Horst Elschner, Albrecht Möschwitzer, Albrecht Reibiger: Computer-aided analysis in electronics ( information electronics series ). Verlag Technik, Berlin 1977.
• Arnold Führer, Klaus Heidemann, Wolfgang Nerreter: Basic areas of electrical engineering. Volume 1: Stationary Processes. Carl Hanser Verlag, Munich a. a. 1983, ISBN 3-446-13677-0 .
• LW Nagel, RA Rohrer: Computer Analysis of Nonlinear Circuits, Excluding Radiation. In: IEEE Journal of Solid State Circuits. Vol. 6, No. 4, 1971, ISSN  0018-9200 , pp. 166-182.
• LW Nagel: Spice 2 - A Computer Program to Simulate Semiconductor Circuits. University of California, Berkeley CA, Erl Memorandum, No. Erl-M520, 1975.
• Jiří Vlach, Kishore Singhal: Computer Methods for Circuit Analysis and Design. 2nd Edition. Van Nostrand Reinhold, New York NY 1993, ISBN 0-442-01194-6 .
• Gert Hagmann: Fundamentals of electrical engineering. 15th edition. AULA publishing house. Wiebelsheim, ISBN 978-3-89104-747-7

Individual evidence

1. ^ Heinrich Hemme : Mathematics for breakfast. 89 math puzzles with detailed solutions. 2nd, revised edition. Vandenhoeck & Ruprecht, Göttingen 2003, ISBN 3-525-40734-3 .