Kirchhoff's rules
| Linear electrical networks | |
|---|---|
| Ideal element | |
| Electrical component | |
| Series and parallel connection | |
| Network transformations | |
| Generator sets | Network sentences |
| Network analysis methods | |
| Two-port parameters | |
The Kirchhoff's laws are within the electrical circuitry in the network analysis used. They are divided into two basic and related sentences, the node sentence and the mesh sentence, and each describe the relationship between several electrical currents and between several electrical voltages in electrical networks. They were formulated in 1845 by Gustav Robert Kirchhoff after they had been discovered by Carl Friedrich Gauß in 1833 .
The node theorem (node rule) - 1. Kirchhoff's law
At a node in an electrical network, the sum of the incoming currents is equal to the sum of the outgoing currents.
If you arrows on all adjacent branch streams in such a way that all associated counting arrows point towards the node or all associated arrows point away from the node, you can write down the node set for a node with branch streams as follows:
This rule initially applies to DC networks.
For alternating current networks it applies on condition that only concentrated components are used and thus, for example, there are no charge storage effects in the nodes and lines due to the capacities available there.
Instead of the time values, one can also look at the vector representations of the currents:
For a network with nodes, linearly independent node equations can be set up.
extension
If one assumes concentrated components, the node rule applies not only to individual nodes, but also to entire circuits. However, it is assumed that the node remains electrically neutral. Would you like B. consider only one capacitor plate (and not the entire capacitor), this requirement is no longer met. In this case one would have to add the so-called displacement current that flows between the capacitor plates. Ampère's law must be used to describe these no longer source-free fields .
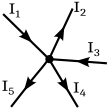
Example of a node
As can be seen in the picture, the currents and flow into the node and the currents , and flow out of the node. The following formula results from the knot rule:
or transformed:
Example of a network node
Entire networks can also be viewed as nodes. In the example, the alternating currents flow into and into the node and the current out of the node.
The following applies:
Are the following complex rms values given for the incoming currents (with the imaginary unit customary in electrical engineering ):
For the outflowing current, the node rule results in:
The set of stitches (rule of stitches) - 2. Kirchhoff's law
All partial voltages of a circuit or a mesh in an electrical network add up to zero. The direction of the rotation can be chosen arbitrarily; but it then defines the signs of the partial voltages. As far as counting arrows point against the direction of rotation, the voltages must be used with the opposite sign.
In a cycle with partial voltages of an electrical network, the following formula applies:
This rule also applies to any time-dependent currents and to networks with non-linear components.
In AC networks, the sum of the complex rms values or complex amplitudes of the voltage can be considered:
In this case, however, the mesh equation only applies to the terminal voltages. This does not correspond to the electric field strength in the components themselves (for example within the coil wire).
A network with branches and independent nodal equations has independent mesh equations.
background
Both Kirchhoff's rules are conclusions from physical conservation laws , the 1st and 3rd Maxwell's equation :
- The node rule describes the conservation of electrical charge and states that charges are neither destroyed nor temporarily stored in the nodes.
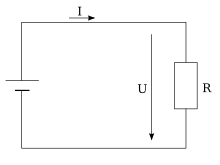
- The mesh rule describes the conservation of electrical energy in electrostatics . This means that a charge does no work on the electric field in a single cycle of the circuit. In the simple circuit opposite, the charges move within the resistance with the electric field, and within the voltage source they move towards the field.
The mesh rule is formally a conclusion from the law of induction . It only applies in the event that there is no change in the magnetic flux within the mesh ( ) and thus no energy is fed into or removed from the network by magnetic means. In the absence of alternating magnetic fields, the law of induction delivers
- ,
which corresponds exactly to the statement of the mesh rule. The term denotes the circulating voltage for a path that bypasses the components but contains their poles .
When using the kirchhoff equations, it should generally be noted that all connections between the individual circuit elements are assumed to be ideally conductive. In addition, the components are considered to be concentrated components. Concentrated components can be fully described in their electrical behavior by the currents flowing at the connections and external voltages. If there are non-concentrated components in the circuit to be examined, these must be replaced by equivalent circuits of concentrated circuit elements.
The presentation of the general Kirchhoff rules has been modified in various ways for practical applications. Among other things, Millman's sentence, which is common in English-speaking countries, describes a method based on Kirchhoff's rules to determine the total voltage of several voltage and current sources connected in parallel .
Detection of time-varying external magnetic fields
If through the mesh of a network with field-encapsulating passive or active elements (e.g. resistors, capacitors, coils, diodes, electric motors, power plant generators, electrochemical cells, thermocouples, photocells, etc.) external (not excited by the currents of the network) time-varying flows step, the main requirement of Kirchhoff's mesh theorem is (namely ) violated. Then the voltage equation that can be derived with the law of induction applies to a mesh
- .
The left side of the equation is exactly as above (i.e. without an external magnetic field) using the terminals to form voltages of the elements. The direction of rotation of the summation can no longer be chosen arbitrarily, but must be oriented clockwise with the reference direction of the magnetic flux.
The case occurs z. B. in geomagnetically induced currents .
literature
- Karl Küpfmüller , Gerhard Kohn: Theoretical electrical engineering and electronics . 14th edition. Springer, 1993, ISBN 3-540-56500-0 .
- Gustav Robert Kirchhoff : About the passage of an electric current through a plane, especially through a circular one . In: Annals of Physics and Chemistry . tape LXIV , 1845, p. 497-514 ( Gallica ).
- Gert Hagmann: Fundamentals of electrical engineering. 15th edition. AULA publishing house. Wiebelsheim, ISBN 978-3-89104-747-7
Web links
- Kirchhoff - Laws at Student Level ( LEIFI )
- electronics compendium
- wisc-online (english)
- facstaff.bucknell (English)
Individual evidence
- ↑ Gustav Robert Kirchhoff: About the passage of an electric current through a plane, especially through a circular one. In: Annals of Physics and Chemistry . Volume LXIV, 1845, p. 513 ( Gallica ).
- ^ Dunnington: Gauss - Titan of Science. American Mathematical Society, p. 161.
- ↑ Richard P. Feynman, Robert B. Leighton, Matthew Sands: Electromagnetism and the structure of matter . Definitive Edition (= Feynman lectures on physics . Volume II ). 5th, improved edition. Oldenbourg Verlag, Munich; Vienna 2007, ISBN 978-3-486-58107-2 , section 22.3, p. 419 f . ( The Feynman Lectures on Physics Website - English: The Feynman Lectures on Physics . 2006. Translated by Marlis Mitter).
- ↑ This refers to elements whose electromagnetic fields are only noticeable to the outside through negligible scattering effects.