Oriented surface

Two normal unit vectors of a flat surface.

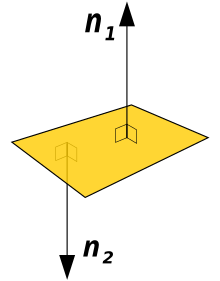
A oriented surface is in the mathematical sub-area of the elementary differential geometry an orientable surface for which it was determined which of its two sides, the outer or inner side. The orientation of a surface is determined by choosing one of the two possible surface normal vectors. The outside of the surface is that from which the chosen normal vector leads away. There are areas that cannot be oriented, such as the Möbius strip .

definition

A regular surface with a continuous unit normal field

A regular surface (or a regular surface with a border) is called orientable if there is a continuous unit normal vector field on . ${\displaystyle S\subset \mathbb {R} ^{3}}$ ${\displaystyle S}$

Such a continuous unit normal vector field on defines an orientation of . An oriented surface is thus an orientable surface on which a continuous unit normal vector field has been selected. Formally an oriented surface is a pair of an orientable surface and a steady unit normal vector field on . ${\displaystyle {\vec {n}}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle (S,{\vec {n}})}$ ${\displaystyle S}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle S}$

If the continuous unit normal vector field gives an orientation on the surface , then there is also a continuous unit normal vector field which defines a further orientation of . If the orientable surface is contiguous , then there are precisely these two orientations. If the surface consists of several related components, an orientation can be selected on each related component independently of the others. ${\displaystyle {\vec {n}}_{1}}$ ${\displaystyle S}$ ${\displaystyle {\vec {n}}_{2}=-{\vec {n}}_{1}}$ ${\displaystyle S}$ ${\displaystyle S}$

If an orientation is selected on a surface, it is designated as positive , the opposite orientation as negative .

Intuition

Closed areas

A coherent closed surface , such as a sphere ( spherical surface ) or a torus , divides the space into two coherent parts, the interior and the exterior. Accordingly, one speaks of the inside and the outside of the surface. A selection of the outside corresponds to an outward-pointing, and a selection of the inside corresponds to an inward-pointing unit normal vector field. Unless otherwise stated, the orientation is chosen by an outward-pointing unit normal vector field. This is a prerequisite for the application of the Gaussian integral theorem .

Areas with a border

An oriented surface with a border and the associated direction of its border curve.

In the case of surfaces with a border, an orientation (direction of passage ) of the boundary curve (s) is determined by an orientation of the surface .

Descriptive: If you consider the selected side of the surface as "above" and imagine an observer walking along the edge on the upper side of the surface so that the surface is to the left of him, the observer traverses the curve in a positive direction . It is said that the direction of rotation of the edge curve with the surface normal forms a right-hand screw or a right-hand screw, since a right-hand screw parallel to the surface normal would advance in the direction of the surface normal when rotating in the direction of the surface. If the area is limited by a single edge curve, conversely a direction of passage of the edge curve determines an orientation of the area.

With the classical integral theorem of Stokes it is assumed that the orientation of the surface and the direction of passage of the boundary curve (s) are related in the mentioned way.

Oriented levels

A plane in three-dimensional space divides this into a positive and negative half-space , whereby the orientation of the plane (with the exception of the undefined special case of the original plane ) is chosen where the coordinate origin lies in the negative half-space, i.e. the normal vector of the plane in the direction of the positive Half space shows. ${\displaystyle \mathbb {R} ^{3}}$

Oriented levels play e.g. B. in distance calculations with the help of the Hessian normal form of the vector plane equation a role.

If one generalizes the idea of ​​the plane in three-dimensional space to that of the hyperplane in n-dimensional space , one can also calculate with oriented hyperplanes of higher or lower dimensions. In two-dimensional space, for example, this is an oriented straight line that divides the space into two half-planes , with the normal vector of the straight line also in this case by definition pointing into the positive half-space (here the positive half- plane ), i.e. ( apart from the undefined special case of the straight line through the origin ) also here away from the origin of coordinates. In contrast, hyperplanes of higher dimensions can be found e.g. B. in solving certain business mathematical questions. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{2}}$

Relevance in physics and mathematics

The agreement of the orientation of a surface is particularly important when calculating vector surface integrals , e.g. B. in electrostatics when using the Gaussian integral theorem . The orientation determines the sign of the result. Would you like If, for example, you calculate the charge Q within a given volume and only the electric field on the surface of the volume is known, you can use this theorem to infer the enclosed charge. ${\displaystyle {\vec {E}}({\vec {x}})}$

${\displaystyle Q=\int _{V}\mathrm {d} V\varrho ({\vec {x}})=\varepsilon _{0}\int _{V}\mathrm {d} V\mathrm {div} {\vec {E}}({\vec {x}})}$.

Here, V is the volume in which the unknown charge is contained and the unknown charge density . With the help of the first Maxwell equation one gets to the expression on the right side, with the dielectric constant and div the divergence . With the help of the Gaussian integral theorem, the volume integral can now be reformulated into a surface integral : ${\displaystyle \varrho }$ ${\displaystyle \varepsilon _{0}}$

${\displaystyle Q=\varepsilon _{0}\int _{\partial V}\mathrm {d} {\vec {A}}\cdot {\vec {E}}({\vec {x}})}$.

${\displaystyle \mathrm {d} {\vec {A}}}$is an infinitesimally oriented area element of the surface of the volume. The sign of the scalar product depends on the direction of . Is parallel to , then is the scalar product , on the other hand, if both vectors are anti-parallel, then is the scalar product . The sign of the surface integral therefore depends on the selected orientation of the surface. The choice of a positive orientation was agreed as a convention , that is, the outward-pointing unit normal vector field (see above) is chosen as the orientation of a surface. ${\displaystyle \partial V}$ ${\displaystyle \mathrm {d} {\vec {A}}\cdot {\vec {E}}}$ ${\displaystyle \mathrm {d} {\vec {A}}}$ ${\displaystyle \mathrm {d} {\vec {A}}}$ ${\displaystyle {\vec {E}}}$ ${\displaystyle \mathrm {d} A\,E}$ ${\displaystyle -\mathrm {d} A\,E}$

Individual evidence

1. ^ Ilja N. Bronstein, KA Semendjajew: Taschenbuch der Mathematik . Harri Deutsch Verlag, 2008, ISBN 978-3-8171-2007-9 , pp. 538 ( online [accessed August 24, 2012]).
2. ↑ Rolf Schloms: Understanding Physics: An Introduction to the Mindset of Physics. Homogeneous Systems . Oldenbourg Verlag, 2008, ISBN 978-3-486-58582-7 , pp. 107 ( online [accessed August 24, 2012]).
3. ↑ Thoralf Räsch: Mathematics of Physics for Dummies . John Wiley & Sons, 2011, ISBN 978-3-527-70576-4 , pp. 398 ( online [accessed August 24, 2012]).
4. ↑ Christian Bär : Elementary differential geometry. de Gruyter, Berlin a. a. 2001, ISBN 3-11-015519-2 , pp. 117-118.
5. ↑ James Stewart: Multivariable Calculus . Cengage Learning, 2011, ISBN 978-0-538-49787-9 , pp. 1140 ( online [accessed August 24, 2012]).
6. ↑ Kurt Meyberg, Peter Vachenauer: Higher mathematics 1: differential and integral calculus. Vector and matrix calculations . Springer, Berlin, Heidelberg 2001, ISBN 978-3-642-56654-7 , pp. 482 ( books.google.de [accessed January 4, 2014]).
7. ↑ Gregor M. Fichtenholz: differential and integral calculus . Harri Deutsch Verlag, 1992, ISBN 978-3-8171-1280-7 , pp. 219 ( online [accessed August 24, 2012]).