Hessian normal form

The HNF , Hesse normal form or hess ash normal form is in mathematics a special form of a linear equation or plane equation . The Hessian normal form is often used to calculate the distance between a point and a straight line (im ) or a plane (im ). It is named after the German mathematician Otto Hesse . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{3}}$

Hessian normal form of a straight line equation

Hessian normal form of the straight line equation ${\displaystyle {\tfrac {1}{\sqrt {5}}}\,x+{\tfrac {2}{\sqrt {5}}}\,y={\tfrac {6}{\sqrt {5}}}}$

presentation

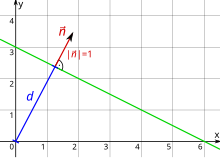
In the Hessian normal form, a straight line in the Euclidean plane is described by a normalized normal vector (normal unit vector) of the straight line and its distance from the origin of coordinates. A straight line then consists of those points in the plane whose position vectors give the equation ${\displaystyle {\vec {n}}_{0}}$ ${\displaystyle d\geq 0}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}=d}$

fulfill. Here is the scalar product . ${\displaystyle \cdot }$

The normal vector is a vector that is orthogonal to a straight line; H. forms a right angle with it.

As a normal unit vector, it must have the length and it must point from the coordinate origin in the direction of the straight line, so it must apply. ${\displaystyle |{\vec {n}}_{0}|=1}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}\geq 0}$

In the Hessian normal form, the points of the straight lines are therefore implicitly defined in that the scalar product of the position vector of a straight line point and the normal vector of the straight line is equal to the distance of the straight line from the origin. A point whose position vector does not satisfy the equation lies on that side of the straight line into which the normal vector points, and otherwise on the other side. The origin of the coordinates is always on the negative side of the straight line, provided it is not a straight line through the origin . ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}>d}$

example

If a normal unit vector of a straight line is the distance between the straight line and the origin, the normal form is obtained ${\displaystyle {\vec {n}}_{0}={\begin{pmatrix}3/5\\4/5\end{pmatrix}}}$ ${\displaystyle d=1{,}2}$

${\displaystyle {\tfrac {3}{5}}\,x+{\tfrac {4}{5}}\,y=1{,}2}$.

Each choice of which satisfies this equation, for example or , then corresponds to a straight line point. ${\displaystyle (x,y)}$ ${\displaystyle (2,0)}$ ${\displaystyle (-2,3)}$

calculation

From the normal form of a straight line equation with support vector and normal vector , a normalized and signed normal vector of the straight line can be passed through ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {n}}_{0}={\begin{cases}{\frac {\vec {n}}{|{\vec {n}}|}}&{\text{falls}}~{\vec {p}}\cdot {\vec {n}}\geq 0\\-{\frac {\vec {n}}{|{\vec {n}}|}}&{\text{falls}}~{\vec {p}}\cdot {\vec {n}}<0\end{cases}}}$

determine. The distance of the straight line from the origin can then be through

${\displaystyle d={\vec {p}}\cdot {\vec {n}}_{0}}$

be determined. This distance corresponds to the length of the orthogonal projection of the vector onto the straight line through the origin with the direction vector . ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}_{0}}$

From the other forms of straight line equations, the coordinate form , the intercept form , the parameter form and the two-point form , the associated normal form of the straight line is first determined (see calculation of the normal form ) and then the Hessian normal form.

Distance calculation

With the help of the Hessian normal form, the distance of any point in the plane from a straight line can be calculated simply by inserting the position vector of the point into the straight line equation: ${\displaystyle Q}$ ${\displaystyle g}$ ${\displaystyle {\vec {q}}}$

${\displaystyle d(Q,g)={\vec {q}}\cdot {\vec {n}}_{0}-d}$.

This distance is signed : for the point lies on the side of the straight line into which the normal vector points, otherwise on the other side. ${\displaystyle d(Q,g)>0}$ ${\displaystyle Q}$

Alternatively, you can use the absolute amount :

${\displaystyle d(Q,g)=|{\vec {q}}\cdot {\vec {n}}_{0}-d|}$

or even use the (non-normalized) normal vector:

${\displaystyle d(Q,g)=\left|{\frac {{\vec {q}}\cdot {\vec {n}}-d}{|{\vec {n}}|}}\right|}$

Hessian normal form of a plane equation

Hessian normal form of a plane equation

presentation

Similarly, a plane in three-dimensional space is described in the Hessian normal form by a normalized and (possibly with a sign) normal vector of the plane and its distance from the coordinate origin. A plane then consists of those points in space whose position vectors give the equation ${\displaystyle {\vec {n}}_{0}}$ ${\displaystyle d\geq 0}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}=d}$

fulfill. The normal vector here is a vector that is perpendicular to the plane. The normal vector must again have the length and point from the origin of coordinates in the direction of the plane, so it must apply. ${\displaystyle |{\vec {n}}_{0}|=1}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}\geq 0}$

In the Hessian normal form, the points of the plane are therefore implicitly defined in that the scalar product of the position vector of a plane point and the normal vector of the plane is equal to the distance of the plane from the origin. Again, a point whose position vector satisfies the equation lies on the plane. If so , then the point lies on that side of the plane into which the normal vector points, otherwise on the other side. The origin of coordinates is always on the negative side of the plane, unless it is an origin plane . ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}>d}$

example

For example, if there is a normalized normal vector of a given plane and the distance between the plane and the origin , then the plane equation is obtained ${\displaystyle {\vec {n}}_{0}={\begin{pmatrix}{\tfrac {2}{3}}\\{\tfrac {1}{3}}\\-{\tfrac {2}{3}}\end{pmatrix}}}$ ${\displaystyle d={\tfrac {4}{3}}}$

${\displaystyle {\tfrac {2}{3}}\,x+{\tfrac {1}{3}}\,y-{\tfrac {2}{3}}\,z={\tfrac {4}{3}}}$.

Any choice of that satisfies this equation, for example or , then corresponds to a plane point. ${\displaystyle (x,y,z)}$ ${\displaystyle (1,2,0)}$ ${\displaystyle (2,-2,-1)}$

calculation

A normalized and signed normal vector of the plane can be derived from the normal form of a plane equation with support vector and normal vector , as in the two-dimensional case ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {n}}_{0}={\begin{cases}{\frac {\vec {n}}{|{\vec {n}}|}}&{\text{falls}}~{\vec {p}}\cdot {\vec {n}}\geq 0\\-{\frac {\vec {n}}{|{\vec {n}}|}}&{\text{falls}}~{\vec {p}}\cdot {\vec {n}}<0\end{cases}}}$

determine. The distance of the plane from the origin can then be through

${\displaystyle d={\vec {p}}\cdot {\vec {n}}_{0}}$

be determined. This distance in turn corresponds to the length of the orthogonal projection of the vector onto the straight line through the origin with the direction vector . ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}_{0}}$

From the other forms of plane equations, the coordinate form , the axis intercept form , the parameter form and the three-point form , the associated normal form of the plane is first determined (see calculation of the normal form ) and then the Hessian normal form.

distance

With the help of the Hessian normal form, the distance of any point in space from a plane can in turn be calculated by inserting the position vector of the point into the plane equation: ${\displaystyle Q}$ ${\displaystyle E}$ ${\displaystyle {\vec {q}}}$

${\displaystyle d(Q,E)={\vec {q}}\cdot {\vec {n}}_{0}-d}$.

This distance is again signed: for the point lies on that side of the plane into which the normal vector points, otherwise on the other side. ${\displaystyle d(Q,E)>0}$ ${\displaystyle Q}$

Alternative formulation with a support vector

Although the distance calculation using the Hessian normal form is often taught using a distance to the coordinate origin, a similar Hessian normal form with a support vector is occasionally used . ${\displaystyle d}$

The Hessian normal form of a plane is then:

${\displaystyle E\colon \,({\vec {x}}-{\vec {a}})\cdot {\vec {n}}_{0}=0}$,

where is a support vector of the plane. ${\displaystyle {\vec {a}}}$

Distance formula

This then results in the distance formula for a point with the position vector from the plane with the support vector and the normal unit vector ${\displaystyle {\vec {p}}}$ ${\displaystyle E}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {n}}_{0}}$

${\displaystyle d=|({\vec {p}}-{\vec {a}})\cdot {\vec {n}}_{0}|}$.

Generalization for hyperplanes

In general, the Hessian normal form describes a hyperplane in -dimensional Euclidean space. In -dimensional Euclidean space, a hyperplane consists of those points whose position vectors correspond to the equation ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}=d}$

fulfill. It is only calculated with -component instead of two- or three-component vectors. A hyperplane divides the -dimensional space into two parts called half-spaces . A point whose position vector satisfies the equation lies exactly on the hyperplane. If so , then the point lies in that half-space into which the normal vector points, otherwise in the other. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}_{0}>d}$

See also

• Ascoli's formula

literature

• Lothar Papula : Mathematical formula collection: For engineers and natural scientists . Springer, 2009, ISBN 978-3-8348-9598-1 .
• Harald Scheid , Wolfgang Schwarz: Elements of linear algebra and analysis . Springer, 2009, ISBN 978-3-8274-2255-2 .

Individual evidence

1. ^ Anton Bigalke, Norbert Köhler (Ed.): Mathematics. Grammar school upper level Berlin basic course ma-3 . Cornelsen Verlag, Berlin 2011, ISBN 978-3-06-040003-4 , pp. 137 .