Mechanical tension
| Physical size | |||||||
|---|---|---|---|---|---|---|---|
| Surname | mechanical tension | ||||||
| Formula symbol |
(Normal stresses), (shear stresses) |
||||||
|
|||||||
| See also: pressure p | |||||||
The mechanical stress (symbols σ (small sigma ) and τ (small tau ), English stress , French contrainte ) is a measure of the internal stress on a body as a result of its external stress . Since there is no risk of confusion with electrical voltage within mechanics , it is briefly referred to as voltage .
The mechanical normal stress σ on an imaginary sectional surface A ( area ) through a body is the related component F n of an external force F ( force ) acting perpendicularly on it :
- .
The mechanical shear or shear stress τ in an imaginary sectional area A through a body is the related component F A (transverse force) of an external force F :
- , (Approximation equation: shear stress is not constant over the surface and is always zero at the surface).
The mechanical tension has the same physical dimension as the pressure , namely force per unit area . In liquids and gases at rest, pressure is a normal stress that acts equally in all spatial directions.
In mechanical engineering and structural engineering , the dimensioning of objects requires knowledge of the mechanical stresses that occur. The mechanical stresses occur as components of the stress tensor in physical laws.
Cutting stresses
By applying the cutting principle , internal stresses in a body can be shown clearly. The cutting forces that result from the forces acting on the body from outside and allow conclusions to be drawn about the internal stresses on the body are applied to an imaginary cut at any point on a body.
Normal, bending, shear, torsional stress and true stress
With a uniform tensile or compressive load on a rod , the stress is evenly distributed over the cross-sectional area. The normal stress, i.e. H. the stress under normal force loading due to tension or compression results from
where the force is in the direction of the surface normal and the area of the rod cross-section. For the true stresses this is the area of the deformed bar and for the nominal or engineering stresses the nominal value of the undeformed initial bar cross-section , see tensile test . The stress tensor always has 3 normal stress components (for all three spatial directions); if this is positive in one spatial direction, there is tension in this spatial direction, and in the case of compressive stresses, the normal stress component in this direction is negative.
When the rod is subjected to bending stress, the result is a bending stress that is highest at the edge of the rod cross-section (in the so-called edge fiber ) and decreases to zero towards the center (in the so-called neutral fiber ). In summary, the bending stress is the compressive and tensile stress caused by the bending in a part of the cross-section:
With constant uniaxial bending in the main axis of inertia , the formula is simplified to:
wherein the bending moment around the y-axis, the area moment of inertia about the y-axis, the distance from the neutral fiber (with σ B = 0), the maximum or minimum occurring distance between the focal axis to extreme fiber and the moment of resistance is, see beam theory . The following sketch illustrates this using a cantilever :
As a vector , the cutting stress vector has three components that depend on the orientation of the cutting surface. The vertical arrows on the cutting edges indicate shear stresses introduced by the transverse force . In the case of a profile loaded with a transverse force, as shown in the picture, a non-constant shear stress curve occurs over the cross-section. If the transverse force acts outside the center of shear , torsion also occurs.
In the case of torsion of bars with a circular (ring) cross-section, the shear stress is:
Therein, M t , the torsional moment , I p , the polar moment of inertia , W t , the torsional moment of resistance , r the radial Zylinderkoordinate and r a is the outer radius of the (hollow) cylinder.
The formulas for bending and torsional stress assume linear elasticity .
The tensor calculation allows the stress state to be described initially independently of a certain coordinate system and only after a derivation of the respective calculation method (such as the formulas above) to adapt the geometric properties of the body, for example in cylinder coordinates as in the case of torsion.
Stress, stress vector and stress tensor
The stresses acting at a certain point are described in their entirety by the stresses in three intersecting surfaces that intersect at the point, i.e. by three stress vectors with three stress-like components each. The three stress vectors taken together form the stress tensor defined by Augustin-Louis Cauchy . The orientation of the cut surfaces is arbitrary as long as their normals are linearly independent , because as a tensor the stress tensor is independent of the selected base system . As an example, the three cut surfaces can each be selected perpendicular to a direction of a Cartesian coordinate system with x, y and z coordinates. The three stress vectors on the three cut surfaces then correspond to the rows of the following matrix with the stresses as their components:
With regard to the standard basis , it corresponds to the stress tensor. The meaning of the indices is shown in the sketch of a volume element that has been cut out. In the double index , the first index indicates the direction in which the normal vector of the cutting surface points, and the second index indicates in which direction the stress acts. The stress tensor, multiplied by the normal unit vector of a section surface, gives the stress vector on this surface (force vector per unit area):
With the “current” or “true” Cauchy stresses, the matrix is symmetrical , so that, for example, τ xy = τ yx and therefore the transposition (·) T can be omitted in the above formula .
If the stress matrix is set up in a different coordinate system, then its components change in a characteristic way, just as the components of a geometric vector change when the base system changes. However, the amount of the vector does not change and the stress tensor also has so-called invariants that do not change when the base is changed. The following invariants are particularly important for the stress tensor:
- the pressure , which is the negative mean of the diagonal elements and which is proportional to the trace of the stress matrix ,
- the von Mises equivalent stress that is an invariant of the stress deviator , is
- the principal stresses and
- the maximum shear stresses, see below .
Shear, compressive and tensile stress
The diagonal elements σ xx , σ yy , σ zz in the stress matrix represent the normal stresses , i.e. the stresses that act perpendicular to the coordinate surface. In other words: the normal and effective directions are the same.
Normal stresses are called tensile stress (positive sign) or compressive stress (negative sign) , depending on the sign . Compressive stress is sometimes also referred to as surface pressure .
In contrast to compressive stress , pressure is exclusively isotropic . This means that pressure is not a vector , but the negative hydrostatic part of the stress tensor . It acts in all directions at the same time and is therefore the negative mean value of the normal stresses in the three spatial directions ( ). It is positive with hydrostatic pressure and negative with hydrostatic pull. (The latter can only occur in solids, since the apparent hydrostatic pull in a vacuumed vessel is actually pressure that acts on the vessel from the outside.)
The off-diagonal elements τ ij are called shear stresses . They act tangentially to the surface, so they represent a shear load .
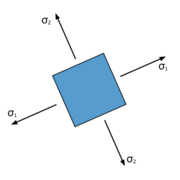
Principal stress and direction of principal stress
For every state of stress in equilibrium, three pairs of perpendicular directions can be found by transformation of the principal axes , in which no shear stresses occur during tension and compression, see pictures. The main stresses σ 1,2,3 act in these main stress directions .
The principal stresses can be calculated by solving the equation , where E is the 3 × 3 identity matrix . Multiplying the determinant det leads to an equation of the third degree in σ, the solutions of which represent the principal stresses sought. They are the eigenvalues of the stress matrix S and are all real because the matrix is symmetrical. A hydrostatic stress state exists when the three principal stresses are equal. (There are no shear stresses here.)
The respective main stress direction results from the equation , whereby the calculated main stress is used. The solutions are eigenvectors of the stress matrix S and indicate the direction of the principal stresses. In normalized form, they form an orthonormal basis of three-dimensional space or can be orthogonalized accordingly. In the main stress directions, the cutting stresses are extremal. The family of curves of the main stress lines are called stress trajectories .
The Mohr stress circle gives a graphic impression of the dependence of the normal and shear stress on the normal direction in the plane spanned by two main stress directions. The main shear stresses
are critical shear stresses and occur in cutting planes that are normal to the bisector between the main stress directions. Let σ 1 be the greatest and σ 3 be the smallest principal stress. Then is the maximum shear stress
The xy-plane will be spanned by the 1 and 2 main stress directions as in the pictures. Then the principal stresses and the principal shear stress for a given stress state are in this plane
The angle to the x-axis at which the principal stresses occur is
Relationships in strength theory
A real body exposed to tension deforms.
Hooke's law establishes the relationship to deformation for elastic deformations . The most important material constants are the modulus of elasticity , shear modulus and Poisson's ratio .
The plastic deformation is described by the flow condition , the flow law and the hardening law. In the main stress space, in which the main stresses are plotted on the coordinate axes, a stress state represents a point or a vector that can be broken down into two components:
- The (deviatoric) component transversely to the diagonal of the space in the main stress area, i.e. transversely to the hydrostatic stress component, is a measure of how large the maximum shear stresses can be depending on the cutting direction. This proportion alone is relevant when calculating steel structures . It corresponds to the von Mises equivalent stress after the change of shape hypothesis and is a function of the amount of the stress deviator . When this comparison voltage, the yield stress exceeds the steel, deforms the steel plastically .
- The component in the direction of the room diagonal describes the pressure; this part is irrelevant when calculating steel structures, since it does not lead to shear stresses in any cutting direction and therefore also to no plastic deformation .
A solid body can also have internal stresses that occur without external forces acting on the body.
In general, the deformation behavior of a body depends on its shape and the properties of the materials from which it is made. The material properties are described mathematically in a material model by a relationship between stress and strain tensor as well as their rates and time courses. With the material models, the stresses in it can be calculated for a given body, its bearings and loads. The rheology , materials science and theory of materials dealing with the flow and deformation behavior of materials and make it possible tensions calculation to determine.
Relationships in fluid mechanics
Newton's viscosity approach establishes the relationship to the rate of deformation in linear-viscous liquids and gases ( fluids ) . The most important material constant is the dynamic viscosity . The cause of the viscosity is the friction and the impulse transport between the fluid elements.
With laminar flow and a sufficiently large Reynolds number , the viscosity of the flowing fluid can be neglected in the majority of a flow field . Here the dominant stress in the fluid is pressure. The total pressure is divided into dynamic and static pressure . The dynamic pressure is fed from the kinetic energy of the fluid elements. The static pressure is the pressure felt by a fluid element moving with the flow. It is described in gases with equations of state and in the case of the ideal gas by gas laws .
The influence of the viscosity in the boundary layer on walls around which the flow is flowing should not be neglected . The thickness of this boundary layer is very small when the flow is present, but the wall shear stress creates the shear stress resistance of the flow around it, which together with the pressure resistance makes up the entire flow resistance of a body.
When the boundary layer separates , the wall shear stress can disappear or even act against the external flow. Such detachments can have dramatic effects when they occur on airfoils or in jet engines .
literature
- H. Balke: Introduction to Technical Mechanics. Strength theory . 3. Edition. Springer-Vieweg, 2014, ISBN 978-3-642-40980-6 .
- Heinz Parkus: Mechanics of Solid Bodies . 2nd edition, 6th reprint. Springer, Vienna / New York 2009, ISBN 978-3-211-80777-4 .
- Christian Spura: Technical Mechanics 2. Elastostatics . 1st edition. Springer, Wiesbaden 2019, ISBN 978-3-658-19979-1 .
Individual evidence
- ↑ H. Balke: Introduction to Technical Mechanics. Strength theory. 2014, p. 32.
- ↑ Herbert Mang , Günter Hofstetter: Strength theory . 3. Edition. Springer Verlag, Vienna / New York 2008, ISBN 978-3-211-72453-8 , 6.4 "Normal stresses", p. 156 ( springer.com ).
- ↑ H. Balke: Introduction to Technical Mechanics. Strength theory. 2014, p. 63ff.