Wall shear stress
The wall shear stress (formula symbol , dimension ML −1 T −2 , English wall shear stress ) is in fluid mechanics the tangentially acting force per surface area exerted by a fluid (liquid or gas) on walls and according to this definition it has a direction. The wall shear stress is the momentum flow through the volume of the fluid adjoining the wall and results from the friction of the fluid elements on the wall and with one another. In fluid mechanics, both the directional, vector shape and its amount are referred to as wall shear stress.
The wall shear stress is a central parameter in boundary layer theory and aerodynamics and is used to determine the shear stress resistance .
definition
The wall shear stress is defined as the quotient of the parallel force that a fluid exerts on a wall and the area of the wall:
With
In contrast to pressure , the wall shear stress is a vectorial (directed) quantity.
If the basis vector points in the direction of the wall shear stress, then the component of the vectorial wall shear stress becomes in the effective direction
also briefly referred to as wall shear stress.
Influence of the fluid properties

When fluid elements brush along a wall, they are carried along by the wall due to friction effects, that is, their speeds tend to equalize one another. The fluid element transmits momentum to the wall, which thereby experiences a force. Conversely, the wall also exerts a force on the fluid, the speed of which changes as a result. If these forces are related to their effective surface, then tensions arise . In a continuum flow, the fluid elements and the wall exchange momentum via the stresses acting between them.
The Newtonian fluids are the fluids mostly considered in fluid mechanics and in them the wall shear stress is proportional to the speed difference perpendicular to the flow direction parallel to the wall:
As in the picture, the fluid flows in the x-direction and the y-direction is perpendicular to the wall and has its origin on the wall. The proportionality constant η is the dynamic viscosity (dimension ML –1 T −1 , unit Pa s ).
In non-Newtonian fluids, the relationship between wall shear stress and flow velocity is not linear.
In ideal liquids and gases , the fluid elements do not rub against each other and their effect on the wall is exclusively perpendicular to the wall. Accordingly, there are no shear stresses in the fluid and the wall shear stress is always zero on all walls.
Continuum mechanical consideration
The cutting stresses in the fluid and at its limits result from the Cauchy stress tensor in continuum mechanics (dimension ML −1 T −2 , unit Pa ). The shear stresses are the secondary diagonal members of the stress tensor. The stress vector on the wall with normal vector is then the product. When the stress vector is freed from its component in the y-direction, the vectorial wall shear stress remains
and the scalar product with the basis vector in the x-direction gives the scalar wall shear stress
The Cauchy's stress tensor fulfills the momentum balance and acts back on the velocity field via the material properties of the fluid.
Quantities derived from the wall shear stress
Wall shear stress velocity
In flows near walls or in pipes, dominated by boundary layer effects, is the wall shear stress velocity
a characteristic speed (dimension LT −1 , unit m / s ). The denominator of the fraction is the density of the fluid near the wall.
Dimensionless coordinate
With the wall shear stress velocity, a dimensionless coordinate
which is important when modeling turbulent boundary layers. The parameter is the kinematic viscosity (dimension L 2 T −1 , unit m² / s ) of the fluid.
Coefficient of friction
Another important figure in boundary layer flows is the dimensionless coefficient of friction c f . It is the ratio of the wall shear stress to the dynamic pressure of the external flow with flow velocity :
Separation points
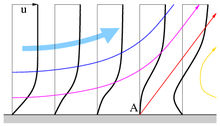
If the pressure near a wall increases in the direction of flow, the external flow is decelerated and slower fluid elements near the wall are slowed down even more by the friction. If the delay is large enough, a backflow area occurs in which eddies form (orange in the picture on the far right) and the flow separates from the wall. At the separation point A, a streamline (red) leaves the wall at a certain angle and forms a separating layer between the laminar and the turbulent flow. When a turbulent boundary layer forms, it is thickened by the eddies (blue line).
The separation point is where the gradient of the velocity parallel to the wall disappears perpendicular to the wall, see the thick, black lines running from bottom to top that illustrate the horizontal velocity component. In Newtonian fluids, the wall shear stress at the separation point is zero.
Currents through pipes and channels
In the case of flows in pipelines and channels , the cross-sectional area A and the tube or channel area W wetted by the fluid are known. Between two locations 1 and 2, the pressure difference and the mean wall shear stress acting on the wall surface must be balanced:
where λ is a loss coefficient related to the coefficient of friction c f and the mean flow velocity. Different approaches for the pressure difference due to the slope of the terrain or for the loss coefficient lead to approximation formulas for the flow velocities ( flow formulas ) or the pressure losses to be expected .
See also
literature
- H. Oertel (ed.): Prandtl guide through fluid mechanics. Fundamentals and phenomena . 13th edition. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5 .
Web links
- Erich Schülein: Optical method for measuring wall shear stress. High speed configuration department. German Aerospace Center (DLR), accessed on January 20, 2016 .