Flow resistance
The flow resistance is the physical quantity that in fluid dynamics describes the force that the fluid as a medium opposes to a movement. A body that moves relative to a gaseous or liquid medium experiences a flow resistance, a force acting in opposition to the relative speed. If an object moves through the air like an airplane , one speaks of air resistance or air friction , see also aerodynamics . Movement in water is called water resistance , see also hydrodynamics .
Forces on bodies in a flow
The flow exerts different shear stress and pressure (normal stress) on the surface of a body in flow. If pressure and shear stress are integrated over the entire surface, one obtains the resulting force that the flow exerts on the body. This force has a certain direction in space. The force component that lies in the direction of the flow direction is the drag force. In addition to the drag force, other force components are the buoyancy force and the side force. Often these forces are measured in the wind tunnel .
In the case of motor vehicles , it is common to specify the force components with reference to a coordinate system that is fixed to the vehicle.
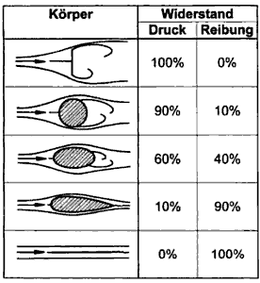
Components of the flow resistance
It is the physical parameters pressure and shear stress that act on the surface of a body and can thus contribute to the flow resistance. Accordingly, the flow resistance can be divided into a pressure resistance and a shear stress resistance . Depending on the shape of the body in flow and the direction of flow, the pressure resistance or the shear stress resistance may predominate.
Depending on the case at hand, it proves to be favorable for the consideration and calculation to treat certain effects that occur when the body flows around the body separately. This is the background for the interference resistance, induced resistances and the wave impedance.
Pressure resistance (form resistance)
The pressure resistance follows from the pressure distribution (normal stress) around a body. The pressure in the separation area at the stern of bodies is lower than that in the stagnation point . The effective area of this resistance is the projected area in the direction of the flow.
Shear stress resistance (frictional resistance, sheet resistance)
The shear stress resistance is the result of friction, i.e. the viscous momentum exchange. It is based on the shear stresses that occur on the surface of the body when the flow sweeps over the surface.
Interference resistance
The interference resistance describes the flow resistance that occurs when previously completely independent flow bodies become flow bodies lying next to one another. It is defined as the difference between the total resistance of the component and the sum of the resistance of the individual components or component groups after assembly. In terms of design, you will always strive for a negative interference resistance. An example is an aircraft fuselage and the aircraft wings before assembly and after assembly. The sum of the individual resistances of the wing and fuselage components is higher than the total resistance after assembly. From a qualitative point of view, the interference resistance is the component of the air force acting against the flow direction on a flow body, which is caused by the mutual influence of the eddies released by different parts of the aircraft or by superimposing the boundary layers in the corners.
Induced resistance
The induced drag is produced whenever an object in a fluid flow generated in the fluid. This is the case, for example, with the generation of lift by the wings of an aircraft, in which, on the one hand, air is accelerated downwards ( downwash ) and, on the other hand , the pressure differences arising from vortex formation ( tip vortex ) are compensated for. The kinetic energy which is then supplied to the air, lost plane.
Wave resistance
The wave resistance occurs with bodies in flow, which move at supersonic or transonic speed . An increase in pressure occurs at body edges that are inclined against the flow, while a decrease in pressure occurs at the edges that are inclined towards the flow. This pressure leads to a force directed against the movement.
Dependence of the flow resistance
The drag force of a body in a certain position depends on the flow velocity , the density and viscosity (tenacity) of the fluid and the geometric dimensions (a characteristic length ) of the body.
This relationship, which comprises five variables, can also be formulated with the aid of a dimensional analysis according to Buckingham's Π theorem using two dimensionless similarity indicators. These similarity measures are the drag coefficient and the Reynolds number , which are defined as
The size is a reference area that must be defined. Usually the face of the body is used as the reference surface, but the wing surface is used for airfoils.
The physical connection can thus be described in the form
The drag force is proportional to the product of the value and the reference area, which is called the drag area. The drag force is obtained from
The factor is called dynamic pressure .
For practical applications, e.g. B. the air resistance of motor vehicles, the dependence on the Reynolds number can often be neglected. Then the value is set as a constant value so that the resistance increases quadratically with the speed. For a comparison of the flow resistance of different vehicles, the drag area is the decisive criterion.
Laminar flow
With laminar flow , the flow resistance is only caused by the internal friction of the medium. Is the dynamic viscosity of the medium, then for spherical body of radius of the Stokes' law
The drag coefficient of a sphere can be determined for the general case of a laminar flow with Reynolds numbers smaller using the following approximation formula:
For Reynolds numbers smaller than 1, Stoke's law applies and the drag coefficient approaches this value !
Turbulent flow
In a turbulent flow , the flow resistance can only be determined through experiments or through complex numerical calculations, e.g. B. by means of finite volume method approximate.
In motor vehicles, but also z. B. cyclists and runners, can be assumed in the relevant speed range of turbulent flow.
In modern automotive engineering, the value, the drag coefficient, is of great importance. In the optimal case it can be 0.07 ( TERA Fennek 2013 ), with the Ford Model T it was 0.9.
literature
- Ernst Götsch: Luftfahrzeugtechnik , Motorbuchverlag, Stuttgart 2003, ISBN 3-613-02006-8
- Thomas Schütz: Hucho - aerodynamics of the automobile . Springer Vieweg, Wiesbaden 2013, ISBN 978-3-8348-2316-8 .
- Willi Bohl, Wolfgang Elmendorf: Technical fluid mechanics . Vogel reference book, Würzburg 2008, ISBN 978-3-8343-3129-8
Web links
- What is Drag : Website of the Glenn Research Center : Flow resistance using the example of an airplane
- Air resistance at student level ( LEIFI )
Individual evidence
- ^ Wolf-Heinrich Hucho: Aerodynamics of the automobile. Definition of the forces and moments acting on a vehicle
- ↑ FLUGTAXI GmbH: PPL% 20Grundbegriffe% 20des% 20Fliegens% 20neutral.pdf PPL Basic concepts of flying , accessed on May 4, 2010.
- ↑ Jürgen Zierep: Similarity laws and model rules of fluid mechanics . Karlsruhe 1991, ISBN 3-7650-2041-9
- ↑ Due to the geometry, the reference area has a fixed ratio to the square of the characteristic length .
- ↑ Wolf-Heinrich Hucho, Syed Rafeeq Ahmed (ed.): Aerodynamics of the automobile: fluid mechanics, heat engineering, driving dynamics, comfort; with 49 tables . Springer-Verlag, 2005, ISBN 3-528-03959-0 , section "Front surface dilemma", p. 276 (1135 p., Limited preview in Google Book search).
- ↑ tec-science: drag coefficient (friction coefficient and pressure coefficient). In: tec-science. May 31, 2020, accessed on June 25, 2020 (German).
- ^ Herbert Sigloch: Technical fluid mechanics . Springer, Berlin, Heidelberg 2007, ISBN 978-3-540-44635-4 , pp. 324 (581 p., Limited preview in Google Book search).
- ↑ Air resistance during cycling training, www.trainingsworld.com, accessed on August 27, 2017