Dimensional analysis

This article was registered in the quality assurance of the physics editorial team . If you are familiar with the topic, you are welcome to participate in the review and possible improvement of the article. The exchange of views about this is currently not taking place on the article discussion page , but on the quality assurance side of physics.

The dimensional analysis is a mathematical process to record the interplay of physical quantities in natural phenomena without knowing the formula on which a physical process is based or an exact law. Their application is based on applied mathematics , practical observation , the execution and evaluation of experiments and an intuitive understanding of physics. It has proven itself particularly in fluid mechanics .

For realistic problems in technology and science, the assigned mathematical equations can in most cases not be solved analytically due to complex boundary conditions , but only numerically, i.e. using computer methods. The application of dimensional analysis to geometrically similar , but laboratory or numerically easier manageable models often allows very precise conclusions to be drawn about the solution of the highly complex initial problem.

The dimensional analysis is mainly used in experimental physics , in engineering , but also in medicine and biology .

application areas

The problems and possible applications are diverse. Some subject areas are:

• Aerodynamics and the behavior of bodies in flowing fluids in general. For example, the investigation and optimization of the aerodynamic properties of aircraft and suspension bridges .
• Flow resistance and pressure reduction in pipes with a flow.
• Formation of waves and their propagation in various media .
• Diffusion and heat transport .
• Explosion processes
• Material strength tests and crash tests .
• The effects of earthquakes (e.g. for high-rise buildings), seepage processes in the ground, the load-bearing capacity of foundations for structures or landslides and avalanches are of geoscientific interest .
• In hydraulic engineering, runoff in channels and bed load transport in rivers.
• In medicine and biology, the subject area of bionics , blood circulation or plant growth.

A dimensional analysis of these processes provides useful proportionalities, specifications for the calibration of model tests (see model laws) and concrete clues for variant studies. Repeatedly, this is sufficient to derive functional relationships from it. In any case, it contributes to a better understanding of the problem.

History and overview

Ludwig Prandtl, one of the fathers of fluid mechanics, and his “hand-operated” flow channel (1904).

Already physicists like Ludwig Prandtl , Theodore von Kármán , Albert Shields , Johann Nikuradse and John William Strutt, 3rd Baron Rayleigh , who at the end of the 19th and beginning of the 20th century were the first to delve deeper into the properties of currents and moving bodies in Fluids , used dimensional analysis to draw conclusions from laboratory experiments with controllable boundary conditions on the behavior of physical problems with geometrically similar bodies or with fluids of different viscosity and density . This similarity principle, i.e. the possibility of being able to examine physical phenomena on different scales, forms the basis of the similarity theory . This theory is often referred to as model theory.

The dimensional analysis on which the similarity theory is based states that every dimension-bound physical formula can be converted into a dimensionless , i.e. H. can be transferred from physical units adjusted form. For this purpose, and are divided by a power product of the variables and at the same time the individual powers are increased: ${\displaystyle y=f(x_{1},x_{2},\dots ,x_{n})}$ ${\displaystyle y}$ ${\displaystyle f(x_{1},x_{2},\dots ,x_{n})}$ ${\displaystyle x_{1},x_{2},\dots }$ ${\displaystyle x_{i}}$

${\displaystyle {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}={\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}},\,k_{i}\in \mathbb {R} \neq 0,}$

so that the left and right sides of the equation become dimensionless. The dimensional purity and thus the correctness of every physical relationship can be checked using this statement. If a formula does not meet these criteria, then it is not physically exact. This applies to many approximation formulas that deliberately neglect certain quantities. It is also clear that only sizes of the same dimension can be added and subtracted, i.e. they can be compared with one another. The arguments of trigonometric or other transcendent functions must therefore be dimensionless numbers.

The important [[ -theorem]], which is based on the dimensional analysis and independently of one another by Aimé Vaschy (1890), Dmitri Pawlowitsch Rjabuschinski (1911) and Edgar Buckingham (1915) , extends the above statement to the effect that the function is in the more general shape ${\displaystyle \Pi }$ ${\displaystyle y=f(x_{1},x_{2},\dots ,x_{n})}$

${\displaystyle {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p}),\,k_{i}\in \mathbb {R} \neq 0}$

can represent. The potency products of , the so-called factors in with , are dimensionless . ${\displaystyle x_{n}}$ ${\displaystyle \Pi }$ ${\displaystyle G}$ ${\displaystyle p<n}$

The dimensional analysis makes it possible to “guess” the functional form of physical formulas down to a real-valued constant , provided that only a few physical quantities have an influence, such as the case law first formulated by Galileo ${\displaystyle C}$

${\displaystyle s(t)=C\cdot g\cdot t^{2}}$

with as the path of fall, as the acceleration of gravity and as the time. The constant of proportionality remains to be determined in the experiment; she surrenders to . ${\displaystyle s}$ ${\displaystyle g}$ ${\displaystyle t}$ ${\displaystyle C}$ ${\displaystyle C=0{,}5}$

Dimensions and systems of measurement

Basic quantities and their units in physics

The concepts of time ...

... or length, illustrated here by the original meter, capture independent dimensions.

Measuring a physical quantity means comparing types of quantities (e.g. speed , pressure ) with something.

For such comparisons one never needs more than seven types of basic sizes, which are called base sizes . Basic units (e.g. meter , second ) are defined for them via prototypes . Each type of base size represents its own dimension that cannot be described using the other types of base size. They are all independent of one another.

→ Main article : "SI base units" in the article International System of Units

Basic size systems

A basic size system includes all dimensions in which a measurement process takes place. A system that contains all known dimensions - L = length , M = mass , T = time , I = current intensity , Θ = thermodynamic temperature , A = amount of substance and J = light intensity - is called {L, M, T, I, Θ , A, J} system. It is sufficient to cover all processes in nature. In mechanics , the main area of ​​application of dimensional analysis, one can usually limit oneself to a {L, M, T} system.

In the basic size system itself, the explicit choice of a basic unit is irrelevant. The length [L] is measured using the basic units of meters , feet , centimeters , yards, etc. The base unit is only used for comparison purposes, it should not be confused with the dimension.

Basic size systems can be formed not only from those basic size types that are also basic size types at the same time, but also with all others. Thus, according to Newton, the force as a combined quantity of mass and the basic quantities length and time is suitable to replace the mass in a {L, M, T} system. Then a {L, F, T} system arises with the basic type of force [F] instead of the mass by which it is defined. As a dimension concept, force has its own, independent dimension , which includes the mass concept.

Equivalence of systems of basic quantities

All types of sizes of a {M, L, T} system can also be specified in a {F, L, T} system. A {M, F, L, T} -system can not exist because of the dependence on mass and force . The demand for mutually independent dimensions would be violated.

Alternatively, one can choose basic variable systems in which the pressure , the speed or the frequency are basic variables. The condition is that each basic quantity represents a dimension independent of the other basic quantities used.

All systems of basic quantities in which the same quantities can be represented are called equivalent . The explicit choice of basic variables is irrelevant for finding so-called Π-factors. It's just a matter of your preferred presentation.

In the mechanics common size species in an {M, L, T} system are listed below, with their dimension formulas. Your units are the power products of the base units. Your dimensional formulas are power products of the dimensions within which these units are described.

Types of sizes commonly used in mechanics in a {M, L, T} system

Size type	Size designation ( formula symbol )	unit	Dimensional formula
Dimensions	${\displaystyle m}$	kg	${\displaystyle M}$
length	${\displaystyle l}$, , , ... ${\displaystyle b}$ ${\displaystyle h}$	m	${\displaystyle L}$
time	${\displaystyle t}$	s	${\displaystyle T}$
frequency	${\displaystyle f}$	Hz (= 1 / s)	${\displaystyle T^{-1}}$
Angular velocity	${\displaystyle \omega }$	1 / s	${\displaystyle T^{-1}}$
speed	${\displaystyle v}$	m / s	${\displaystyle L\cdot T^{-1}}$
acceleration	${\displaystyle a}$	m / s²	${\displaystyle L\cdot T^{-2}}$
pulse	${\displaystyle p}$	m kg / s	${\displaystyle M\cdot L\cdot T^{-1}}$
density	${\displaystyle \rho }$	kg / m³	${\displaystyle M\cdot L^{-3}}$
force	${\displaystyle F}$	N (= kg · m / s²)	${\displaystyle M\cdot L\cdot T^{-2}}$
Weights	${\displaystyle \gamma }$	N / m³	${\displaystyle M\cdot L^{-2}\cdot T^{-2}}$
Pressure , tension	${\displaystyle p}$	N / m²	${\displaystyle M\cdot L^{-1}\cdot T^{-2}}$
modulus of elasticity	${\displaystyle E}$	N / m²	${\displaystyle M\cdot L^{-1}\cdot T^{-2}}$
energy	${\displaystyle W}$	J (= m² kg / s²)	${\displaystyle M\cdot L^{2}\cdot T^{-2}}$
power	${\displaystyle P}$	W (= m² kg / s³)	${\displaystyle M\cdot L^{2}\cdot T^{-3}}$
Dynamic viscosity	${\displaystyle \mu }$	N · s / m²	${\displaystyle M\cdot L^{-1}\cdot T^{-1}}$
Kinematic viscosity	${\displaystyle \nu }$	m² / s	${\displaystyle L^{2}\cdot T^{-1}}$

Formulations such as “decisive quantity of density” or “influence of the quantities speed and acceleration” are colloquial. This use of the term size is incorrect in the physical sense. Density , speed , acceleration , etc. are types of sizes. Only in an equation of the kind:

${\displaystyle v=3\,\mathrm {m/s} }$

a quantity (one can also speak of a measured quantity ) is described via a (measure) unit [m / s] and a measure 3. However, this is not relevant for technical purposes. ${\displaystyle v}$

Basic quantity systems and their transformations

Every basic quantity system can be converted into an equivalent one with the help of a transition matrix, which contains the exponents of the dimensions. For example, if you want the dimension of force in a basic system of quantities, given in the form ${\displaystyle F}$

${\displaystyle F^{1}=M^{1}\cdot L^{1}\cdot T^{-2}}$,

express by the mass , this is achieved by the simple algebraic conversion ${\displaystyle M}$

${\displaystyle M^{1}=F^{1}\cdot L^{-1}\cdot T^{2}}$.

Or, presented in a clear form, with the transition matrix of the exponents ${\displaystyle D_{1}}$

${\displaystyle D_{1}={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\\mathbf {M} &1&-1&2\\\mathbf {L} &0&1&0\\\mathbf {T} &0&0&1\\\end{pmatrix}}}$

The transformation of the basic quantities of the {M, L, T} system to the {F, L, T} basic quantity system is through the matrix multiplication

${\displaystyle R\cdot D_{1}={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\m&1&0&0\\l,b,h,\dots &0&1&0\\t&0&0&1\\f&0&0&-1\\\omega &0&0&-1\\v&0&1&-1\\a&0&1&-2\\\rho &1&-3&0\\F&1&1&-2\\\gamma &1&-2&-2\\p,E&1&-1&-2\\W&1&2&-2\\P&1&2&-3\\\mu &1&-1&-1\\\nu &0&2&-1\\\end{pmatrix}}\cdot {\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\\mathbf {M} &1&-1&2\\\mathbf {L} &0&1&0\\\mathbf {T} &0&0&1\\\end{pmatrix}}={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\m&1&-1&2\\l,b,h,\dots &0&1&0\\t&0&0&1\\f&0&0&-1\\\omega &0&0&-1\\v&0&1&-1\\a&0&1&-2\\\rho &1&-4&2\\F&1&0&0\\\gamma &1&-3&0\\p,E&1&-2&0\\W&1&1&0\\P&1&1&-1\\\mu &1&-2&1\\\nu &0&2&-1\\\end{pmatrix}}=Q}$.

possible if the dimensional matrix contains the exponents of all dimensional formulas of the {M, L, T} system. The desired exponents of the dimensional formulas in the {F, L, T} system can then be found in the dimensional matrix . ${\displaystyle R}$ ${\displaystyle Q}$

Since length and time remain unaffected by the transformation, only the exponents of those quantities that are correlated with the dimension of mass change . It can be seen that the dimensional formulas are simplified for some basic variables, such as pressure . For others, however, such as the density , which is directly dependent on mass , complicates it. It is useful to create such a basic size system in which the sizes of the specific problem can be represented as simply as possible. ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle \rho }$

Π factors

definition

${\displaystyle \Pi }$-Factors are those products that result from a matrix like the dimensional matrix above , when individual quantities are raised to arbitrary powers and multiplied by other quantities occurring in the matrix in such a way that the product becomes dimensionless or has dimension 1. The dimension of a quantity is indicated by the bracket symbol . For example, the potency product is ${\displaystyle R}$ ${\displaystyle x}$ ${\displaystyle [x]}$

${\displaystyle \Pi =v^{1}\cdot a^{-1}\cdot t^{-1}}$

a factor of the matrix that has the required dimension ${\displaystyle \Pi }$ ${\displaystyle R}$

${\displaystyle [\Pi ]=L^{1}\cdot T^{-1}\cdot L^{-1}\cdot T^{2}\cdot T^{-1}=1}$

owns. The dimension 1 is of course retained even if one raises to arbitrary powers. It is: ${\displaystyle \Pi }$

${\displaystyle [\Pi ^{2}]=[{\sqrt {\Pi }}]=[\Pi ^{\lambda }]=1,\,\lambda \in \mathbb {R} \neq 0}$

Number of Π factors

Any number of representations of a factor that has been found are possible. The number of -factors, which cannot be written as the power of a previously found factor or as the product of factors raised in powers, is limited . About the existence of these factors in a chosen dimensional matrix it can be said that there are precisely linearly independent factors. ${\displaystyle \Pi }$ ${\displaystyle \Pi }$ ${\displaystyle A}$ ${\displaystyle p=n-r}$ ${\displaystyle \Pi }$

There are:

• p: The number of dimensionless factors ${\displaystyle \Pi }$
• n: The number of dimensional quantities
• r: the rank of the matrix . ${\displaystyle A}$

Formal procedure for a dimensional analysis

${\displaystyle A}$is to be selected as a dimension matrix with rows for the sizes and 3 columns for 3 dimensions : ${\displaystyle n}$ ${\displaystyle x_{n}}$ ${\displaystyle Y_{j}}$

${\displaystyle (1)\quad A={\begin{pmatrix}&Y_{1}&Y_{2}&Y_{3}\\x_{1}&a_{11}&a_{12}&a_{13}\\x_{2}&a_{21}&\ddots &\ddots \\x_{3}&a_{31}&\ddots &\ddots \\\vdots &\ddots &\ddots &\vdots \\x_{n}&a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}}$

If one finds a row vector with the number of columns , for which applies: ${\displaystyle k}$ ${\displaystyle n}$

${\displaystyle (2)\quad k\cdot A={\begin{pmatrix}k_{1}&k_{2}&k_{3}&\dots &k_{n}\end{pmatrix}}\cdot {\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&\ddots &\vdots \\a_{31}&\ddots &\vdots \\\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}={\begin{pmatrix}0&0&0\\\end{pmatrix}}}$

then you have:

${\displaystyle (3)\quad \Pi =x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}$

found a factor of . ${\displaystyle \Pi }$ ${\displaystyle A}$

Control options

The number of linearly independent row vectors that satisfy this equation (2) is . One proves their linear independence by showing that the rank of the matrix that can be built from found row vectors is also . ${\displaystyle p}$ ${\displaystyle K}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle (4)\quad \mathrm {rg} (K)={\begin{pmatrix}k_{11}&k_{12}&k_{13}&\dots &k_{1n}\\\vdots &\vdots &\vdots &\vdots &\vdots \\k_{p1}&k_{p2}&k_{p3}&\dots &k_{pn}\\\end{pmatrix}}=p}$

Multiplied by the result is the zero matrix with the number of dimensions selected (here: 3) as columns and the number of vectors as rows. ${\displaystyle K}$ ${\displaystyle A}$ ${\displaystyle 0}$

${\displaystyle (5)\quad {\begin{pmatrix}k_{11}&k_{12}&k_{13}&\dots &k_{1n}\\\vdots &\vdots &\vdots &\vdots &\vdots \\k_{p1}&k_{p2}&k_{p3}&\dots &k_{pn}\\\end{pmatrix}}\cdot {\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&\ddots &\vdots \\a_{31}&\ddots &\vdots \\\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}\\\end{pmatrix}}={\begin{pmatrix}0&0&0\\\vdots &\vdots &\vdots \\0&0&0\\\end{pmatrix}}}$

The matrix algebra shows that any linear combination of the row vectors found solves equation (2) and thus represents a factor. Accordingly, (5) is also fulfilled for every matrix that results from by multiplying rows with any real numbers other than zero and adding or subtracting them with other rows. Nothing changes in the rank of the matrix . For the number of possible possible solutions, this means that you can use the found -factors to create any number of other -factors: ${\displaystyle \Pi }$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle p}$ ${\displaystyle \Pi }$ ${\displaystyle \Pi }$

${\displaystyle (6)\quad \Pi =\Pi _{1}^{\lambda _{1}}\cdot \Pi _{2}^{\lambda _{2}}\cdot \quad \cdot \Pi _{p}^{\lambda _{p}},\,\lambda _{i}\in \mathbb {R} \neq 0,}$

where their associated row vectors would be homogeneous solutions of (2). However, there are still only exact factors that form a fundamental system of the dimensional matrix. ${\displaystyle p}$ ${\displaystyle \Pi }$

Conclusions

• With any fundamental system , all existing solutions of (2) are determined via (6). Any number of solutions can be displayed.
• Dimensionless number constants, which are often ratios, remain dimensionless in this calculation and automatically represent a dimensionless Π-factor.

Finding a fundamental system of Π-factors

Analytical approach

A first possibility to obtain a fundamental system of -factors is to let the independent variables in the equation system, which results from (2) assume any values ​​other than zero, and to check the rank of the row matrix according to (4). The number of independent variables is identical to the number of factors. ${\displaystyle \Pi }$ ${\displaystyle k_{i}}$ ${\displaystyle \Pi }$

In the system of equations, those variables that can be assigned any number of values ​​without causing a contradiction in the solution are independent or freely selectable . For example, a smart choice is always to assign the numerical value one to an independent variable and to set the other independent variables to zero. The missing dependent variables result from the solution of the remaining system of equations.

The disadvantage of this method, however, is that you have very little influence on the appearance of this fundamental system and you may have to solve a large number of systems of equations.

Method of guessing

A more useful method is to simply guess individual factors from (1). To do this, you have to add the lines of the sizes in the dimension matrix "to zero". ${\displaystyle \Pi }$ ${\displaystyle A}$

In practice this means:

• If you want a quantity in the counter , you have to multiply its line by “+1”, otherwise by “−1”. (Multiplying the lines by numbers means raising the sizes to the corresponding powers.)
• If the addition of such rows results in zero, one has a power product (as demonstrated previously with the matrix ). ${\displaystyle S}$

This method includes the ability to influence the appearance of factors. However, one has to confirm the rank of the resulting row matrix afterwards, for example by finding a non-vanishing sub-determinant, i.e. showing that (4) is satisfied. ${\displaystyle \Pi }$

Evaluation of the methods

Usually, guessing the factors with a skilful choice of the basic size system and clear relationships leads to the goal much faster than a formal procedure.

In the literature on linear algebra , further methods for the analytical finding of the -factors are demonstrated in order to solve the system of equations from (2) as skilfully as possible, e.g. B. the Gaussian elimination method . ${\displaystyle \Pi }$

Formation of physically useful fundamental systems

If one has arrived at a fundamental system, this often does not satisfy the desire for a physical meaningfulness of the individual factors. The application of equation (6) provides a remedy. ${\displaystyle \Pi }$

By cleverly combining the factors with one another and raising them to arbitrary powers, a new, physically more productive factor can easily be formed. If this is to be present in a new fundamental system, only one of the factors has to be deleted by the combination of which one had formed the new one. This makes the newly acquired factor linearly independent of the rest. Assume that there is a fundamental system with as -factors, and a new, more meaningful factor, the shape ${\displaystyle \Pi }$ ${\displaystyle \Pi _{1},\Pi _{2},\Pi _{3}}$ ${\displaystyle \Pi }$

${\displaystyle \Pi _{4}=\Pi _{1}^{-1}\cdot \Pi _{2}^{2}}$

then there would be a new fundamental system or , but not , since it depends linearly on the first two. ${\displaystyle \Pi _{1},\Pi _{3},\Pi _{4}}$ ${\displaystyle \Pi _{2},\Pi _{3},\Pi _{4}}$ ${\displaystyle \Pi _{1},\Pi _{2},\Pi _{4}}$ ${\displaystyle \Pi _{4}}$

For model investigations it is useful to have formed such factors that always contain a characteristic quantity that then only occurs in a single factor. This does not necessarily have to be possible. Equation (6) allows this to be checked.

Dimensionally homogeneous functions

If there is a dimensionally homogeneous function with a dimension-bound function value that is determined by quantities , then ${\displaystyle y}$ ${\displaystyle x_{i}}$

${\displaystyle (7)\quad y=f(x_{1},x_{2},\dots ,x_{n});\,\,[y]=[f(x_{1},x_{2},\dots ,x_{n})]\neq 1}$

then there is always a potency product such that it can be written:

${\displaystyle (8)\quad {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}={\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}},\,k_{i}\in \mathbb {R} \neq 0}$

${\displaystyle \left[{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right]=\left[{\frac {f(x_{1},x_{2},\dots ,x_{n})}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right]=1}$

Every physical formula and in particular its function value bound to a unit can be represented dimensionlessly by raising the power of the quantities contained in the function . ${\displaystyle y}$ ${\displaystyle f}$ ${\displaystyle x_{i}}$

Statements of the Π-theorem

The so-called -theorem (also often Buckingham theorem in literature ) leads one step further. Its main message is that every dimensional equation ${\displaystyle \Pi }$

${\displaystyle y=f(x_{1},x_{2},\dots ,x_{n});\quad [y]=[f(x_{1},x_{2},\dots ,x_{n})]\neq 1}$

in the form of

${\displaystyle (9)\quad {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})}$

${\displaystyle \left[{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}\right]=\left[G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})\right]=1,\,k_{i}\in \mathbb {R} \neq 0,\,p\,{\text{wie vorher}}}$

can be converted and is thus built up only from dimensionless power products (and number constants). It may be that there are several ways to represent the left side of the equation in dimensionless form. Occasionally the left side is also referred to as the Π factor in the literature. This is legitimate, but not consistent, because the separation into the left and right side gives a more precise statement

${\displaystyle {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}-G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p})=0}$

instead of

${\displaystyle F\left(\Pi _{1},\Pi _{2},\dots ,\Pi _{p},{\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \dots \cdot x_{n}^{k_{n}}}}\right)=0}$

The importance of the theorem lies in the fact that a statement can be made about the functional relationship between dimensional physical quantities that may not be explicitly stated in a formula. This applies to many complex issues in nature (e.g. turbulence , Kármán vortex street ). Since quantities can only occur in certain relationships, the Π-factors presented, at the same time a useful reduction of the function variables in compared to those in is achieved , because it applies again . ${\displaystyle G}$ ${\displaystyle f}$ ${\displaystyle p=n-r}$

Conclusions

If the number of Π-factors is clear, then: ${\displaystyle p}$

• At , the functional relationship sought is determined except for a proportionality constant. ${\displaystyle p=0}$
• If one or more factors ( ) exist , a functional relationship can only be guessed at, e.g. from experimental results or pure intuition. It cannot be derived explicitly. ${\displaystyle p>0}$

Often in the second case, the Rayleigh product approach applies, i.e. the Π-factors found, multiplied with one another and increased to a corresponding, often whole-number power, deliver the end result sought.

Two more general conclusions can be drawn:

• Theorem 1: If a quantity is not needed to arrive at a fundamental system of Π-factors or to make it dimensionless, then either does not depend on, or the imaginary functional relationship must be expanded by at least one further quantity. ${\displaystyle x_{a}}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x_{a}}$
• Theorem 2: If no power product can be made dimensionless from the , then the dimension matrix is ​​incomplete or wrong. ${\displaystyle y}$ ${\displaystyle x_{i}}$

This means that in any case with dimensional equations, which physical formulas always are, one can arrive at an advantageous, dimensionless representation in which the units of the quantities play no role.

These fundamental principles are important for all of physics.

Vectors and tensors

Dimensional analysis reaches its limits when not only scalar quantities such as pressure or temperature or one-dimensional, straight movement processes are dealt with, but vectors and tensors come into play.

Since only one physical dimension of length is available, but a three-dimensional Cartesian coordinate system is required for the description of spatial processes (where vectors come into play), for the two-dimensional parabolic flight of a cannonball, for example, its time-dependent height and width would have to be examined separately. This does not exclude that one can derive a valid equation for the flight within a right-angled and immobile coordinate system by knowing the symmetries in both formulas and the necessary background knowledge . If the sphere is also deflected by a cross wind, and the problem is three-dimensional, the complexity to be recorded increases further.

The apparent contradiction between the three dimensions of space and the one available dimension of length dissolves when one mentally aligns this length dimension to the flight curve itself in a moving coordinate system. If you follow the path, the curve and the ball speed are one-dimensional. The dimensional analysis is therefore entirely valid. The path speed along the curve can be recorded one-dimensionally, namely via the amount of the speed vector. This is only of little help to an immobile observer who not only wants to gain knowledge about the magnitude of the speed or the distance covered by the ball, but also about the direction of the speed and the ball's position in space.

The same applies to three-dimensional stress states (e.g. when examining material strengths), which would have to be recorded with a stress tensor .

Transition to model theory

The third important conclusion that makes the theorem meaningful in experimental experimental technique is that: ${\displaystyle \Pi }$

Similarity of air vortices on a small scale ...

... and on a large scale with Hurricane Fran .

• Theorem 3: If in the dimensionless function equation

${\displaystyle {\frac {y}{x_{1}^{k_{1}}\cdot x_{2}^{k_{2}}\cdot \ldots \cdot x_{n}^{k_{n}}}}=G(\Pi _{1},\Pi _{2},\dots ,\Pi _{p}),\,k_{i}\in \mathbb {R} \neq 0}$ all factors on the right side of the equation are kept constant, then the dimensionless function result on the left side will always be the same. ${\displaystyle \Pi }$

Theorem 3 is crucial for the entire theory of similarity . All of the boundary conditions to be selected in realistic model tests emerge from this (see complete and partial model similarity ).

The Reynolds number is an example of a Π factor that is important in model experiments . This is:

${\displaystyle Re={\frac {\rho \cdot v\cdot L}{\mu }}={\frac {v\cdot L}{\nu }}}$ With: ${\displaystyle \mu =\nu \cdot \rho }$

Since a geometric length , the flow velocity, the density and the viscosity are included in the Reynolds number , it is possible to examine scaled smaller models (e.g. aircraft in a flow channel) and still obtain a correct result on the left-hand side of the dimensionless function equation above by examining the model and / or making adjustments. ${\displaystyle L}$ ${\displaystyle v}$ ${\displaystyle \rho }$ ${\displaystyle \mu }$ ${\displaystyle v}$ ${\displaystyle \nu }$

The same characteristic Π-factors occur repeatedly in many problems. Many of them are named after their discoverers and researchers under the heading of dimensionless index .

Full and partial model similarity

If it is possible to keep all Π-factors constant in a physically interesting range of values, one speaks of complete model similarity , otherwise of partial model similarity .

Often, however, the complete model similarity does not succeed, and one is forced to estimate the more or less large side effect on the final measurement result. Side effects can also occur in other ways, namely if a variable, whose influence on the prototype would be insignificant, has an undesirably strong influence on the model (see Froude number in the ship model ).

Cavitation in a propeller in a scale model test. The constancy of Reynolds numbers in the model and prototype requires four times the speed of rotation of the model propeller when its diameter is halved.

Model laws

The equation of the Π-factors of model and prototype results in model laws . If you vary the length in the Reynolds number of the model compared to the prototype, you can, as explained above, compensate for this by adjusting the viscosity and / or the speed.

In order to bring the model laws into an advantageous form, one always endeavors to include only those quantities in the Π-factors that can also be varied in the model and not those that would result from the consequence of this variation. The most practical form is achieved when it is possible to write these equations in such a way that when inserting the size values ​​of the prototype, a clear statement about an individual test setting in the model is always possible. In other words, in such a way that with every change in the initial situation in the prototype, the required test setting is always revealed in the model.

Model tests

Another advantage that should not be underestimated is that you no longer have to vary all of the influencing variables individually in a model test, but only the Π-factors that are formed from them and that are smaller in number. This is also of decisive importance for the presentation of the later test results. By only applying Π-factors instead of individual, dimensionally-dependent quantities, one arrives at a much tighter and clearer illustration of the measured quantities (one saves dimensions). All diagrams in which the axes are shown without dimensions are based on the dimensional analysis.

When building a model and later carrying out the test, one must carefully consider all the relevant parameters in advance. The correct or a complete set of Π-factors and a realistic simulation can only be obtained with the correct parameters. If too many variables are selected, which may have little impact on the measurement , the number of attempts increases enormously. This requires physical expertise.

Perhaps, in retrospect, it turns out that a variable that has been assigned a meaning has far less influence on the result than assumed. If this size only occurs in a single factor, it is possible to delete this. Otherwise it is advisable to form the dimensional matrix with a new set of sizes and to find a suitable fundamental system.

Examples

To demonstrate the use of the formulas from the previous chapters, some calculation examples follow.

Galileo's Fall Law

First, it is mistakenly assumed that in the case law of Galileo Galilei the falling path next to the acceleration due to gravity and time and from the mass depended on the falling body, thus: ${\displaystyle s}$ ${\displaystyle g}$ ${\displaystyle t}$ ${\displaystyle m}$

${\displaystyle s=f(g,t,m)\,}$

The assigned dimension matrix is in full notation ${\displaystyle A}$

${\displaystyle A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\g&0&1&-2\\t&0&0&1\\m&1&0&0\\\end{pmatrix}}}$

or in a mathematically exact formulation

${\displaystyle A={\begin{pmatrix}0&1&-2\\0&0&1\\1&0&0\end{pmatrix}}.}$

Since all row vectors are independent of linear, the rank is given by ; there are no Π-factors, because with applies . It can only apply: ${\displaystyle A}$ ${\displaystyle \mathrm {rg} (A)=3}$ ${\displaystyle n=r=3}$ ${\displaystyle p=n-r=0}$

${\displaystyle {\frac {s}{gt^{2}}}={\text{const.}}}$

The approach cannot be made dimensionless and is therefore physically incorrect. A dependency of the fall distance on the mass only leads to a correct description if the air is taken into account. Because the air density responsible for the braking friction contains the dimension of mass. ${\displaystyle s=f(g,t,m)}$

The differential calculus was not available to Galileo . He did not know that the speed of fall is the time derivative of the path of fall . At times he assumed that . If he had used dimensional analysis, it would have been clear that the approach to ${\displaystyle v}$ ${\displaystyle s}$ ${\displaystyle s\sim v}$ ${\displaystyle s=f(v,g)}$

${\displaystyle {\frac {sg}{v^{2}}}={\text{const.}}}$

leads and this without knowledge of differential calculus.

Euler's kink rod

Vertically loaded bars of a certain length are at risk of buckling , i.e. H. their failure often occurs before the actual breaking load of the cross-section is reached. The so-called buckling load of such a bar with a rectangular cross-section depends on the modulus of elasticity , its length , its cross-sectional height , its cross- sectional thickness and the storage conditions at the ends: ${\displaystyle F}$ ${\displaystyle E}$ ${\displaystyle l}$ ${\displaystyle h}$ ${\displaystyle d}$

${\displaystyle F=f(E,l,h,d)\,}$.

The 4 Euler cases with the following boundary conditions (from left to right): (1) restrained / free, (2) articulated / articulated, (3) restrained / articulated, (4) restrained / restrained

The dimensional matrix for the second case in the figure on the right results for a {F, L, T} system in detailed notation ${\displaystyle A}$

${\displaystyle A={\begin{pmatrix}&\mathbf {F} &\mathbf {L} &\mathbf {T} \\E&1&-2&0\\l&0&1&0\\h&0&1&0\\d&0&1&0\\\end{pmatrix}}}$

or in a mathematically exact formulation

${\displaystyle A={\begin{pmatrix}1&-2&0\\0&1&0\\0&1&0\\0&1&0\\\end{pmatrix}}}$.

The rank of is . The number of Π-factors results from and to . These two easy-to-guess Π-factors are the so-called geometric similarities and . For dimensionless must ${\displaystyle A}$ ${\displaystyle r:=\mathrm {rg} (A)=2}$ ${\displaystyle n=4}$ ${\displaystyle r=2}$ ${\displaystyle p=n-r=2}$ ${\displaystyle \Pi _{1}=hl^{-1}}$ ${\displaystyle \Pi _{2}=hd^{-1}}$ ${\displaystyle F}$

${\displaystyle {\frac {F}{E\cdot l^{2}}}=G\left({\frac {h}{l}},{\frac {h}{d}}\right)}$

apply, with which the dimensional analysis has shown that one only has to vary the so-called slenderness of the rod and the aspect ratio of the cross-section in laboratory tests in order to obtain the buckling load for any modulus of elasticity of rectangular rods. ${\displaystyle hl^{-1}}$ ${\displaystyle hd^{-1}}$

According to equation 6 in the section Existence and number of Π-factors , another Π-factor can be formed:

${\displaystyle \Pi _{3}=\Pi _{1}\cdot \Pi _{2}^{-1}={\frac {h}{l}}\cdot {\frac {1}{\frac {h}{d}}}={\frac {d}{l}}}$.

With the help of this factor, dimensional analysis provides the equivalent relationship

${\displaystyle {\frac {F}{E\cdot l^{2}}}=G\left({\frac {h}{l}},{\frac {d}{l}}\right)}$.

It often makes sense to use the Π-factors as a product. This leads to the equation for this example ${\displaystyle G}$

${\displaystyle {\frac {F}{E\cdot l^{2}}}=C\cdot \left({\frac {h}{l}}\right)^{3}\cdot {\frac {d}{l}}}$,

that of the exact relationship established by Leonhard Euler

${\displaystyle F={\frac {\pi ^{2}}{12}}\cdot {\frac {E\cdot h^{3}\cdot d}{l^{2}}}}$

analog, d. H. is of the same functional form. The buckling load can be easily verified in tests on bars of any length and elasticity, and not just limited to the rectangular shape, and shown in diagram form. Knowledge of closed formulas, such as Euler's, is not necessary. What is remarkable is the knowledge gained that the modulus of elasticity and length of a fixed cross-section for a buckling test can in principle be freely selected. The proportionality between , and is known from dimensional analysis. ${\displaystyle F}$ ${\displaystyle E}$ ${\displaystyle l}$

Bodies flowing around in fluids

Flow resistance of a sphere

The standard problem in the early days of fluid mechanics was the determination of the resistance of a body in a fluid . This can be recorded with the help of the dimensional analysis.

The resistance of a sphere and any other body depends on its shape, here specified by the diameter of the sphere , the speed with which it moves in the fluid, the density of the medium and its dynamic viscosity . ${\displaystyle F}$ ${\displaystyle d}$ ${\displaystyle v}$ ${\displaystyle \rho }$ ${\displaystyle \mu }$

Drag coefficient of a sphere as a function of the Reynolds number . For small Re and thus low speeds, the Stokes law applies. The representation is dimensionless.

The functional connection is sought . ${\displaystyle F=f(v,\rho ,\mu ,d)}$

The dimensional matrix in a {M, L, T} system is: ${\displaystyle A}$

${\displaystyle A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\v&0&1&-1\\\rho &1&-3&0\\\mu &1&-1&-1\\d&0&1&0\\\end{pmatrix}}\,{\text{bzw.}}\,A={\begin{pmatrix}0&1&-1\\1&-3&0\\1&-1&-1\\0&1&0\\\end{pmatrix}}}$

The rank of is 3. There is Π-factor, the famous Reynolds number , named after the person who recognized this principle, Osborne Reynolds, and thus: ${\displaystyle A}$ ${\displaystyle p=n-r=4-3=1}$

${\displaystyle {\frac {F}{\rho \cdot v^{2}\cdot d^{2}}}=G\left({\frac {v\cdot d\cdot \rho }{\mu }}\right)=G(Re)}$

For is usually reformulated with number constants that appear reasonable , whereby the convention is that the face of the body is replaced and the proportionality factor 1/2 from the dynamic pressure is added. The connection also applies to this reformulation ${\displaystyle G(Re)}$ ${\displaystyle C_{D}}$ ${\displaystyle d^{2}}$ ${\displaystyle C_{D}=C_{D}(Re)}$

The resistance you are looking for is:

${\displaystyle F=C_{D}\cdot {\frac {1}{2}}\rho v^{2}\cdot {\frac {d^{2}\pi }{4}}}$

${\displaystyle C_{D}}$is called the drag coefficient . It can be determined through experiments and, as can be seen in the dimensionless diagram, is speed-dependent and in no way constant. The relationship between and determined by measurements can be used to convert to spheres with a different diameter d and other fluids. ${\displaystyle C_{D}}$ ${\displaystyle Re}$

At the beginning at low , the analytically difficult to derive linear Stokes law applies . Then, at higher speeds, it varies , due to the formation of eddies on the back of the ball. Similar diagrams can be determined with experiments for any geometric shapes and bodies. ${\displaystyle Re}$ ${\displaystyle C_{D}}$

Models of ships

Sketch ship model

Pilot of an F-18 - Jets in the water. Since the density of water is around 800 times that of air, but the viscosity is only by a factor of around 100, even small models achieve the same Reynolds numbers as airplanes at low flow velocities and enable realistic ones with limited effort Simulations.

A ship is examined as a model on a small scale 1: 100.

The prototype, i.e. the real ship, has the length and breadth . Its draft is and it goes with speed . The water possesses the density and the dynamic tenacity . The process is subject to the acceleration of gravity , because waves subject to the law of gravity arise on the surface of the water . The water is sufficiently deep opposite . ${\displaystyle L}$ ${\displaystyle D}$ ${\displaystyle t}$ ${\displaystyle v}$ ${\displaystyle \rho }$ ${\displaystyle \mu }$ ${\displaystyle g}$ ${\displaystyle t}$

The flow resistance in the direction of travel, measured by a force , is examined . Only independent variables may be included in the dimension matrix. Since the weight is, for example , only two of these three variables are permitted as input variables. ${\displaystyle F}$ ${\displaystyle \gamma =\rho \cdot g}$ ${\displaystyle A}$

The functional connection is sought ${\displaystyle F=f(v,g,\rho ,\mu ,L,D,t)}$

The dimensional matrix in a {M, L, T} system is presented as: ${\displaystyle A}$

${\displaystyle A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\v&0&1&-1\\g&0&1&-2\\\rho &1&-3&0\\\mu &1&-1&-1\\L&0&1&0\\D&0&1&0\\t&0&1&0\\\end{pmatrix}}\,\,{\text{bzw.}}\,A={\begin{pmatrix}0&1&-1\\0&1&-2\\1&-3&0\\1&-1&-1\\0&1&0\\0&1&0\\0&1&0\\\end{pmatrix}}}$

The rank of is 3. The following applies for the number of Π-factors . With experience in fluid mechanics you can guess: ${\displaystyle A}$ ${\displaystyle p}$ ${\displaystyle p=n-r=7-3=4}$

${\displaystyle \Pi _{1}={\frac {L}{D}}\,}$, , , ${\displaystyle \Pi _{2}={\frac {t}{D}}\,}$ ${\displaystyle \Pi _{3}=Re={\frac {\rho \cdot v\cdot D}{\mu }}\,}$ ${\displaystyle \Pi _{4}=Fr={\frac {v^{2}}{g\cdot D}}}$

${\displaystyle \Pi _{1}}$and are geometric similarities. True-to-scale curves of the ship shape are assumed. is the Reynolds number and the Froude number . ${\displaystyle \Pi _{2}}$ ${\displaystyle \Pi _{3}}$ ${\displaystyle \Pi _{4}}$

The dimensionless relationship

${\displaystyle {\frac {F}{g\cdot \rho \cdot L\cdot D\cdot t}}=G\left({\frac {L}{D}},{\frac {t}{D}},Re={\frac {\rho \cdot v\cdot D}{\mu }},Fr={\frac {v^{2}}{g\cdot D}}\right)}$

is valid.

Complete model similarity is achieved when all Π-factors in the model and prototype can be kept constant. With and this is trivial. Remain in the water and unchanged. The constancy of the Reynolds number requires the speed to be increased by the scale factor 100, since it was reduced by 100. ${\displaystyle \Pi _{1}}$ ${\displaystyle \Pi _{2}}$ ${\displaystyle \rho }$ ${\displaystyle \mu }$ ${\displaystyle Re}$ ${\displaystyle v}$ ${\displaystyle D}$

• Dilemma: The Froude number is based on the square of the speed . For the constancy of , the acceleration due to gravity would have to be adapted, which can not be achieved without a centrifuge on earth. Complete model similarity cannot be achieved, only or can be constant. Alternatively, the model can be examined in another liquid with a corresponding density and viscosity . ${\displaystyle Fr}$ ${\displaystyle v}$ ${\displaystyle Fr}$ ${\displaystyle g}$ ${\displaystyle Re}$ ${\displaystyle Fr}$
• Conclusion: Plays both as well as a role will not achieve full model similarity rule. Very small models also require high flow velocities. Many models are therefore only realistic if they are correspondingly large. ${\displaystyle Fr}$ ${\displaystyle Re}$

Models of airplanes and submarines

For flow processes in which the free surface of the fluid does not play a role, the Froude number is not relevant due to the lack of surface wave formation. Models of submarines or aircraft (below the speed of sound ) can in principle be examined if they are completely similar. Only the Reynolds number is decisive.

In order to avoid huge, unrealizable flow speeds in the wind tunnel, aircraft models are often flown against in denser media. When an object is moving so fast that the compression modulus of the fluid matters, the Mach number comes into play. Then the relationship applies . and are characteristic dimensions. The result are three already known and one new Π-factor: ${\displaystyle K}$ ${\displaystyle {\mathit {Ma}}}$ ${\displaystyle F=f(v,\rho ,\mu ,K,L,D,T)}$ ${\displaystyle L}$ ${\displaystyle D}$

${\displaystyle \Pi _{1}={\frac {L}{D}}\,}$, , , ${\displaystyle \Pi _{2}={\frac {t}{D}}\,}$ ${\displaystyle \Pi _{3}=Re={\frac {\rho \cdot v\cdot D}{\mu }}\,}$ ${\displaystyle \Pi _{4}={\mathit {Ma}}={\frac {v}{\sqrt {\frac {K}{\rho }}}}}$

The denominator of is the speed of longitudinal waves in elastic media, in air the so-called speed of sound . The Mach number is of influence from values ​​of around . is strongly pressure and temperature dependent in gases. ${\displaystyle {\mathit {Ma}}}$ ${\displaystyle {\mathit {Ma}}=0{,}8}$ ${\displaystyle K}$

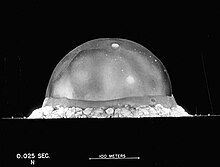
Energy of the first atomic bomb test in New Mexico in 1945

A famous example of the application of dimensional analysis comes from the British physicist Geoffrey Ingram Taylor . After receiving a series of images with precise time intervals of the first atomic bomb explosion in New Mexico in 1945 ( Trinity test ), he was able to determine the energy released by the nuclear explosion there . The explosive force measured on site had been kept secret by the developers in Los Alamos from the British outside.

Trinity Explosion in New Mexico

By previous thinking on this topic Taylor was clear that the radius of the initially approximately hemispherical explosion largely on the time since the firing of the bomb, the density of the surrounding the explosion of air and of course released from the energy depends on the bomb. Other sizes are negligible. ${\displaystyle R}$ ${\displaystyle t}$ ${\displaystyle \rho }$ ${\displaystyle E}$

The following applies: ${\displaystyle R=f(t,\rho ,E)}$

and:

${\displaystyle A={\begin{pmatrix}&\mathbf {M} &\mathbf {L} &\mathbf {T} \\t&0&0&1\\\rho &1&-3&0\\E&1&2&-2\\\end{pmatrix}}\,{\text{bzw.}}\,A={\begin{pmatrix}0&0&1\\1&-3&0\\1&2&-2\\\end{pmatrix}}}$

The rank of is 3 and . The functional relationship is determined up to one constant , because it can only apply: ${\displaystyle A}$ ${\displaystyle p=n-r=3-3=0}$ ${\displaystyle c}$

${\displaystyle {\frac {R^{5}\cdot \rho }{E\cdot t^{2}}}=c^{5}\to R(t)=c\cdot {\sqrt[{5}]{\frac {E\cdot t^{2}}{\rho }}}\to E(R,t)={\frac {R^{5}\cdot \rho }{c^{5}\cdot t^{2}}}}$

With an estimated temperature at the time of explosion at about 6 am in New Mexico of ° is obtained for the air density : . ${\displaystyle T=20}$ ${\displaystyle \rho =1{,}204\,\mathrm {kg/m} ^{3}}$

The radius is about at the time in the above picture . ${\displaystyle R}$ ${\displaystyle t=0{,}025\,\mathrm {s} }$ ${\displaystyle R=130\,\mathrm {m} }$

The proportionality factor could be determined from a comparison explosion with conventional explosives (several kg of TNT ). Taylor had enough background to be able to accept. So is: ${\displaystyle c}$ ${\displaystyle c\approx 1{,}0}$

${\displaystyle E={\frac {130^{5}\cdot 1{,}204}{1{,}0^{5}\cdot 0{,}025^{2}}}=7{,}15\cdot 10^{13}\,\mathrm {J} }$

1 tonne of TNT has an energy of 4.18 billion joules . This leads to the estimation:

${\displaystyle E={\frac {7{,}15\cdot 10^{13}}{4{,}18\cdot 10^{9}}}=17.095\,{\text{Tonnen TNT}}}$

Trinity had an energy of approximately 19,000-21,000 tons of TNT, according to official information. The deviation from the above is explained by the fact that the radius is in the 5th power. The result is remarkably accurate. Taylor himself calculated about 19,000 tons of TNT. ${\displaystyle R}$

literature

• HL Langhaar: Dimensional Analysis and Theory of Models. , 166 p., John Wiley & Sons, New York London 1951, ISBN 0-88275-682-6 .
• Henry Görtler: Dimension analysis, theory of physical dimensions with applications. Springer-Verlag, Heidelberg 1975, ISBN 3-540-06937-2 .
• WJ Duncan: Physical Similarity and Dimensional Analysis. Edward Arnold & Co., London 1951, ISBN 0-7131-3042-3 .
• Wilfred E. Baker, Peter S. Westine, Franklin T. Dodge: Similarity Methods in Engineering Dynamics, Theory and Practice of Scale Modeling. Second Edition, Elsevier Science Publishers, Amsterdam 1991 (new edition), ISBN 0-444-88156-5 .
• Joseph H. Spurk: Dimensional Analysis in Fluid Mechanics. Springer, Berlin 1999, ISBN 3-540-54959-5 .
• Edgar Buckingham: On Physically Similar Systems . Illustrations of the Use of Dimensional Equations. In: Physical Review . Series II. Volume 4 , no. 4 . American Physical Society, October 1914, pp. 345-376 , doi : 10.1103 / PhysRev.4.345 .
• Edgar Buckingham: The Principle of Similitude . In: Nature . tape 96 , no. 2406 , December 9, 1915, p. 396–397 , doi : 10.1038 / 096396d0 ( nature.com [PDF; accessed June 1, 2012]).
• Helmut Kobus: Application of dimensional analysis in experimental research in civil engineering. In: The construction technology. Issue 3, Ernst & Sohn, Berlin 1974.

Web links

• Article on the work of Geoffrey Ingram Taylor In: Physics Today. (English)
• Aerospaceweb, with representations of flow resistances using similarity indicators. (English)
• Dimensional analytical methods for optimizing atomization processes in process engineering (PDF; 246 kB)
• An exploration of physics by dimensional analysis. (English)

Individual evidence

1. ↑ Taylor, The formation of a blast wave by a very intense explosion, Proc. Roy. Soc. A, Volume 101, 1950, p. 159, or Taylor, Scientific Papers, Volume 3, Cambridge UP, 1963, p. 493

This version was added to the list of articles worth reading on February 25, 2006 .