Hydrostatic

The hydrostatic is the study of still or flow-free liquids . It is a branch of fluid statics .

Hydrostatic pressure

The pressure in an ideal liquid at one point is the same in all directions. If only the force of gravity acts, the pressure of gravity (also hydrostatic pressure) corresponds to the sum of the (atmospheric) pressure on the surface and the pressure resulting from the weight of the liquid column above the point under consideration. The gravity pressure is only dependent on the depth, but not on the shape of the vessel. This is known as the hydrostatic paradox .

Basic hydrostatic equation

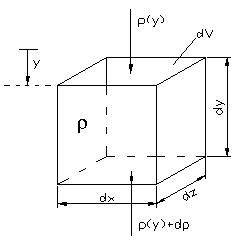
To derive the hydrostatic basic equation, the following consideration is made: In the gravitational field with the gravitational acceleration , the pressure-loaded cuboid volume element of density acts on the pressure from above . A counter pressure acts from below (from pos. To neg. Direction) . ${\ displaystyle g}$ ${\ displaystyle dV = dx \ cdot dy \ cdot dz}$ ${\ displaystyle \ rho}$ ${\ displaystyle p (y)}$ ${\ displaystyle y}$ ${\ displaystyle p (y) + dp}$

There is therefore an increase in pressure between the top and bottom of the volume element , which must be determined. For this purpose the equilibrium of forces is established in the direction : ${\ displaystyle dp}$ ${\ displaystyle y}$ ${\ displaystyle \ sum F_ {y} = 0}$

{\ displaystyle \ sum F_ {y} = p (y) \ cdot (dx \ cdot dz) + \ rho \ cdot g \ cdot (dx \ cdot dy \ cdot dz) - (p (y) + dp) \ cdot (dx \ cdot dz) = 0}

This expression can be shortened to

{\ displaystyle \ rho \ cdot g \ cdot dy-dp = 0}

In other words, the form known as the hydrostatic basic equation results :

{\ displaystyle {\ frac {dp} {dy}} = \ rho \ cdot g}

For the sake of completeness, it should be mentioned that this relationship also results as a special case of the Navier-Stokes equations from fluid mechanics. These are derived using the law of momentum for a fluid element.

The basic hydrostatic equation, assuming the incompressibility of liquids ( ), gives the pressure dependent on : ${\ displaystyle \ rho = {\ rm {const.}}}$ ${\ displaystyle y}$ ${\ displaystyle p (y)}$

{\ displaystyle \ int _ {p (0)} ^ {p (h)} dp = \ int _ {0} ^ {h} (\ rho g) dy}

{\ displaystyle \ Rightarrow p (h) = \ rho \ cdot g \ cdot h + p (0)}

With

${\ displaystyle \ rho}$ : Density of the liquid

${\ displaystyle g}$ : Gravity acceleration

${\ displaystyle h}$ : Expansion of the liquid column in the direction ${\ displaystyle y}$

${\ displaystyle p (y = 0)}$ : Pressure on the surface of the liquid column.

If the compressibility of the fluid is included in the calculation of the pressure, the following diagram results with the compressibility : ${\ displaystyle \ kappa = - {\ frac {dV} {V \ cdot dp}} = 0 {,} 5 {\ frac {1} {\ rm {GPa}}}}$

At a depth of 12,000 m , based on a density of 1000 kg / m³ at a depth of 0 m, this would result in a deviation of the calculated real pressure from the ideal of approx. 3.5%. However, temperature effects and other influences are still not taken into account.

Using a corresponding expression for , the barometric altitude formula can be developed in a similar way from the basic hydrostatic equation. ${\ displaystyle \ rho}$

Static buoyancy

If a body is placed in a liquid, the pressure on the bottom is higher than on the top. The resulting force points upwards and is called lift. The buoyancy corresponds to the weight of the displaced liquid ( Archimedes' principle ). If the average density of a body is smaller than that of the liquid, the buoyancy force outweighs the weight force. If there are no other forces acting on it, the body rises and swims. If, on the other hand, its density is greater than the liquid, the body sinks downwards; if the density is the same, it floats.

Hydraulics

Hydraulic systems use the independence of the pressure from the vessel shape. For example, if water is pressed through a pipe with a relatively small cross-section into a vessel with a large cross-section , the pressure in the pipe is equal to the pressure in the vessel. The force to be used in the pipe is . However, the force in the vessel acts on the entire cross-sectional area. It is and therefore many times larger. The hydraulic system acts here as a force amplifier. This principle is used z. B. in the hydraulic press . ${\ displaystyle A_ {1}}$ ${\ displaystyle A_ {2}}$ ${\ displaystyle p}$ ${\ displaystyle F_ {1} = p \ cdot A_ {1}}$ ${\ displaystyle F_ {2} = p \ cdot A_ {2}}$

literature

Dionysius Lardner : Handbook of Hydrostatics and Pneumatics. Printed and published by Gottfried Basse, Quedlinburg and Leipzig 1836.
Abel Bürja: Basic principles of hydrostatics. At Lagarde and Friedrich, Berlin 1790.
Bruno Eck: Technical Fluid Mechanics. Springer Verlag Berlin Heidelberg GmbH, Berlin Heidelberg 1949.

Web links

Wikibooks: Hydrostatics formula collection - learning and teaching materials

Hydrostatics lecture notes (accessed on January 4, 2015)
Hydrostatics (accessed January 4, 2015)
Fluid Mechanics (accessed January 4, 2015)
www.spektrum.de: Basic hydrostatic equation