Barometric altitude formula

Average pressure and density depending on the altitude. Logarithmic representation for great heights

Linear representation for low heights

The barometric altitude formula describes the vertical distribution of ( gas ) particles in the earth's atmosphere , i.e. the dependence of the air pressure on the altitude . Therefore we also speak of a vertical pressure - gradient , which, however, due to the high weather dynamics can be described within the lower atmosphere only approximations mathematically.

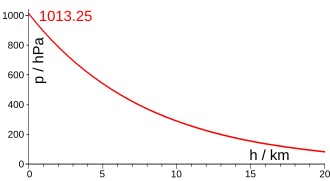
In its simplest form, it can be roughly assumed that the air pressure near sea level decreases by one hectopascal (corresponding to 1 ‰ of the mean air pressure) for every eight meters of altitude increase.

The approximation that the pressure decreases exponentially with increasing altitude is somewhat better . This connection was first recognized by Edmond Halley in 1686 .

Basic hydrostatic equation

Volume element with the decisive influences

The change in pressure and density of the atmosphere with altitude is described by the basic hydrostatic equation . To derive this, consider a cuboid volume element with the base and the infinitesimally small height , which contains air of density . From below, only the force exerted by atmospheric pressure acts on the base . The force acting on the base from above is made up of the weight of the air mass contained in the volume and the force exerted by the atmospheric pressure on the top. The atmospheric pressure at this level differs by the amount from the pressure acting on the underside; the power exercised by him is therefore . ${\displaystyle A\,}$ ${\displaystyle \mathrm {d} h\,}$ ${\displaystyle \rho \,}$ ${\displaystyle p\,}$ ${\displaystyle p\cdot A}$ ${\displaystyle \mathrm {d} m\cdot g=\rho \,\mathrm {d} V\cdot g=\rho g\,\mathrm {d} h\cdot A}$ ${\displaystyle \mathrm {d} V=A\cdot \mathrm {d} h}$ ${\displaystyle \mathrm {d} m\,}$ ${\displaystyle \mathrm {d} p\,}$ ${\displaystyle (p+\mathrm {d} p)\cdot A}$

In hydrostatic equilibrium, all air currents have come to rest. So that the equilibrium is maintained and the volume element under consideration remains at rest, the sum of all forces acting on it must be zero:

${\displaystyle p\cdot A-\rho g\,\mathrm {d} h\cdot A-(p+\mathrm {d} p)\cdot A=0}$

Shorten and rearrange supplies

${\displaystyle {\frac {\mathrm {d} p}{\mathrm {d} h}}=-\rho g}$

After the ideal gas law , the density can be expressed as , ${\displaystyle \rho \,}$ ${\displaystyle \rho ={\tfrac {pM}{RT}}}$

so that it finally results:

${\displaystyle {\frac {\mathrm {d} p}{\mathrm {d} h}}=-{\frac {pMg}{RT}}}$

It is

• ${\displaystyle M}$the mean molar mass of the atmospheric gases (0.02896 kg mol ⁻¹ ),
• ${\displaystyle g}$the acceleration due to gravity (9.807 m s ⁻² ),
• ${\displaystyle R}$the universal gas constant (8.314 J K ⁻¹  mol ⁻¹ ) and
• ${\displaystyle T}$the absolute temperature .

The basic hydrostatic equation indicates the amount by which the atmospheric pressure changes when the altitude changes by a small amount . As the negative sign shows, is negative when is positive; the pressure decreases with increasing altitude. For example, with mean air pressure at sea level (  = 1013 hPa) at a temperature of 288 K (= 15 ° C), the pressure decreases by 0.12 hPa over a one meter difference in altitude or by 1 hPa over an altitude difference of 8.3 meters. The altitude difference, which corresponds to a pressure difference of 1 hPa, is the barometric altitude level . At higher (lower ) altitudes and at higher temperatures , the air pressure changes more slowly and the barometric altitude level increases. ${\displaystyle \mathrm {d} p}$ ${\displaystyle \mathrm {d} h}$ ${\displaystyle \mathrm {d} p}$ ${\displaystyle \mathrm {d} h}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle T}$

As a rule, explicit values ​​for pressure and density are required at given heights. If necessary, the pressure differences for larger height differences can also be read from this. The desired solution of the basic equation is obtained by separating the variables

${\displaystyle {\frac {\mathrm {d} p}{p}}=-{\frac {Mg}{RT}}\,\mathrm {d} h}$

and subsequent integration between the sought heights or the associated pressures:

${\displaystyle \int _{p(h_{0})}^{p(h_{1})}{\frac {\mathrm {d} p}{p}}=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h}$.

Integration of the left results . To integrate the right side, the height dependency of and must be known. The acceleration due to gravity can be regarded as constant for not too great altitudes. The temperature varies in a complicated and unpredictable way with altitude. Simplifying assumptions about the temperature profile must therefore be made. ${\displaystyle \ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)}$ ${\displaystyle g}$ ${\displaystyle T}$ ${\displaystyle g}$ ${\displaystyle T}$ ${\displaystyle T(h)}$

Isothermal atmosphere

The classic barometric altitude formula, which is mostly cited in introductory literature and in school lessons, applies to the special case that the temperature is the same at any altitude, i.e. the atmosphere is isothermal . ${\displaystyle T}$

Derivation from the basic hydrostatic equation

The integration of the hydrostatic basic equation yields at constant : ${\displaystyle T}$

${\displaystyle {\begin{aligned}&&\int _{p(h_{0})}^{p(h_{1})}{\frac {\mathrm {d} p}{p}}&=-{\frac {Mg}{RT}}\,\int _{h_{0}}^{h_{1}}\mathrm {d} h\\\iff &&\ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)&=-{\frac {Mg}{RT}}(h_{1}-h_{0})=-{\frac {Mg}{RT}}\Delta h\\\iff &&{\frac {p(h_{1})}{p(h_{0})}}&=\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}\\\iff &&p(h_{1})&=p(h_{0})\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}\end{aligned}}}$

By introducing the scale height , the height formula is simplified to ${\displaystyle h_{s}={\tfrac {RT}{Mg}}}$

${\displaystyle p(h_{1})=p(h_{0})\mathrm {e} ^{-{\frac {\Delta h}{h_{s}}}}}$

With every increase in altitude by the air pressure decreases by the factor . The scale height is therefore a natural measure of the height of the atmosphere and the pressure profile in it. In the model atmosphere assumed here, it is around 8.4 km at a temperature of 15 ° C. ${\displaystyle h_{s}}$ ${\displaystyle \mathrm {e} \approx 2{,}7}$

The following applies to the density:

${\displaystyle \rho (h_{1})=\rho (h_{0})\mathrm {e} ^{-{\frac {\Delta h}{h_{s}}}}}$

For an observer wandering downhill, the air pressure increases steadily as an ever heavier column of air weighs down on him. The increase is exponential, because the air is compressible : for every meter of difference in height, the weight of the air column that weighs on a measuring surface increases by the weight of the column volume that is added on this distance. This weight depends on the density of the air, which in turn depends on the air pressure. The higher the air pressure is, the faster the air pressure increases (the further the observer has descended). If a variable always changes by an amount that is proportional to the variable itself, the change occurs exponentially.

Although the pressure is not constant, the air column is in mechanical equilibrium : the negative pressure gradient is equal to the force of gravity per volume element ${\displaystyle -\partial _{z}p(z)=g\rho (z)}$

Derivation from statistical mechanics

In a particle system which is in thermal equilibrium at the temperature (which therefore has the same temperature everywhere) and whose particles can occupy the continuously or discretely distributed energy levels , the probability that a particle is currently at the energy level is given by the Boltzmann distribution ${\displaystyle T}$ ${\displaystyle E_{j}}$ ${\displaystyle E_{j}}$

${\displaystyle P_{j}={\frac {\mathrm {e} ^{-{\frac {E_{j}}{k_{\mathrm {B} }T}}}}{Z}}}$.

It is the Boltzmann constant , and a normalization factor (the so-called partition ), which ensures that the sum of all probabilities equal to 1. If the system consists of particles, the number of particles at the energy level is average . ${\displaystyle k_{\mathrm {B} }}$ ${\displaystyle Z}$ ${\displaystyle N}$ ${\displaystyle E_{j}}$ ${\displaystyle n_{j}=NP_{j}}$

A gas particle of mass has the potential energy in the earth's gravitational field and, because of its temperature, has the thermal energy on average, i.e. the total energy . If one looks at two volume elements of the same size on the heights or , the particles on the heights have a higher energy by the amount . The probability of encountering a particle in the higher volume element is related to the probability of encountering it in the lower volume element as ${\displaystyle m}$ ${\displaystyle E_{\mathrm {pot} }=mgh}$ ${\displaystyle E_{\mathrm {th} }}$ ${\displaystyle E(h)=mgh+E_{\mathrm {th} }}$ ${\displaystyle h_{0}}$ ${\displaystyle h_{1}}$ ${\displaystyle h_{1}}$ ${\displaystyle mg\Delta h}$

${\displaystyle {\frac {P(h_{1})}{P(h_{0})}}={\frac {\mathrm {e} ^{-{\frac {E(h_{1})}{k_{\mathrm {B} }T}}}}{\mathrm {e} ^{-{\frac {E(h_{0})}{k_{\mathrm {B} }T}}}}}=\mathrm {e} ^{-{\frac {\Delta E}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}}$.

For a sufficiently large number of particles, the particle densities behave like the location probabilities ${\displaystyle N}$ ${\displaystyle n(h)}$

${\displaystyle {\frac {n(h_{1})}{n(h_{0})}}={\frac {NP(h_{1})}{NP(h_{0})}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}}$,

and because of the ideal gas law, the same relationship follows for the pressure ${\displaystyle p(h)=n(h)\,k_{\mathrm {B} }T}$

${\displaystyle {\frac {p(h_{1})}{p(h_{0})}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {mg\Delta h}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}}$,

where the molar mass and the gas constant are obtained by multiplying the particle mass or the Boltzmann constant by the Avogadro constant . ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle m}$ ${\displaystyle k_{\mathrm {B} }}$

However, the principle of uniform distribution is assumed here when considering energy . This requirement is generally only fulfilled in a dense atmosphere, because only there the energies between the different degrees of freedom are exchanged through collisions between the gas molecules. The reason why the uniform distribution theorem does not generally apply to the energy at altitude is that the uniform distribution theorem can only be applied directly to potentials that are included in the Hamilton function as a square. Because the altitude energy is only included in the Hamilton function linearly, one cannot simply assume the uniformity theorem in very thin gases.

Atmosphere with a linear temperature profile

The strictly linear temperature curve consists only in the idealized idea of ​​a calm atmosphere without convection without equalizing the temperature gradient through heat conduction. To make this more usable, the potential temperature was introduced. Although the adiabatic gradient is a temperature gradient, the potential temperature is constant; H. a balance. This has nothing to do with the potential energy of a particle in the gravitational field ( ). This becomes particularly clear with the number of degrees of freedom . Particles of the same mass but different numbers of degrees of freedom have different temperature gradients. ${\displaystyle E=mgh}$

Since heat conduction must not play a role in maintaining the linear temperature profile, in reality the permanent "heat transport" (heat conduction) through rapid circulation may only have a minor influence. Because the absence of convection and circulation cannot occur at the same time, the linear course is always slightly modified by heat transport of all kinds, the best known being the condensation of water vapor, which leads to a lower temperature drop ("humid-adiabatic", a somewhat misleading term).

Temperature distribution (adiabatic atmosphere)

From the equation for the change in pressure

${\displaystyle {\frac {\mathrm {d} p}{p}}=-{\frac {Mg}{RT}}\,\mathrm {d} h}$

and the equation for the adiabatic change of state, written using logarithmic derivatives

${\displaystyle {\frac {\mathrm {d} p}{p}}={\frac {\kappa }{\kappa -1}}\ {\frac {\mathrm {d} T}{T}}}$

immediately follows the linear temperature decrease according to

${\displaystyle \mathrm {d} T=-{\frac {Mg}{R\ \kappa /(\kappa -1)}}\ \mathrm {d} h}$

With the mean molar mass of the atmospheric gas M  = 0.02896 kg mol ⁻¹ , the gravitational acceleration g  = 9.807 m s ⁻² , the universal gas constant R  = 8.314 J K ⁻¹  mol ⁻¹ and the adiabatic exponent of (dry) air  = 1.402 one gets the temperature gradient ${\displaystyle \kappa }$

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} h}}=-\,{\frac {0{,}979\,\mathrm {K} }{100\,\mathrm {m} }}}$

This is approximately the temperature gradient given below. However, this is essentially determined by the wet adiabatic expansion: the wet adiabatic adiabatic exponent is smaller than the dry adiabatic adiabatic exponent. In the case of a pure water vapor atmosphere, the temperature gradient would be

${\displaystyle \left.{\frac {\mathrm {d} T}{\mathrm {d} h}}\right|_{\mathrm {H_{2}O} }=-{\frac {0{,}562\,\mathrm {K} }{100\,\mathrm {m} }}}$

Further limits of the adiabatic approach: If the air becomes very cold, the adiabatic exponent changes even if the air is dry. At very high altitudes (low density) the mean free path is also very large, so that the gas equations hardly apply. In addition, the greenhouse effect also violates the adiabatic approach (no energy exchange with the environment).

Density and pressure distribution

In general, the temperature is not constant but varies with altitude. The simplest approach to taking such variability into account is based on a linear decrease with height. A constant temperature gradient follows from the adiabatic relationship as described above

${\displaystyle a=-{\frac {\mathrm {d} T}{\mathrm {d} h}}={\frac {\kappa -1}{\kappa }}{\frac {Mg}{R}}}$

so that the following applies to the temperature : ${\displaystyle T(h)}$

${\displaystyle T(h)=T(h_{0})-a\cdot (h-h_{0})\qquad \Rightarrow \qquad T(h)=T(h_{0})\cdot \left(1-{\frac {a(h-h_{0})}{T(h_{0})}}\right)=T(h_{0})\cdot \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)}$,

where is the (positive) amount of the vertical atmospheric temperature gradient , which indicates by how many Kelvin the air temperature decreases per meter of height difference. The integral over the right-hand side of the basic equation is thus ${\displaystyle a}$

${\displaystyle -\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{R\,(T(h_{0})-a\cdot (h-h_{0}))}}\,\mathrm {d} h=-{\frac {Mg}{R}}\int _{h_{0}}^{h_{1}}{\frac {1}{(T(h_{0})+ah_{0})-ah}}\,\mathrm {d} h}$.

Because of

${\displaystyle \int {\frac {1}{b-ax}}\,\mathrm {d} x=-{\frac {1}{a}}\,\ln(b-ax)}$

is the solution of the integral

${\displaystyle -{\frac {1}{a}}\ln(\,(T(h_{0})+ah_{0})-ah)\vert _{h_{0}}^{h_{1}}=-{\frac {1}{a}}\ln \left({\frac {T(h_{0})-a(h_{1}-h_{0})}{T(h_{0})}}\right)}$,

so that overall from the integral over the basic equation

${\displaystyle \ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)=+{\frac {Mg}{R}}\,{\frac {1}{a}}\ln \left({\frac {T(h_{0})-a(h_{1}-h_{0})}{T(h_{0})}}\right)=+{\frac {Mg}{R}}\,{\frac {1}{a}}\ln \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)}$

the barometric formula for the linear temperature curve follows:

${\displaystyle p(h_{1})=p(h_{0})\mathrm {e} ^{+{\frac {Mg}{R}}{\frac {1}{a}}\ln \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)}}$,

or because of ${\displaystyle \mathrm {e} ^{y\cdot \ln(x)}=x^{y}}$

${\displaystyle p(h_{1})=p(h_{0})\left(1-{\frac {a\Delta h}{T(h_{0})}}\right)^{\frac {Mg}{Ra}}=p(h_{0})\left(1-{\frac {\kappa -1}{\kappa }}{\frac {Mg\Delta h}{RT(h_{0})}}\right)^{\frac {\kappa }{\kappa -1}}}$

The same applies to the density

${\displaystyle \rho (h_{1})=\rho (h_{0})\left(1-{\frac {a\Delta h}{T(h_{0})}}\right)^{\frac {Mg}{Ra\kappa }}=\rho (h_{0})\left(1-{\frac {\kappa -1}{\kappa }}{\frac {Mg\Delta h}{RT(h_{0})}}\right)^{\frac {1}{\kappa -1}}}$

The exponent is divided by here , since the density / pressure relationship results from the adiabatic relationship between the two quantities. ${\displaystyle \kappa }$

This extended barometric altitude formula forms the basis for the barometric altitude function of the standard atmosphere in aviation . First, the atmosphere is divided into sub-layers, each with a linear interpolated temperature profile. Then, starting with the lowest layer, the temperature and pressure at the upper limit of the respective sub-layer are calculated and used for the lower limit of the layer above. In this way, the model for the entire atmosphere is created inductively.

Typical temperature gradients

As measurements of the temperature profiles in the atmosphere show, the assumption of a linear temperature decrease on average is a good approximation, even if significant deviations can occur in individual cases, for example in inversion weather conditions . The main cause of the decrease in temperature with altitude is the warming of the lower air layers by the surface of the earth heated by the sun, while the upper air layers radiate heat into space. In addition, there are dry adiabatic or wet adiabatic temperature changes of individual ascending or descending air parcels and additional modifications due to mixing processes between air masses of different origins.

In hot air masses and during gliding processes, the temperature gradient takes on values ​​around 0.3 to 0.5 K per 100 m, in cold air usually around 0.6 to 0.8 K per 100 m, on average over all weather conditions 0.65 K per 100 m. In valleys, frequent soil inversions can lower the mean temperature gradient to 0.5 K per 100 m, in the winter months even to 0.4 K per 100 m.

The conditions described are limited to the troposphere . In the stratosphere , the temperature decreases much more slowly, in most cases it even increases again, mainly because of the absorption of UV radiation in the ozone layer .

For a temperature gradient of 0.65 K per 100 m, the exponent takes the value 5.255: ${\displaystyle \mathrm {\tfrac {Mg}{Ra}} }$

${\displaystyle p(h_{1})=p(h_{0})\left(1-{\frac {0{,}0065\cdot \Delta h}{T(h_{0})}}\right)^{5{,}255}}$

If the exponent is expressed by the isentropic coefficient, then: ${\displaystyle \kappa }$

${\displaystyle 5{,}255={\frac {\kappa }{\kappa -1}}\quad \Rightarrow \quad \kappa =1{,}235}$

That means 8.5 degrees of freedom .

The mean heat capacity of the air over all weather conditions results from the temperature gradient:

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} h}}={\frac {0{,}65\,\mathrm {K} }{100\,\mathrm {m} }}={\frac {g}{c_{p}}}={\frac {9{,}81\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}}{c_{p}}}\quad \Rightarrow \quad c_{p}=1509\,{\frac {\mathrm {m} ^{2}}{\mathrm {K} ~\mathrm {s} ^{2}}}=1509\,{\frac {\mathrm {Ws} }{\mathrm {kg~K} }}}$

This value lies between the value of dry air (1005 Ws / (kg K)) and water vapor (2034 Ws / (kg K)).

The following table shows the relationship between height and pressure (on average):

The temperature profile of the atmosphere as a function of the pressure altitude (earth's surface = 1.013 bar) - the tropopause is best approximated with an isentropic exponent of 0.19.

Height in m	Pressure in hPa
0	1013.25
500	954.61
1000	898.76
1500	845.58
2000	794.98
2500	746.86
3000	701.12
3500	657.68
4000	616.45
4500	577.33
5000	540.25
6000	471.87
7000	410.66
8000	356.06
9000	307.48
10,000	264.42
11000	226.37

In this form, the altitude formula is suitable for the frequent case that temperature and air pressure are known at one of the two altitudes, but not the currently existing temperature gradient.

The altitude levels

The barometric altitude level is the vertical distance that must be covered in order to achieve a 1 hPa air pressure change. Near the ground, the barometric altitude is around 8 meters, at 5.5 kilometers at 16 meters and at 11 kilometers at 32 meters.

With the altitude formula, the following table results for the altitude and temperature dependence of the barometric altitude level:

	Barometric altitude level in m / hPa
H	−15 ° C	0 ° C	15 ° C	30 ° C
0 m	7.5	7.9	8.3	8.8
500 m	7.9	8.3	8.7	9.2
1000 m	8.3	8.7	9.2	9.6
2000 m	9.3	9.7	10.1	10.6
3000 m	10.4	10.8	11.2	11.6

The rule of thumb for medium altitudes and temperatures is “1 hPa / 30 ft”. Aviators often use this rounding value for rough calculations.

International height formula

If one sets the reference altitude at sea level and assumes an average state for the atmosphere there, as described by the International Standard Atmosphere (temperature 15 ° C = 288.15 K, air pressure 1013.25 hPa, temperature gradient 0.65 K per 100 m ), one obtains the international altitude formula for the troposphere (valid up to 11 km altitude): ${\displaystyle h_{0}}$

${\displaystyle p(h)=1013{,}25\cdot \left(1-{\frac {0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}\cdot h}{288{,}15\ \mathrm {K} }}\right)^{5{,}255}\mathrm {hPa} }$

${\displaystyle {\color {White}p(h)}=p_{0}\cdot \left(1-{\frac {0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}\cdot h}{T_{0}\ }}\right)^{5{,}255}}$

This formula allows the calculation of the air pressure (in the form of the so-called normal pressure ) at a given altitude without the temperature and temperature gradient being known. The accuracy in the specific application is limited, however, since the calculation is based on a mean atmosphere instead of the current atmospheric state .

International altitude formula resolved according to altitude within the framework of the International Standard Atmosphere, to convert the air pressure p (h) (normal pressure) into the corresponding altitude in meters (m):

${\displaystyle h={\frac {288{,}15\ \mathrm {K} }{0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}}}\cdot \left(1-\left({\frac {p(h)}{1013{,}25\,\mathrm {hPa} }}\right)^{\frac {1}{5{,}255}}\right)}$

General case

The solution to the basic hydrostatic equation is general

${\displaystyle \ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h}$,

respectively

${\displaystyle p(h_{1})=p(h_{0})\,\mathrm {e} ^{-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h}}$

with an integral to be solved.

Virtual temperature

The gas constant is a natural constant and can be drawn in front of the integral. The mean molar mass of the atmospheric gases is also practically constant within the troposphere, provided that the highly variable water vapor content is disregarded and can also be drawn in front of the integral. The different scale heights of the atmospheric gases with different weights would lead to partial segregation in a still atmosphere, so that heavier components would accumulate in the lower layers and lighter components in the higher layers; However, the intensive mixing of the troposphere caused by the weather prevents this. The changing water vapor content and, in general, other minor changes in M (especially in the higher atmospheric layers) can be taken into account by using the corresponding virtual temperature instead of the actual temperature . The value for dry air at sea level can therefore be used for M. ${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle T_{v}}$ ${\displaystyle T}$

Geopotential heights

The acceleration due to gravity decreases with altitude, which must be taken into account in the case of large altitude differences or high accuracy requirements. A variable acceleration of gravity in the integrand would make the integration considerably more difficult. This can be avoided by using geopotential instead of geometric heights. Just imagine a test mass with a variable from sea level raised to the height . Because it decreases with altitude, the potential energy gained is smaller than if it always had the sea level value. The geopotential height is the height, measured in geopotential meters, which has to be overcome mathematically in order to add the same potential energy to the mass with constant gravitational acceleration (in other words: it is divided by the gravitational potential. Areas of the same geopotential height are equipotential surfaces in the gravitational field). ${\displaystyle g}$ ${\displaystyle m}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle g}$ ${\displaystyle \Delta E_{\mathrm {pot} }}$ ${\displaystyle g}$ ${\displaystyle g_{0}}$ ${\displaystyle h_{p}}$ ${\displaystyle g_{0}}$ ${\displaystyle \Delta E_{\mathrm {pot} }}$ ${\displaystyle h_{p}}$ ${\displaystyle g_{0}}$

For the geopotential height belonging to a geometric height , the following should apply: ${\displaystyle h}$ ${\displaystyle h_{p}}$

${\displaystyle \Delta E_{\mathrm {pot} }=\int _{0}^{h}mg(h)\,\mathrm {d} h=mg_{0}\cdot h_{p}}$,

From which follows:

${\displaystyle g(h)\,\mathrm {d} h=g_{0}\,\mathrm {d} h_{p}}$.

For the ratio of the acceleration due to gravity at altitude to the acceleration due to gravity at sea level, the following applies, since the gravitational field decreases quadratically with the distance from the center of the earth: ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle g_{0}}$

${\displaystyle {\frac {g(h)}{g_{0}}}=\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}}$,

with the radius of the earth . Integration of ${\displaystyle R_{\mathrm {E} }}$

${\displaystyle \mathrm {d} h_{p}={\frac {g(h)}{g_{0}}}\,\mathrm {d} h=\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}\mathrm {d} h}$

supplies

${\displaystyle \int _{0}^{h_{p}}\mathrm {d} h_{p}=\int _{0}^{h}\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}\mathrm {d} h}$

${\displaystyle \iff \ h_{p}={\frac {R_{\mathrm {E} }\cdot h}{R_{\mathrm {E} }+h}}}$.

${\displaystyle R_{\mathrm {E} }}$should be set to the value 6356 km. If necessary, it must also be taken into account that the acceleration due to gravity at sea level depends on the geographical latitude. ${\displaystyle g_{0}}$

In this way, the desired geometric heights have to be converted into geopotential heights only once before the calculation; Instead of the variable acceleration due to gravity, the constant sea level value can simply be used in the altitude formula. For heights that are not too great, the difference between geometric and geopotential heights is small and often negligible:

geometric	geopotential
0 m	0.0 m
500 m	500.0 m
1000 m	999.8 m
5000 m	4996.1 m
10,000 m	9984.3 m

With the acceleration of gravity at sea level , the geopotential heights and and the virtual temperature , the general height of the formula simplifies to ${\displaystyle g_{0}}$ ${\displaystyle h_{p0}}$ ${\displaystyle h_{p1}}$ ${\displaystyle T_{v}}$

${\displaystyle p(h_{1})=p(h_{0})\cdot \exp \left(-{\frac {Mg_{0}}{R}}\int _{h_{p0}}^{h_{p1}}{\frac {1}{T_{v}(h_{p})}}\,\mathrm {d} h_{p}\right)}$.

It remains to solve the integral , for which only the temperature profile has to be known. It can be determined in the real atmosphere, for example, by radiosonde ascents . For simplified model atmospheres with constant or linearly variable temperature, height formulas of the type discussed at the beginning are again obtained. ${\displaystyle 1/T_{v}}$ ${\displaystyle T_{v}(h_{p})}$

Applications

Reduction to sea level

theory

The air pressure (QFE) measured by a barometer depends on both the meteorological state of the atmosphere and the altitude. If the information from different barometers is to be compared with one another in a larger area for meteorological purposes (for example to determine the location of a low pressure area or a front), the influence of the elevation must be removed from the measurement data. For this purpose, the measured pressure values ​​are converted to a common reference altitude, usually sea ​​level . This conversion is done using an altitude formula. The conversion is also referred to as a reduction (even if the numerical value increases), since the measured value is freed from undesired interference effects. The result is the air pressure reduced at sea level (QNH).

A suitable height formula must be used depending on the accuracy requirements. For lower demands, for example, a fixed conversion factor can be derived from the altitude formula for constant temperature, for which a representative temperature must be selected:

${\displaystyle p_{0}=p(h)\,\mathrm {e} ^{+{\frac {Mg}{RT}}h}}$

For a site altitude of 500 m and using an annual mean temperature of 6 ° C, the result is e.g. B. a reduction factor of 1.063, by which the measured values ​​are to be multiplied.

For slightly higher demands, at least the current air temperature should be taken into account. Their influence is shown in the following example, in which an air pressure of 954.3 hPa measured at an altitude of 500 m is reduced with the altitude formula for a linear temperature profile ( a = 0.0065 K / m) assuming different station temperatures at sea level: ${\displaystyle T(h)}$

${\displaystyle p_{0}=p(h)\,\left({\frac {T(h)}{T(h)+0{,}0065\,h}}\right)^{-5{,}255}}$

t (h)	−10 ° C	0 ° C	10 ° C	20 ° C	30 ° C
p 0	1017.9	1015.5	1013.3	1011.2	1009.3

${\displaystyle T(h)=t(h)+273{,}15}$

Using an incorrect temperature can therefore lead to deviations of a few hPa. If higher accuracy is desired, current air temperatures are available and the accuracy and calibration of the barometer used justify the effort, the reduction should always be made using the current air temperature. The variant for a linear temperature curve can be used as an altitude formula. However, the variant for a constant temperature profile can just as well be used, provided that the current temperature that is halfway up the station is used:

${\displaystyle p_{0}=p(h)\,\mathrm {e} ^{+{\frac {Mg}{R\,\left(T(h)+a{\frac {h}{2}}\right)}}h}}$

This variant is theoretically a little less precise, because it ignores the variability of temperature with altitude, while the linear variant takes this into account at least to some extent. However, the differences are completely insignificant when it comes to the heights and temperatures usually occurring for weather stations.

The reduction formula recommended by the German Weather Service corresponds to the variant with a constant temperature curve. From the temperature measured at site altitude, the temperature at half site altitude is estimated with the aid of the standard temperature gradient. The air humidity is taken into account through the transition to the corresponding virtual temperature.

${\displaystyle p_{0}=p(h)\,\mathrm {e} ^{x},\quad x={\frac {g_{0}}{R^{*}\,(T(h)+C_{h}\cdot E+a{\frac {h}{2}})}}\,h}$

With

${\displaystyle p_{0}}$		Air pressure reduced to sea level
${\displaystyle p(h)}$		Air pressure at barometer height (in hPa, accurate to 0.1 hPa)
${\displaystyle g_{0}}$	= 9.80665 m / s²	Standard acceleration
${\displaystyle R^{*}}$	= 287.05 m 2 / (s²K)	Gas constant of dry air (= R / M)
${\displaystyle h}$		Barometer height (in m, to the nearest dm; up to 750 m height can be calculated with the geometric height, above that geopotential heights are to be used)
${\displaystyle T(h)}$		Cabin temperature (in K, where ) ${\displaystyle T(h)=t(h)+273{,}15\,\mathrm {K} }$
${\displaystyle t(h)}$		Cabin temperature (in ° C)
${\displaystyle a}$	= 0.0065 K / m	vertical temperature gradient
${\displaystyle E}$		Vapor pressure of the water vapor fraction (in hPa)
${\displaystyle C_{h}}$	= 0.12 K / hPa	Coefficient for taking into account the mean vapor pressure change with altitude (actually station-dependent, here as a fixed mean value) ${\displaystyle E}$

If no measured air humidity is available, the following approximation can also be used, which is based on long-term mean values ​​of temperature and humidity: ${\displaystyle E}$

${\displaystyle t(h)<9{,}1\,^{\circ }\mathrm {C} :{\tilde {E}}=5{,}6402\cdot (-0{,}0916+\mathrm {e} ^{0{,}06\cdot t(h)})}$

${\displaystyle t(h)\geq 9{,}1\,^{\circ }\mathrm {C} :{\tilde {E}}=18{,}2194\cdot (1{,}0463-\mathrm {e} ^{-0{,}0666\cdot t(h)})}$

practice

The comparison of several barometers shows the limited absolute accuracy of commercially available devices.

The accuracy requirements for measured air pressure and barometer height that are collected here will usually not be able to be met by an amateur meteorologist. With the barometers of Hobby weather stations , systematic errors of at least 1 to 2 hPa are to be expected. Such an uncertainty corresponds to an uncertainty of the site altitude of ten to twenty meters via the barometric altitude level. The ambition to determine the location height more precisely will most likely not lead to a more precise result. In this light, the necessity or superfluous consideration of the air humidity should also be considered.

If necessary, it is advisable not to use the real altitude, but a fictitious altitude that best matches the reduced air pressure with the information from a nearby reference barometer (official weather station, airport, etc.). A possible systematic error of the barometer can be largely compensated by such a calibration . For this purpose, it is advisable to first use an approximate level for the reduction and to compare your own results with the reference information over a longer period of time (especially at different temperatures). If a systematic difference is found, the height difference can be calculated using a suitable height formula, which, based on the approximate location height, shifts the reduced heights by the desired amount. The amount corrected in this way is then used for future reductions. If the temperature is not taken into account during the reduction, calibration should be based on the situation at a representative temperature.

A typical living room barometer

Simple living room barometers are usually set so that they immediately show the reduced air pressure. This is usually done using a screw on the back of the housing, which can be used to change the preload of the pressure cell spring . The calibration therefore corresponds to a shift in the display scale. Strictly speaking, this is incorrect. As the altitude formulas show, the reduction must be done by multiplying by a calibration factor and not by simply adding a constant: The reduced air pressure changes by a little more than one hPa if the air pressure at the site altitude changes by one hPa. The scale would therefore have to be stretched slightly in addition to the shift. The error caused by this, however, is smaller than the error that arises from the fact that these devices ignore the influence of temperature on the reduction. Since they have no option to enter the altitude, calibration can only be carried out by comparison with a reference barometer, which in turn reduces systematic zero point errors of the instrument at the same time. The calibration must be carried out for the location of the barometer (or a location of comparable altitude). There is no point in having the device “properly set” at the dealer if it is then hung in a completely different location. If the barometer is used from air pressure changes derive a short-term weather forecast, precise calibration is less important.

Limits

In general, when reducing air pressure measurements, it should be borne in mind that the arithmetically added air column can not actually exist for most locations and therefore there can not be a “true” value for the “sea level pressure at the location” that can be calculated precisely through sufficiently complex calculations could be approximated. The reduction formulas are partly based solely on conventions and, apart from special scientific applications, mainly serve to make the measured values ​​of the weather stations as comparable as possible. An example of the fictivity of the added air column: Over level terrain, on which cold air does not flow away, the air near the ground can cool down noticeably on clear nights due to the heat radiation of the ground ( ground inversion ). A weather station located there will register this reduced temperature and continue mathematically with the usual temperature gradient downwards. If the terrain were at sea level, however, that air would not have cooled down at all because of the lack of soil and the air column that actually exists would have a significantly higher temperature than the calculated one. The calculation has assumed too high a density of the added air column and results in a higher reduced air pressure than would exist in the same weather situation, if the entire area were at sea level.

Barometric altitude measurement

→ Main article : Barometric altitude measurement

The altitude dependency of the air pressure can also be used for altitude measurement . Barometric altitude measurements are quick and relatively easy to perform, but their accuracy is limited. A barometer designed for determining altitude is called an altimeter or altimeter . The procedure depends on the intended use and accuracy requirements. The method is used, among other things, for hiking and, with somewhat higher accuracy requirements, in land surveying.

literature

• Richard Rühlmann : The barometric height measurements and their significance for the physics of the atmosphere. Leipzig 1870, pp. 10–12, 21–24 ( digital ). (about history)

• W. Roedel: Physics of our environment: The atmosphere. 3. Edition. Springer-Verlag, Berlin / Heidelberg / New York 2000, ISBN 3-540-67180-3 .

See also

• Above sea level

Web links

Wikibooks: Hydrostatics formula collection  - learning and teaching materials

• Online calculation program for the international height formula

Individual evidence

1. ^ Edmond Halley : A discourse of the rule of the decrease of the height of the mercury in the barometer . In: Philos. Transactions , 1686 and 1687, Vol. 16, p. 104
2. ↑ K.-H. Ahlheim [ed.]: How does it work? Weather and climate. Meyers Lexikonverlag, Mannheim / Vienna / Zurich 1989, ISBN 3-411-02382-1 , p. 46
3. ↑ Observer's manual (BHB) for weather reporting points of the synoptic-climatological measurement and observation network . accessed on January 20, 2016