Equal distribution theorem
The uniform distribution theorem (also called equipartition theorem ) is a theorem from statistical physics that establishes a connection between the mean value of the energy of a system in thermal equilibrium and its temperature . Its key message is that in thermal equilibrium every degree of freedom of the system has the same mean energy, regardless of the masses and other properties of the particles and of the composition of the system.
The equal distribution of the kinetic energy is shown accordingly also z. B. in gas mixtures, with free neutrons in a moderator or in the plasma of a fusion reactor .
The uniform distribution theorem only applies to degrees of freedom that are actually excited in thermal equilibrium, that is, are not "frozen" . For example, molecular vibrations of molecules such as H 2 or O 2 are not excited at room temperature because the energy required for the transition to excited states is not achieved.
Degrees of freedom, the variables of which do not appear in the Hamilton function , also do not contribute to the energy.
The uniform distribution theorem is a strictly valid result of classical statistical mechanics and also applies to relativistic energies. However, due to the possibility of freezing the degrees of freedom within the framework of quantum statistics, it only applies at a sufficiently high temperature. This leads to the fact that the uniform distribution theorem is also invalid for some classical problems of classical physics, namely with the ultraviolet catastrophe and with deviations of the specific heat capacity of solids from the Dulong-Petit law .
history
First formulations
First considerations, which contain statements of the uniform distribution theorem, were given by the Scottish physicist John James Waterston as part of his investigation of the kinetic theory of gases. Waterston found that thermal equilibrium is reached when the vis viva , a historical name for twice the kinetic energy of each particle, is the same. Since the kinetic gas theory was not yet established at this point in time, its results were forgotten.
James Clerk Maxwell stated in 1878 that at a given temperature the total kinetic energy of a system must be the product of the degrees of freedom of a system with a universal constant. This enabled him to theoretically explain the Dulong-Petit law, which had already been known experimentally since 1819. The uniformity theorem received further confirmation from measurements of the specific heat capacity of noble and other monatomic gases such as mercury vapor.
Problems of the Equal Distribution Theorem
Despite these successes, the Dulong-Petit law failed, particularly with the specific heat capacity of diamonds . Further investigations by Heinrich Friedrich Weber on the heat capacity of carbon, boron and silicon showed that the Dulong-Petit law and thus also the uniform distribution theorem are only valid for sufficiently high temperatures. These deviations from the Dulong-Petit law could be explained for the first time by the Einstein model set up by Albert Einstein , which takes quantum mechanics into account.
In addition, Arnold Eucken found out through measurements on hydrogen gas that its heat capacity drops from about 5 cal / (mol K) at room temperature to 3.3 cal / (mol K) at 60 K, and then remains approximately constant. This is the value predicted by the uniformity theorem for monatomic gases; for diatomic ones, however, he predicts a heat capacity of 7 cal / (mol K). Eucken found that his measurements on hydrogen could not be reconciled with the predictions of the Einstein model. Only further findings from quantum mechanics could explain that some degrees of freedom in polyatomic gases are not excited at low temperatures.
The most famous erroneous prediction of the theorem of uniformity is known as the ultraviolet disaster. It follows inevitably from the assumption of the universal validity of the Rayleigh-Jeans law for the energy density of the radiation from a black body : According to the uniform distribution theorem, every oscillation mode should have the same energy; this leads to the spectral energy density becoming arbitrarily large due to the contribution of the small wavelengths. This problem can also be solved by including quantum mechanics, as Max Planck had shown in 1900 with his law of radiation .
Concluding on the relationship between quantum mechanics and the uniform distribution theorem, Einstein was able to show in 1924 when investigating Bose gases that the uniform distribution theorem is valid when the particle density is sufficiently small and the temperatures high enough, i.e. exactly when the classical Limes can be formed.
Mathematical formulation
statement
The most general statement of the equal distribution theorem is
With
- the ensemble mean
- the Hamilton function of the system
- the temperature of the system
- the Boltzmann constant
- the Kronecker Delta
- the phase space coordinates
The phase space coordinates are the impulses or the locations . Therefore, with the aid of Hamilton's equations of motion, the uniform distribution theorem can be used as an alternative for the locations and momenta
respectively
are shown, with a point above the variable denoting the total time derivative.
The uniform distribution theorem is particularly useful when the Hamilton function breaks down into individual summands that only depend on a single degree of freedom and all of these degrees of freedom occur in an identical power, that is, if
with constants is. Then:
Since all phase space variables are independent and therefore uncorrelated , therefore holds
or
- .
The condition placed on the Hamilton function applies in particular to the kinetic energy of a system made up of free particles, in which only the momentum components enter quadratically ( ), and for particles in a harmonic potential , into which the spatial components also enter quadratically.
In general, this statement also applies to more general Hamilton functions of the form
- .
Derivation from statistical mechanics
The starting point for deriving the principle of equal distribution is a closed system that is energetically coupled to a heat bath . It is therefore advisable to consider the canonical ensemble . Then with the definition of the ensemble mean:
The integration takes place over the entire accessible phase space . denotes the inverse temperature and the canonical partition function . Partial integration lists
where the boundary term falls off quickly enough due to the exponential of the Hamilton function that it vanishes. It stays:
The derivation was carried out here using the canonical ensemble, it also means microcanonical ensembles possible. The uniform distribution theorem cannot be derived in the grand canonical ensemble , but all ensembles are equivalent for large numbers of particles, so that it also applies to open systems.
Derivation for ideal gases from the kinetic gas theory
For an ideal gas whose Hamilton function only contains the kinetic component, the uniform distribution theorem can be derived using the Maxwell-Boltzmann distribution . This distribution indicates the probability density with which a particle has a certain speed and reads:
With the Hamilton function , its expected value can be calculated as the expected value of the speed square. The following applies:
Connection with the virial theorem
The virial theorem establishes a connection between the mean value of the kinetic energy over time and the potential of a system. It reads with the force on each particle
where the sum runs over all particles of a system and the overline symbolizes the time average.
For conservative forces , a statement can be derived from the uniform distribution theorem that is similar to the virial theorem, but replaces the time mean with the ensemble mean. For conservative forces, the momentum is a monomial in the Hamilton function and it holds
where is the -th momentum component of the -th particle. On the other hand is
for each . Therefore applies
and thus:
In general, the ergodic hypothesis states that time means and ensemble means coincide in ergodic systems. Conversely, it can be shown that the ergodicity of the system for a derivation of the uniform distribution theorem in the micro-canonical ensemble, if a system does not interact with its environment, cannot be dispensed with.
Applications
Heat capacity of solids, Dulong-Petit law
In the case of solids, the oscillation of the atoms around their position of rest can be approximated by the potential of a harmonic oscillator . The associated energy is through for each spatial direction
given, where is the angular frequency of the oscillator and means the deflection of the atom from its rest position in the direction . (The individual atoms can also have different frequencies.) The first term is the kinetic energy , the second the potential energy . So there are two degrees of freedom per atom and space dimension as a square, i.e. six degrees of freedom per atom in three dimensions. Hence the mean energy per atom
For atoms ( is Avogadro's constant ), degrees of freedom must be taken into account. The molar heat capacity of
This equation is known as the Dulong-Petit law . Deviations, as they have already been observed with boron, carbon and silicon at normal temperatures, can only be understood through quantum mechanics. The deviations result from the fact that not all degrees of freedom are excited if the temperature is not sufficiently high. Quantum physical models for calculating the heat capacity are the Einstein model from 1907 and the significantly improved Debye model from 1912. They contain the Dulong-Petit law as a limiting case at high temperatures.
Heat capacities of ideal gases
Monatomic ideal gas
For particles that only interact with each other through hard elastic collisions (monatomic ideal gas ), in three spatial dimensions the Hamilton function consists only of the kinetic part:
Applying the above result
delivers:
That means, per degree of translational freedom (here ) is the mean kinetic energy . Its molar heat capacity is accordingly
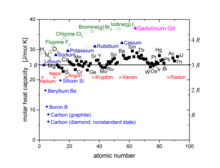
which also agrees well with the measured heat capacities for the noble gases (red in the diagram above).
Diatomic ideal gas
For a diatomic ideal gas - the individual molecules only interact with each other through hard elastic collisions and cannot rotate around the molecular axis - the Hamilton function with a constant moment of inertia (i.e. neglecting the rotation-vibration coupling) is
where is the total mass, the reduced mass and the moment of inertia of a molecule. describes the deflection from the equilibrium distance. Altogether, seven sizes go squarely into the Hamilton function: . It follows:
and
- .
In practice, for most diatomic real gases, only an approximate interaction is measured . This is due to the fact that the vibration degrees of freedom are usually not excited at room temperature. The weaker the bond between the atoms, the sooner this process takes place and degrees of freedom from vibrations lead to a contribution to the heat capacity, as can be seen in the diagram above for the halogens (in green).
Relativistic ideal gas
In the special theory of relativity the Hamilton function of the ideal gas reads
- ,
where is the speed of light . In particular, the simplified form of the uniform distribution theorem cannot be applied directly to a Hamilton function of this form in order to establish a connection between the expected value of the Hamilton function and the temperature of the gas. For the highly relativistic Limes, i.e. in the case of high particle energies , the Hamilton function can be used as
to be approached. It follows that in the relativistic Limes the uniform distribution theorem
supplies. The specific heat capacity for highly relativistic gases increases accordingly
- .
Thermal equation of state of real gases
For a real gas in a container, the Hamilton function is
- ;
is the potential between the wall and the particle, the potential between the particles. For a cube-shaped container with a side length , the wall potential is written e.g. B. as follows:
The Heaviside function was used for this. The application of the virial theorem (in the sense of quantum mechanics) yields:
The first term on the right is
- .
It was exploited that the distributive derivative of the Heaviside function is the delta distribution . is the volume . Since the pressure is defined by (see e.g. canonical ensemble ), the ensemble averaging results
- .
This gives the thermal equation of state:
This corresponds to the ideal gas equation , which is expanded by an additional term - the virial . The virial can be developed in powers of the particle density (see: Virial development ).
Counterexample: quantum mechanical harmonic oscillator
A one-dimensional quantum mechanical harmonic oscillator has the Hamilton operator
- .
With the occupation number operator and Planck's reduced quantum of action , it can be described as
rewrite. The expected energy value results from the quantum statistics (with the inverse temperature ) to
For low temperatures, therefore , is ; the classic uniform distribution theorem only applies for sufficiently high temperatures .
Individual evidence
- ^ Clifford Truesdell: Essays in the History of Mechanics . Springer, Berlin Heidelberg New York 1968, p. 292-299 .
- ↑ James Clerk Maxwell: On Boltzmann's theorem on the average distribution of energy in a system of material points . In: William Davidson Niven (Ed.): The Scientific Papers of James Clerk Maxwell . tape 2 . Dover, New York 1965, pp. 713-741 .
- ^ Heinrich Friedrich Weber: The specific warmth of the elements carbon, boron and silicon . In: Annals of Physics . tape 230 , no. 3 , 1875, p. 367-423 .
- ↑ Arnold Eucken: The molecular heat of hydrogen at low temperatures . In: Meeting reports of the German Academy of Sciences in Berlin . tape 1912 , no. 1 , 1912, p. 141-151 .
- ↑ Albert Einstein: Quantum theory of the monatomic ideal gas . In: Meeting reports of the Prussian Academy of Sciences . 1924.
literature
- Schwabl : Statistical Mechanics. Springer-Verlag, Berlin, 3rd edition 2006, ISBN 978-3-540-31095-2 .























![{\ displaystyle \ left \ langle x_ {i} {\ frac {\ partial H} {\ partial x_ {j}}} \ right \ rangle = {\ frac {1} {\ beta Z}} \ int \ mathrm { d} \ Gamma \, {\ frac {\ partial x_ {i}} {\ partial x_ {j}}} e ^ {- \ beta H} - {\ frac {1} {\ beta Z}} \ left [ x_ {i} e ^ {- \ beta H} \ right] _ {x_ {j} = - \ infty} ^ {x_ {j} = \ infty},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faf6d3067d198e19305decd0606a8e576268188b)























































![{\ displaystyle V _ {\ mathrm {Wall}} = A \ sum _ {i = 1} ^ {3N} \ left [\ Theta (q_ {i} -L) + \ Theta (-q_ {i}) \ right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68a149aa609169ad4f58ad56a7dc79836cd64f2e)

![{\ displaystyle {\ begin {aligned} \ sum _ {i = 1} ^ {3N} q_ {i} {\ frac {\ partial V _ {\ mathrm {wall}}} {\ partial q_ {i}}} & = \ sum _ {i = 1} ^ {3N} q_ {i} A \ left [\ delta (q_ {i} -L) - \ delta (q_ {i}) \ right] = \ sum _ {i = 1} ^ {3N} LA \ delta (q_ {i} -L) \\ & = - L {\ frac {\ partial V _ {\ mathrm {wall}}} {\ partial L}} = - L {\ frac {\ partial H} {\ partial L}} = - L {\ frac {\ partial V} {\ partial L}} {\ frac {\ partial H} {\ partial V}} = - 3V {\ frac {\ partial H} {\ partial V}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab2dca96e6e753b0ff6e84523a40f2a360e7640c)















