Atmospheric temperature gradient
The atmospheric temperature gradient (also called thermal altitude gradient ) is the vertical temperature gradient in the earth's atmosphere . To put it simply, it describes how much the air temperature increases or decreases with altitude.
The horizontal temperature gradient, especially between the equator and the poles , is called the meridional temperature gradient . It plays an important role as a driving factor for planetary circulation and in the energy balance of the earth . It is positive from both poles to the equator, with an average of -33 ° C ( south pole ), or -23 ° C ( north pole ) up to 26 ° C (equator).
The temperature gradient in the layers of the earth's atmosphere

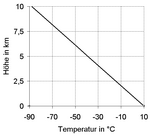
If you look at the entire earth's atmosphere in the vertical direction, the atmospheric temperature gradient (see red line in the adjacent graphic) is reversed a total of three times, as follows:
- In the troposphere (up to approx. 15 km) it is mostly negative, so the air temperature decreases with altitude (to approx. −50 ° C at the height of the tropopause ). Its regional mean is −6 ° C per km . In detail, however, the extent of this temperature drop is very different and in some areas it can also turn into a temperature rise ( inversion weather situation ). The actually measurable and thus static ambient gradient is distinguished from two dynamic gradients of moving air parcels. The two dynamic gradients, in their interaction with the static gradient of the state air, are responsible for the stratification stability of the troposphere .
- In the stratosphere (approx. 15–50 km) the atmospheric temperature gradient is initially neutral ( isothermal at approx. −50 ° C) and positive towards the top (air temperature rises to approx. 0 ° C at the level of the stratopause ).
- In the mesosphere (approx. 50–80 km) it is negative again (air temperature drops to approx. −90 ° C at the height of the mesopause ).
- In the thermosphere (approx. 80–500 km) and the exosphere (> 500 km) it is positive again (up to the temperatures in space ).
In meteorology , one restricts oneself to the temperature gradient of the troposphere and usually only considers its vertical component, i.e. the change in air temperature with increasing distance from the earth's surface. The temperature profile of the layers of the atmosphere above, however, is of little significance for the weather.
Basics
theory
Closely related to the change in temperature in the vertical are, on the one hand, the change in air pressure caused by gravity (see barometric altitude formula ) and, on the other hand, energy transport processes via sensible and latent heat , i.e. ultimately a transition from thermal to potential energy . It is a phenomenon that can only be explained on the basis of thermodynamics and kinetic gas theory . The various gas laws serve as a theoretical basis . For simple processes can be the Ideal Gas Law as a state equation use, but only as long as the air is a nearly ideal behavior shows.
The coupling between pressure and temperature depends on the change in state. A decrease in air pressure corresponds to an increase in altitude and, conversely, an increase in air pressure corresponds to a decrease in altitude.
An air parcel that moves vertically up or down in the atmosphere experiences an adiabatic change in state, so no heat is supplied or withdrawn from outside and no mixture with the ambient air occurs. The adiabatic change in temperature of such air parcels is solely due to a decrease in pressure when rising, or an increase in pressure when falling. This circulation exists because the radiation conditions in a still atmosphere result in a temperature gradient that is above the adiabatic limit value, so the air stratification becomes unstable and circulation results. The adiabatic assumption is a simplifying assumption that must be assumed for dynamic gradients and is mostly valid in a good approximation due to the poor mixability and poor heat conduction properties. However, the warming effects of the radiation can be seen near the ground, so generally no adiabatic process can be estimated here. Dynamic processes must also be taken into account, such as the sliding of warm air onto cold air, which are also not recorded by assuming an adiabatic process. There is no adiabatic gradient in the stratosphere . The reason is that pure radiation transport does not result in a temperature gradient above the adiabatic limit value. Due to the absorption of UV radiation (heating), the temperature gradient is even reversed. The absorption of UV radiation not only leads to heating, but also to the formation of ozone . A temperature gradient smaller than the adiabatic limit value also applies in general to the higher atmosphere, since the radiation equilibrium generally dominates here - because the radiation equilibrium does not exceed the adiabatic limit value as in the troposphere.
The potential temperature is used to compare temperature values measured at different locations and altitudes .
illustration
To understand why temperature changes with altitude, it helps to imagine a weather balloon rising . In this thought experiment it is then necessary to fill the balloon with air and (somewhat less realistically) to assume that its volume can be changed at will, i.e. the surface is not rigid and can expand and contract at will. It is therefore a sharply delimited parcel of air that, isolated from its surroundings, slowly gains height and expands adiabatically. On the ground, the air pressure acts on the balloon envelope and compresses it to a certain volume. With increasing altitude, however, the air pressure decreases and the balloon expands until its internal pressure corresponds to that of the surroundings. Although no heat was added or removed from the balloon , the temperature of the air in the balloon has now changed. How come Adiabatic means that although no heat is exchanged, the molecules still do volume work when they expand at the expense of their kinetic energy. This reduces the internal energy in the balloon by the amount that had to be applied to displace the surrounding air.
Let us consider the physical quantity temperature . One possibility of temperature measurement is based on the fact that the molecules transfer their kinetic energy to a measuring device by impact (as a result, e.g. the alcohol in the thermometer expands ). In addition to the individual feeling of each person for it, temperature is nothing more than a macroscopic measure for the mean kinetic energy of the atoms and molecules, which is part of the internal energy. In contrast to energy, temperature is an intense variable, i.e. independent of the amount of substance.
With the expansion of the balloon, the kinetic energy of the molecules has decreased; the temperature of the air in the balloon is measured lower.
On the other hand, if you consider an air parcel at constant height, which is exposed to a change in air pressure, then this leads to compression or expansion and thus always to a change in temperature, since the work done during the change in volume is offset by a change in the internal energy of the gas must become.
The changes in temperature and pressure can in turn affect the physical state of the constituents of the air, because these only occur as gases under certain conditions. This can be seen with water vapor, because only it can condense into liquid water or resublimate into ice under atmospheric conditions. Since the heat that is released has an influence on the temperature, a distinction is made between dry and wet adiabatic temperature gradients.
Dry adiabatic temperature gradient
The dry adiabatic temperature gradient (abbreviation DALR for dry adiabatic lapse rate ) applies to adiabatically reversible and therefore isentropic conditions without any changes in the physical state . It is 9.76 Kelvin or degrees Celsius per one kilometer of altitude and is used to change the altitude of an air parcel as long as the relative humidity remains below 100 percent, i.e. the dew point is not exceeded and condensation does not occur. As a simplification, a gradient of one Kelvin per hundred meters is usually estimated. It is of great importance that this value, apart from small fluctuations due to differences in air composition and severity , is independent of altitude, i.e. the increase or decrease in temperature is linear.
The derivation of the gradient is based on the first law of thermodynamics (1.1) and the assumption of an ideal gas. The considerations are based on one mole .
|
|
|
(1.1)
|
|
|
|
|
|
(1.2)
|
|
|
Here, C m, V is the molar heat capacity of the air at constant volume. If the thermal equation of state of ideal gases is included in differential form (2.2), the expression (2.3) is obtained after conversion and equation.
|
|
|
(2.1)
|
|
|
|
|
|
(2.2)
|
|
|
|
|
|
(2.3)
|
|
|
With the relation (3.1) one can replace the molar heat capacity at constant pressure C m, p by the molar heat capacity at constant volume C m, V , and with the help of the general gas equation (3.2) the volume is eliminated and one obtains (3.3) .
|
|
|
(3.1)
|
|
|
|
|
|
(3.2)
|
|
|
|
|
|
(3.3)
|
|
|
For adiabatic processes, d Q = 0 applies , which further simplifies the equation and, with a small adjustment, leads to equation (3.4).
|
|
|
(3.4)
|
|
|
This equation can now be equated with the barometric altitude formula (4.1), where d h stands for the change in altitude. Shortening and reshaping gives equation (4.2).
|
|
|
(4.1)
|
|
|
|
|
|
(4.2)
|
|
|
Solving equation (4.2) for the temperature gradient d T / d h = Γ results in
|
|
|
(4.3)
|
|
|
If the specific heat capacity of the air at constant pressure c p = 1.005 J / (g K) and the acceleration due to gravity g = 9.81 m / s² are used, the value of −9.76 K is obtained for the dry adiabatic temperature gradient Γ / km.
The above values are those of dry air , so the quite variable proportion of water vapor with slightly different material values is usually neglected. If it is included in the form of a specific humidity of 0.01, which is a fairly typical value that can be taken as an average, the temperature gradient is 0.86% lower. Provided that no condensation occurs, the influence of the water vapor is therefore quite small.
A variant of the derivation is based on the adiabatic equation .
The logarithmic form is differentiated:
With
from the barometric altitude formula one obtains
M = 0.02896 kg / mol is the molar mass of the air, g = 9.806 m s −2 the acceleration due to gravity at the 45th parallel and R = 8.314 J mol −1 K −1 the universal gas constant. The value 1.4 for the adiabatic exponent takes into account that vibrations in the air molecules are not stimulated to any significant degree. With this, the temperature gradient of the dry adiabats, as in equation (4.3)
Moist adiabatic temperature gradient
For the feuchtadiabatischen temperature gradient (abbreviation Malr or SALR to English. Moist or saturated adiabatic lapse rate ) likewise apply adiabatic conditions, but explicitly in the event that a condensation of water vapor occurs. The condensation heat ( latent heat ) of 2257 kJ / kg contained in the gaseous state of aggregation is released and increases the sensible heat energy of the air. The dry adiabatic temperature gradient is weakened by this additional energy supply. How strong this attenuation of the DALR is depends on the temperature, because the higher it is, the greater the rise in the saturation vapor pressure curve and the more water vapor condenses per Kelvin cooling, i.e. H. the more sensible heat energy is released per Kelvin cooling. At high temperatures it can therefore be less than 4 K / km, but at a temperature of −40 ° C it can be 9 K / km very close to the dry adiabatic gradient. The figure on the right shows an idealized temperature profile with a constant gradient of 6.5 K / km, which corresponds to the Central European average.
Ambient gradient
The ambient gradient , usually referred to as the geometric temperature gradient , represents the actual temperature profile of the atmosphere, as it can be measured by radiosondes . Due to a large number of diabatic , advective and convective processes, it can deviate considerably from the model conceptions of a dry or wet adiabatic gradient and can also vary significantly around its own mean value. A gradient that is greater than the dry adiabatic is referred to as over-adiabatic and, accordingly, a lower gradient as under-adiabatic. Γ is used as the symbol for the negative geometric gradient with a consequent positive numerical value .
If one looks at the entire troposphere, there are often completely different gradients at different heights, with a sequence that is characteristic of the respective weather situation . A reversal of the gradient in the form of an inversion is also possible. The stratification stability of the earth's atmosphere is derived from the density differences that result in an air package that is adiabatically heated or cooled via dynamic gradients .
literature
- Walter Roedel: Physics of our environment. The atmosphere. 3rd, revised and updated edition. Springer, Berlin a. a. 2000, ISBN 3-540-67180-3 .
- Hans Häckel : Meteorology (= UTB for science. Uni pocket books 1338). 4th, completely revised and redesigned edition. Ulmer, Stuttgart (Hohenheim) 1999, ISBN 3-8252-1338-2 .