dew point
The dew point , the dew point is in the air with a certain humidity that temperature which are below at constant pressure has to allow water vapor as dew or fog can deposit. At the dew point, the relative humidity is 100% and the air is (just) saturated with water vapor . The more water vapor the air contains, the higher its dew point temperature. The dew point can therefore be used to determine the absolute humidity . The dew point is measured directly with a dew point mirror hygrometer or indirectly with other hygrometric methods. The term dew point is also applied to other gas mixtures with condensable components. The Greek letter is often used as a symbol for the dew point temperature .
Physical background
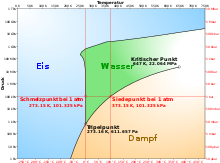
The dew point describes the temperature of a moist gas mixture in a state of equilibrium in which the condensation and evaporation of the moist component are exactly in balance. The gas is then just saturated with the steam . The moist gas mixture is usually a mixture of water vapor and air, but it can also refer to another mixture with a condensable component. The vapor partial pressure that prevails at the dew point is the saturation vapor pressure . How high the saturation vapor pressure is at a given temperature results from the phase diagram of the water or the condensable component of the gas mixture in question. Since the non-condensable components have almost no effect on the behavior of the steam, the dew point of moist air does not depend on the total pressure, but almost exclusively on the partial pressure of the water vapor contained. Each such state of equilibrium is determined by a point in the pT diagram. If you connect all these points with each other, you get the dew point curve as a phase boundary line . In some specialist books, the term dew point is not used for the temperature alone, but for the state of saturation, the associated temperature is then called the dew point temperature .
Below the triple point in the phase diagram , the gaseous state of aggregation does not change into the liquid, but into the solid. So frost forms and one speaks here of the frost point instead of the dew point. Here there is a dynamic equilibrium between solid and vapor phase, so that sublimation and resublimation are exactly in balance.
In the phase diagram, the state of an air-vapor mixture without a liquid phase is below or to the right of the dew point curve (e.g. at the red point in the figure). Then the horizontal distance to the dew point curve shows the temperature difference to the dew point at the same pressure. It is called the dew point difference or spread . The dew point difference is an important variable when predicting thermal and cloud base . The dew point difference is large in dry air and small in moist air. In the vertical direction, i.e. H. at the temperature of the red point, its height, expressed as a percentage of the height of the dew point curve, shows the relative humidity , i.e. the current vapor partial pressure compared to the saturation vapor pressure. In order to condense the steam from a relative humidity below 100%, a point on the dew point curve must be reached. B. the system can be cooled at constant pressure or volume until the dew point temperature is reached. Another possibility is to reduce the volume, because this increases the steam partial pressure in the opposite proportion. The point at which the dew point curve is reached depends on the isothermal or non-isothermal process control during the compression. In any case, the relative humidity increases to 100%.
Measurement
A direct measurement of the dew point can be made with a dew point mirror hygrometer. This contains a temperature-controlled mirror . If the mirror reaches or falls below the dew point temperature as the mirror temperature drops, it will fog up. This changes its optical properties, especially its reflectivity . In this way, measuring optics determine the dew point.
An indirect method combines the measurement of the room temperature with that of the relative humidity . The absolute humidity is calculated from these two data and from this the temperature can be determined at which the relative humidity reaches the value of 100%. In modern measuring devices, this calculation is carried out internally by a microprocessor ; the measured room temperature, the relative humidity and the dew point temperature are usually displayed.
Usage examples
meteorology
In meteorology , the dew point is used as a measure of air humidity. If the respective air temperature corresponds to the dew point, the relative humidity is 100%. The term sultriness can be defined using the dew point: Sultry is felt when the dew point exceeds approx. 16 ° C.
If the temperature of the air falls below its dew point, which is often the case in the early morning hours with air close to the ground, some of the water vapor liquefies: dew or fog forms, and frost at lower temperatures . It is sufficient if individual objects, for example cars, cool down below the dew point through heat radiation . Moist air passing by then also cools the surface of the objects to below the dew point and the windows mist up with condensation or ice flowers . If the temperature rises above the dew point, this precipitation dissolves again.
Similar processes are also responsible for the formation and dissolution of clouds: heated air masses rise from the ground and cool down by approx. 1 ° C per 100 m. One speaks of the " dry adiabatic temperature gradient ". Initially, the amount of water vapor contained in the air package remains unchanged. At a certain altitude, the temperature of the air mass reaches the dew point. This is where condensation sets in and a cumulus cloud forms. The cloud base is exactly at this height. If the air rises further, the temperature decreases more slowly because condensation heat is released (see moisture adiabatic temperature gradient ). In order to be able to assess the development of the clouds, vertical profiles of the temperature and the dew point are regularly created with the help of radiosondes . This information about the stratification of the atmosphere can be used to predict thunderstorms, for example.
Building physics
In the case of building materials that are permeable to water vapor and permeable to diffusion , water vapor diffuses through the component due to the concentration gradient. Where in the wall the material temperature is lower than the dew point, the water vapor condenses and wets the component. This occurs mainly in winter on above-ground floors and in summer in cellars or earthworks. The amount of condensation that has accumulated has to dry out again over the year, otherwise there is a risk of structural damage. The Glaser method is used to calculate or graphically determine the amount of condensation . As Taupunktebene the surface is referred to which the temperature corresponding to the dew point of water vapor. The moisture transport can be reduced by a vapor barrier .
If the surface temperature of external components is below the dew point, this leads to the formation of superficial condensation and consequently to the formation of mold. With an interior temperature of 18 ° C and a relative humidity of 40%, the dew point is around 4 ° C. If the internal temperature is 22 ° C and the humidity is 70%, the dew point is approx. 16 ° C. A surface temperature of 10–12 ° C is often assumed as the average value in living spaces.
In poorly insulating windows, the room air cools below the dew point and moisture steams up the glass. At temperatures below the frost point, ice flowers form on the window pane.
If good heat-insulating glazing and exterior doors are installed, the window frames and door frames often represent the coldest spots in the room. In order to avoid the formation of condensation and mold in winter, a surface temperature below the dew point of the room air should be avoided, as everywhere.
Dehumidification
With the help of condensation dryers , moisture can be separated from room air. The air temperature must be well above freezing point. The room air is cooled down to below the dew point in a heat exchanger, the condensable humidity runs off, then the air dehumidified in this way is heated again via a heat recovery register. The functional principle is also used in the tumble dryer .
As a side effect, heat is introduced into the room. On the one hand, by converting the electrical energy used to operate the refrigeration machine and fan into waste heat and by releasing the heat of condensation from the phase transformation of the water. In addition, there is a certain amount of air circulation and mixing.
Pneumatics
If a moist gas mixture is compressed, the vapor partial pressure and thus the dew point temperature rise as well. The water vapor then condenses at higher temperatures. In pneumatics , the compressed air is therefore dried before use, e.g. B. with refrigeration dryers . This means that the compressed air can also be used at low temperatures without water condensing in the pressure lines or transport containers or freezing water clogging the lines.
Dew points for other gas mixtures
In the case of multi-component systems (for example exhaust gases , distillation mixtures , natural gas) , a dew point range can be specified , analogous to the boiling range or condensation range .
The hydrocarbon dew point describes the dew point of a hydrocarbon mixture, whereby the dew points of the individual hydrocarbon components are taken into account in physical separation processes . Especially in a gas mixture, the dew point is then Erdgastaupunkt mentioned. In practice, the hydrocarbon dew point is also calculated indirectly from a gas chromatographic analysis, but this is fraught with major errors.
The dew point temperature of condensable components in the exhaust gas is referred to as flue gas dew point designated in flue gases than Rauchgastaupunkt . Avoidance of falling below the dew point in the flue gas prevents sooting of a chimney , however, when using the calorific value, falling below the dew point is desirable in order to use the latent heat present in the flue gas . The dew point of acids in flue gas is called the acid dew point . The sulfuric acid dew point specifically describes the dew point for sulfuric acid in flue gases. To distinguish it from these, the dew point of water vapor in smoke and exhaust gases is referred to as the water vapor dew point .
Calculation of the dew point of moist air
Abbreviations
The following terms are used:
| Mass of the water or the water vapor or the dry air in kg | |
| Water content in kg / kg | |
| Temperature in Kelvin or in ° C | |
| Dew point temperature in ° C | |
| Pressure of the humid air in hPa | |
| Partial pressure of the steam or dry air in hPa | |
| Saturation vapor pressure in hPa | |
| relative humidity | |
| universal gas constant | |
| molar mass |
Fundamental connections
The water content is the ratio between the mass of water contained in the mixture and the mass of dry air .
In the unsaturated state, all of the water is available as steam. One can write for it:
The partial pressures of the steam and the dry air describe the state of the mixture components. The sum of the partial pressures is the barometric pressure of the moist air.
The partial pressure is the pressure that the respective mixture component would assume if it were to fill the mixture volume alone at the same temperature . The thermal equation of state for ideal gases can be formulated:
The ratio of the molar masses of water to dry air is 0.622.
Equation (3) can be used to formulate the partial pressure of the steam
The relative humidity is the ratio of the partial pressure of the vapor to its saturation vapor pressure .
From equation (7) can be derived
Saturation vapor pressure
The dependence of the saturation vapor pressure on water is known from measurements and is shown in tables and formulated in approximate equations. One possibility for describing the saturation vapor pressure is the Magnus formula , which has the following form:
The
parameters apply to
the saturation vapor pressure above water
in the temperature range
(below 0 ° C for supercooled water ).
The
parameters apply to
the saturation vapor pressure above ice
in the temperature range .
Dependence of the dew point temperature on the water content and barometric pressure
At the dew point, the steam is at saturation pressure. Equation (7) can be equated with the saturation pressure of the dew point temperature.
Depending on which formulation is used for the temperature dependence of the saturation vapor pressure, an iterative solution or an explicit formulation for the dew point temperature can be found. By inserting the Magnus formula (10), equation (11) can be converted according to the dew point temperature .
The validity of these approximations is limited to the temperature range that already applies to Magnus' formula (10).
Dependence of the dew point temperature on relative humidity and air temperature
At the dew point, the relative humidity is equal to 1 (= 100%)
Dividing equation (9) by equation (13) results in
After inserting the Magnus formula, the relationship can be reformulated
The validity of these approximations is limited to the temperature range that already applies to Magnus' formula (10).
Web links
- Stefanie Lorenz, Hilke Stümpel: Learning module "Condensation and humidity measurements". Water in the atmosphere. In: WEBGEO basics / climatology. Institute for Physical Geography (IPG) at the University of Freiburg , October 1, 2001, accessed on December 14, 2010 . (requires Flash)
Individual evidence
- ↑ Ernst Lecher: Textbook of Physics for Doctors, Biologists and Psychologists, reprint of the original from 1921 . Salzwasser Verlag, Paderborn 1921, ISBN 978-3-8460-3190-2 ( limited preview in the Google book search).
- ^ Dieter Meschede: Gerthsen Physics . Springer DE, January 1, 2010, ISBN 978-3-642-12894-3 , p. 310–.
- ↑ Douglas C. Giancoli: Physics: Teaching and practice book . Pearson Deutschland GmbH, 2010, ISBN 978-3-86894-023-7 , pp. 639-.
- ^ Paul Dobrinski, Gunter Krakau, Anselm Vogel: Physics for engineers . Springer DE, December 11, 2009, ISBN 978-3-8348-0580-5 , p. 209–.
- ↑ a b Katja Bammel, Angelika Fallert-Müller, Ulrich Kilian, Sabine Klonk: The Brockhaus Weather and Climate: Phenomena, Forecast, Climate Change . Brockhaus, Mannheim 2009, ISBN 978-3-7653-3381-1 . P. 306.
- ^ Herbert Windisch: Thermodynamics . 3. Edition. Oldenbourg, Munich 2008, ISBN 978-3-486-58276-5 ( limited preview in Google book search).
- ↑ Dieter Baehr, Stephan Kabelac: Thermodynamics . 15th edition. Springer, Berlin, Heidelberg 2012, ISBN 978-3-642-24160-4 ( limited preview in Google book search).
- ↑ Herwig Wakonigg: The sultriness in Styria . with extensive meteorological definitions. In: Communications of the natural science association for Styria . tape 105 , 1975, pp. 116 ( PDF file; 1.5 MB [accessed October 22, 2013]).
- ↑ Joseph Krauß: Basic features of maritime meteorology and oceanography, reprint of the original from 1917 . Salzwasser Verlag, Paderborn 2011, ISBN 978-3-86444-130-1 ( limited preview in the Google book search).
- ↑ Ulrich Schumann (Editor): Atmospheric Physics, Background - Methods - Trends . Springer, Berlin / Heidelberg 2012, ISBN 978-3-642-30182-7 ( limited preview in the Google book search).
- ↑ Vertical profiles at wetteronline.de
- ↑ dew point table at Holzfragen.de; accessed in November 2016
- ↑ Characteristic data of building envelope and heating load , data pool IfHK, FH Wolfenbüttel; accessed in November 2016
- ↑ Maco Transit - Wood catalog , information on the temperature at the intersection of the floor and the door threshold on page 7
- ↑ Christoph Lechner, Jörg Seume (editor): Stationary gas turbines . Springer, Berlin Heidelberg 2010, ISBN 978-3-540-92787-7 ( limited preview in the Google book search).
- ↑ Günter Cerbe: Fundamentals of Gas Technology . 7th edition. Hanser Verlag, Munich / Vienna 2008, ISBN 978-3-446-41352-8 ( limited preview in Google book search).
- ^ Lueger: Lexicon of technology. Volume 17, p. 223.
- ↑ Horst Malberg: Meteorology and Climatology . Springer, 2002, ISBN 3-540-42919-0 ( limited preview in Google book search).
- ^ Dietrich Sonntag: Advancements in the field of hygrometry (Meteorol. Zeitschrift, NF 3) . Borntraeger brothers, Berlin, Stuttgart April 1994, p. 51-66 .