First law of thermodynamics
The first law of thermodynamics describes the conservation of energy in thermodynamic systems. It says that the energy of a closed system is constant. The energy balance can be calculated based on this statement: In a closed system, the sum of the internal and external energy is the sum of the work and heat performed on the system or taken from the system. In the open system, volume work and energies supplied or removed with mass flows must also be considered. With stationary processes and cycle processes , the energy balance is simplified because there is no change in the state variables over time.
Energy balance for the closed system
The first law of thermodynamics is derived from the law of conservation of energy : Every system has an internal energy , an extensive state variable . This can only change through the transport of energy in the form of work and / or heat across the boundary of the system. The following applies:
- It is the sum of the volume of work and the system dissipated work (eg., Friction work) indicates incomplete differentials , while full differentials features.
The equation applies to the system at rest. With the moving system, the external energies (potential and kinetic energy) are added:
The energy of a closed system remains unchanged. Different forms of energy can transform into one another, but energy can neither be generated from nothing nor can it be destroyed. Therefore a perpetual motion machine of the first kind is impossible (no system does work without supplying another form of energy and / or without reducing its internal energy).
A limitation of the convertibility of heat into work results from the second law of thermodynamics .
Energy balance for any open system
Applied to the open system, the first main clause is formulated differently mathematically. In the open system, in addition to the mechanical work on the displaceable system limit (volume change work e.g. on the piston in a cylinder), the displacement work of the mass flows at the inlet and outlet flow beyond the specific system limit. They are the product of pressure and volume. Instead of the internal energy, the open system therefore uses the enthalpies that contain this term. It is: resp.
The balance equation for an unsteady system in which both the mass content and the energy content change over time is:
Where:
- the change in the internal energy of the system over time.
- the heat flow over the system boundary.
- the work flow ( technical work ) beyond the system boundary.
- the mass flow into the system.
- the mass flow from the system.
- the specific enthalpy.
- the specific potential energy (with = height above the reference level and = acceleration due to gravity).
- the specific kinetic energy (with = speed).
Special cases and simplifications
- Closed system: (see above)
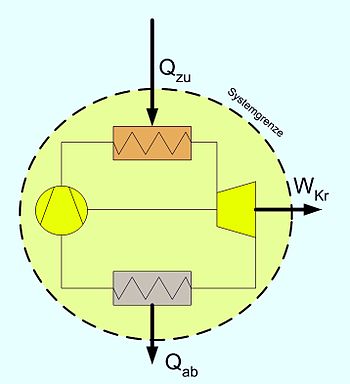
- Stationary process: and (see adjacent picture)
- or:
- additionally adiabatic (e.g. steam turbine):
- Here P is the shaft power of the machine. Since energies released by the system are defined negatively in thermodynamics, the power of a turbine from this equation becomes negative. In practice, the sign is therefore changed. In simplified calculations one also neglects the external energies. With known states at the inlet and outlet, the specific power can then be read off directly from the hs diagram as the difference in ordinates .
Energy balance for circular processes
Since the working medium returns to its initial state after running through a cycle, the balance is simplified. There are no changes in the state variables over time and the process variables heat and work remain. According to the second law of thermodynamics , not only can heat be supplied that is completely converted into work, but heat must also be removed. The simple balance equation is:
The circle integral adds up all heat flows. They are positive when they enter the system and negative when they leave. is the entire work of the cycle. It is negative when given away.
The relationship is also often written with the amounts of heat:
- ,
whereby the heat dissipation becomes more clearly recognizable.
Finally, the thermal efficiency of an engine should also be
still be mentioned, which sets the benefit (the cycle work) in relation to the expenditure (the supplied heat, which usually has to be generated in the form of fuel). In technical implementations, the dissipated heat is usually absorbed by the environment.
See also
- Nernst Theorem (Third Law of Thermodynamics)
literature
-
Karl Stephan , Franz Mayinger: Thermodynamics. Basics and technical applications. 2 volumes, Springer Verlag
- Volume 1: One- component systems . 15th edition, 1998, ISBN 3-540-64250-1 .
- Volume 2: Multicomponent Systems and Chemical Reactions . 14th edition, 1999, ISBN 3-540-64481-4 .
- Hans D. Baehr, S. Kabelac: Thermodynamics, Fundamentals and Technical Applications 13., revised. u. exp. Ed., Springer Verlag, 2006, ISBN 3-540-32513-1 .
- Hans D. Baehr, Karl Stephan: Heat and mass transfer 5., revised. Ed., 2006, Springer Verlag, ISBN 3-540-32334-1 .
- Klaus Langeheinecke, Peter Jany, Eugen Sapper: Thermodynamics for Engineers . 5th edition. Vieweg Verlag, Wiesbaden 2004, ISBN 3-528-44785-0 .