Thermodynamic system
A thermodynamic system is a spatially delimitable object with physical properties that can be described by the laws of thermodynamics . It must be demarcated from its environment, but not isolated. What is to be added to it must be clearly and unambiguously ascertainable based on the definition. The definition of the boundary surfaces to the environment, also called system boundaries , is arbitrary; A clever choice of the system boundaries can considerably simplify the solution of a thermodynamic problem.
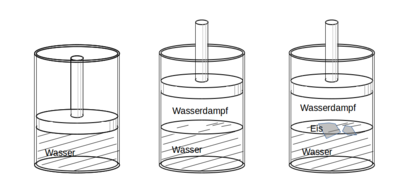
An example of a thermodynamic system is a piece of ice floating on water. A lot of seawater in a beaker can also be viewed as a thermodynamic system; the salt dissolved in the sea water, on the other hand, is not a thermodynamic system. Further examples of thermodynamic systems are the contents of a sealed bottle of mineral water, the contents of a thermos flask, the air in the piston of an air pump or the mixture in the combustion chamber of a furnace or an internal combustion engine.
A thermodynamic system does not need to be isolated from its environment. The piece of ice floating on the water can both release water molecules and energy to its surroundings of water and air, as well as absorb from it. A system that can exchange both matter and energy with its environment is called open ; a system that can exchange energy but no matter with its environment is called closed ; and a system that cannot exchange energy or matter is called closed or isolated . In the above examples, the piece of ice and the seawater in the beaker are open systems, the closed mineral water bottle is a closed system and the contents of the vacuum jug are approximately an isolated system.
The different states of equilibrium of thermodynamic systems and the energy and material conversions when changing from one state of equilibrium to another are the subject of thermodynamics.
General
Thermodynamic systems were first considered in the search for an optimal heat engine. Nicolas Léonard Sadi Carnot called them “substance employée” and “substance mise en œuvre” in his famous work of 1824. Rudolf Clausius wrote of an “effective body” in 1850, and Josiah Willard Gibbs used the term “material system” in his analysis of heterogeneous systems ". Towards the end of the 19th century the term “thermodynamic system” was established.
A thermodynamic system is a physical object that can be described in the context of thermodynamics by a mathematical model. The postulates of thermodynamics and specific material constants allow conclusions to be drawn from this model about the physical and chemical properties of the system for various environmental conditions and external influences.
In addition, hypothetical thermodynamic systems are considered in some thought experiments ; For example, systems with partitions that only allow certain atoms or molecules to pass, although such selective partitions are not known for every arbitrary molecule. In thought experiments on cavity radiation, containers with ideally reflective inner walls are used. They contain no matter, just electromagnetic fields. With such a cleverly thought-out, hypothetical “mirror box” as a thermodynamic system, Willy Wien was able to theoretically justify the law of displacement for cavity radiation in 1893 .
Equilibrium and variables of state
A thermodynamic system is in equilibrium when the directly ascertainable properties and other measurable quantities known from previous theories - such as distances, mass values, forces - do not change over time; with Vortheorien mostly mechanics and electrodynamics are meant. The theory of the equilibrium states of thermodynamic systems is called thermostatics .
In the mathematical model of a thermodynamic system, some parts of the system are replaced by idealized constraints. The system boundaries are viewed as idealized edge areas; Size and shape are externally predetermined conditions. These idealized constraints are taken into account by one or a few parameters in the model. These parameters are called work coordinates or external state variables . With systems in a single container, there is often only one working coordinate, namely the volume of the container. In the case of objects, such as a drop of water, for which surface tension plays a role, the size of the surface is also a working coordinate. If the system is in a homogeneous external magnetic field, then the magnetic dipole moment of the entire system is another working coordinate.
The set of possible equilibrium states of a thermodynamic system corresponds in the mathematical picture to an area in a finite dimensional real vector space , it is the state space of the equilibrium states . The working coordinates can be used as coordinates for specifying a state, but they alone are not sufficient to clearly define a state of equilibrium of a thermodynamic system. For this purpose, the values of internal state variables (such as internal energy or temperature) must also be specified.
Simple thermodynamic systems
Thermodynamic systems whose states of equilibrium are uniquely determined by a set of working coordinates and the specification of the internal energy are called simple thermodynamic systems . Most of the systems considered in textbooks and in engineering thermodynamics are simple thermodynamic systems. According to Lieb and Yngvason, the simple thermodynamic systems are the building blocks of thermodynamics.
Examples of simple thermodynamic systems are:
- One mole of water in one flask (one working coordinate)
- Half a mole of oxygen in a flask in a homogeneous magnetic field (two working coordinates: volume and magnetization)
- The systems of Examples 1 and 2 are connected by a thermally conductive copper wire (three working coordinates)
An example of a not simple thermodynamic system is an overall system consisting of two simple systems isolated from one another. Systems with ferromagnetic material in a magnetic field are also not simple thermodynamic systems because of their hysteresis.
Scalability
For scaling a thermodynamic system is defined: all geometric dimensions, so all distances by a factor and all the quantities by a factor multiplied, so are the state variables that it is a factor of change, extensively and those that are not thereby change, called intense . According to Ludwig, the working coordinates should be extensive state variables. Internal energy and entropy are also extensive quantities of state, while pressure and temperature are intense quantities of state.
The requirement that state quantities are extensive or intensive restricts the state quantities as functions of the coordinates over the state space. From this scalability, important relationships for the chemical potentials, such as the Gibbs-Duhem equation , can be inferred . For a simple thermodynamic system with a work coordinate , pure substances with the amounts of substance and the internal energy , if there is a state of equilibrium, then the point is also an equilibrium point for the system scaled by the factor .
If one divides an extensive state variable by the amount of substance, the mass or the volume of a substance, then one obtains an intensive, i.e. scale-invariant, variable which is referred to as molar state variable, specific state variable or density .
Classifications
According to the internal structure
Thermodynamic systems can be composed of different materials in a very complex manner. They can be classified according to their internal structure.
Areas of a thermodynamic system in which local physical properties such as density and pressure, as well as the chemical composition are the same everywhere, are called homogeneous according to Gibbs and assigned to a phase . For example, in a system made up of water and a few ice cubes, all ice cubes are assigned to a phase. The same chemical composition does not mean that there is only one single chemical substance, it can also be a mixture of different substances.
A thermodynamic system is called homogeneous if it only consists of a single phase, otherwise heterogeneous . Homogeneous thermodynamic systems consisting of only a few phases can be described with the methods of thermostatics with a finite dimensional state space,, .
Other more complex systems require a continuum theory within the framework of irreversible thermodynamics. In this theory, local equilibrium states and spatially and temporally varying state variables are introduced. The state variables are fields that have to satisfy a set of partial differential equations; Examples of this are the thermal conduction equation for solids and the Navier-Stokes equations for liquid or gaseous systems. If force fields such as electromagnetic fields or the gravitational field play a role, this leads to inhomogeneities in spatially extended systems; one example is the system of the earth's atmosphere in meteorology, another the interiors of stars in astrophysics. In many technical thermodynamics textbooks, such systems are excluded in advance. In the physical literature, too, thermodynamic systems are usually only spoken of in connection with systems in thermostatics consisting of a few phases. The technical textbooks deal primarily with systems that only consist of gaseous or liquid phases. One speaks of a fluid and means a liquid or a gas.
According to fabric components
Furthermore, the thermodynamic systems can be classified according to the number of pure substances (chemical compounds or chemical elements) inside. An understanding of the thermodynamic properties of systems that consist of only one single substance is often a prerequisite for the analysis of systems with mixtures . For systems consisting of only one pure substance, the equations of state for the thermodynamic state variables are usually available in graphics, tables or databases . Systems made from a single pure substance can be heterogeneous, namely when they consist of several phases; such as gaseous, liquid or various solid forms. If a liquid and a gaseous phase are present at the same time, one speaks of the wet steam area of the substance.
If a phase of a thermodynamic system contains a mixture of several pure substances, the phase is called a mixed phase ; this mixture is homogeneous as one phase. The mole fractions of the individual pure substances in a mixed phase are then additional state variables of the overall system. In the case of special applications, for example at very low temperatures, the isotopes of an element must also be treated as different pure substances, as with 3 He and 4 He .
There are mixtures in which the contained substances can react chemically. Thermodynamic systems with chemically reacting mixtures are only in thermodynamic equilibrium if a chemical equilibrium has also formed between the reactants and products . This chemical equilibrium depends on the thermodynamic parameters such as pressure and temperature. The analysis of such systems is central to physical chemistry and chemical process engineering .
After interaction with the environment
Thermodynamic systems can be classified according to their interaction with their environment; So according to whether energy and matter can pass the system boundaries:
A closed thermodynamic system does not interact with its environment; an isolated thermodynamic system is also used synonymously . Its place in the state space always remains at the same point after the equilibrium has been set. Isolated systems are of interest if the establishment of equilibrium is to be investigated. If one wants to know of two isolated thermodynamic systems which equilibrium is established when the two systems are connected or even combined, the overall system consisting of both individual systems should be isolated.
In closed thermodynamic systems, energy can only pass the system boundaries in the form of heat and work. If only the exchange in the form of work energy is possible, the system is called adiabatic .
In open systems, both energy and matter can cross the system boundary. Open systems are often found in technical systems. A turbine has two input streams (air and fuel), an output stream of combustion gases and an output of mechanical power via a shaft. In a rectification column, there is an incoming stream of a mixture and at least two outgoing streams with the enriched components of the mixture.
Balance equations
The system boundaries of an open system include a space that is often called the control room in technical applications ; the system boundaries are also referred to as the balance sheet . Balance equations for the energy and the amount of substance can be set up for such systems from the conservation laws for energy and matter .
Open system
In an open system, the system can exchange both energy and matter with its environment. An example of an open system in which a process takes place continuously is a turbine. In stationary operation, a constant mass flow flows through the system, the mass balance results in zero. The states of the fluid at the inlet and outlet remain constant and the fluid changes its state on its way through the system. The shaft work is fed into the system when it is compressed and released when it expands. It's called engineering work .
It is described by:
(Here is the change in the external energies. The definition of technical work is different in the literature. Different one understands only the first term ).
In addition to this work, shift work occurs at the entry and exit of the system . In stationary operation, if the mass particle has the same volume at the inlet and the same at the outlet , the work of displacement is at the inlet , correspondingly at the outlet
This shift work is contained in the respective enthalpies in addition to the internal energy . With the definition of enthalpy
is the balance for the open stationary system:
and with the symbol for the achievement
and the external energy
the first main clause for the application in the open system is:
The internal combustion engine shown in the sketch as an example of an open system is, strictly speaking, alternately open and closed. It can only be viewed as an open system over longer periods of time.
Closed system
In a closed system, energy can be added or removed in the form of heat, radiation and work. The following work can be considered:
- The reversibly applied volume change work , called volume work. Example in the sketch: The piston compresses the gas in the cylinder without friction. Since is negative, the work done is positive.
- Dissipated work . An example is a fan or an electric heater in a room with a rigid system boundary. Work ( exergy ) flows across the system boundary and is dissipated within the system. The work by frictional forces between piston and cylinder is one of these irreversibly supplied energies.
Since, according to the first law of thermodynamics, energy can neither be generated nor destroyed, the internal energy increases by the supplied energies. The balance for the closed system at rest is:
With
(The indices 1 and 2 designate the initial and final state, the index 1,2 the path from 1 to 2)
If the external energies of the system, i.e. the potential energy and / or the kinetic energy of the system, are changed by the influence of the supplied energies, the balance according to the 1st law for the closed system is:
Remarks
- ↑ According to Ludwig, temperature is only defined in the context of thermodynamics and should therefore not be used for the definition of the basic concept of thermodynamic equilibrium. Ludwig points out another difficulty in determining the state of equilibrium. For all known states of equilibrium there are always more refined measurements, the measurement results of which change (think, for example, of measuring the pressure using very small areas in very short time intervals). The area of application must therefore be limited to certain sizes. This restriction is often expressed by the short term thermodynamic observables for the permitted measurands. Which sizes these are is not determined from the start, but the area of application is only revealed through the application of the theory.
- ↑ Baehr and Kabelac also count the speed of the system in relation to its observer to the external state variables.
literature
- Hans Dieter Baehr, Stephan Kabelac : Thermodynamics - Basics and technical applications . 16th edition. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4 .
- Günther Ludwig : Introduction to the basics of theoretical physics . tape 4 . Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3 , XIV Thermodynamik, p. 5-145 .
Web links
Individual evidence
- ↑ a b c d Günther Ludwig: Introduction to the basics of theoretical physics . tape 4 . Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3 , XIV § 1. Thermostatics 1.1 The state space, p. 6-11 .
- ↑ a b c d e f Hans Dieter Baehr, Stephan Kabelac : Thermodynamics - Fundamentals and technical applications . 16th edition. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4 , 1.2 System and condition, p. 14-23 .
- ↑ a b c Gerd Wedler , Hans-Joachim Freund : Textbook of physical chemistry . 6th edition. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0 , 1.1.2 System and environment, p. 1-2 .
- ↑ a b c d e André Thess: The entropy principle - thermodynamics for dissatisfied . Oldenbourg Wissenschaftsverlag, Munich 2014, ISBN 978-3-486-76045-3 , 2.1 Thermodynamic Systems, p. 7 .
- ^ Nicolas Léonard Sadi Carnot: Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance . In: Annales scientifiques de l'École Normale Supérieure Sér. tape 2 , no. 1 , 1872, p. 393–457 (French, numdam.org [accessed April 14, 2018] reprint of work from 1824).
- ↑ Rudolf Clausius: About the moving force of heat and the laws which can be derived from it for the theory of heat itself . In: Annals of Physics and Chemistry . tape 155 , no. 1 , 1850, p. 368 ( archive.org ).
- ^ A b Josiah Willard Gibbs : On the Equilibrium of Heterogeneous Substances . In: Transactions of the Connecticut Academy of Arts and Sciences . tape 3 , no. V , 1878, p. 108–248 (English, biodiversitylibrary.org [accessed April 27, 2017]).
- ↑ Willy Wien: A new relationship between black body radiation and the second law of heat theory . In: Session reports of the Royal Prussian Academy of Sciences in Berlin . First half volume 1893, 1893, p. 55 ( bbaw.de [accessed on April 27, 2017]).
- ^ A b Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics . In: Physics Reports . tape 310 , no. 1 , 1999, II. Adiabatic accessibility and construction on entropy (A 1. System and their state spaces), p. 12-16 , doi : 10.1016 / S0370-1573 (98) 00082-9 , arxiv : cond-mat / 9708200 (English).
- ↑ Gerd Wedler , Hans-Joachim Freund : Textbook of Physical Chemistry . 6th edition. Wiley-VCH, Weinheim 2012, ISBN 978-3-527-32909-0 , 2.7 Interfacial equilibria, pp. 443-482 .
- ^ Walter Roedel: Physics of our environment. The atmosphere. 3. Edition. Springer Vieweg, Berlin 2000, ISBN 3-540-67180-3 , 5.1.1 The homogeneous condensation, p. 177-184 .
- ^ A b Günther Ludwig: Introduction to the basics of theoretical physics . tape 4 . Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3 , XIV § 1. Thermostatics 1.2 The energy law, p. 22 .
- ^ A b Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics . In: Physics Reports . tape 310 , no. 1 , 1999, III. Simple Systems, p. 36-42 , doi : 10.1016 / S0370-1573 (98) 00082-9 , arxiv : cond-mat / 9708200 (English).
- ↑ Constantin Carathéodory : Investigations on the fundamentals of thermodynamics . In: Mathematical Annals . tape 67 , no. 3 , 1909, pp. 355–386 ( digizeitschriften.de [accessed April 27, 2017]).
- ↑ Günther Ludwig: Introduction to the basics of theoretical physics . tape 4 . Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3 , XIV § 1. Thermostatics 1.2 The energy law, p. 27-28 .
- ↑ Günther Ludwig: Introduction to the basics of theoretical physics . tape 4 . Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3 , XIV § 2 Irreversible Processes, p. 84–145 (In particular §2.6 Heat conduction, §2.7 The Navier-Stokes equations, §2.8 Materials in the electromagnetic field).
- ^ Hans Dieter Baehr, Stephan Kabelac: Thermodynamics - Basics and technical applications . 16th edition. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4 , 4. The thermodynamic properties of pure fluids, p. 171-230 .
- ^ Hans Dieter Baehr, Stephan Kabelac: Thermodynamics - Basics and technical applications . 16th edition. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4 , 5. Mixtures and chemical reactions, p. 231-374 .
- ^ Hans Dieter Baehr, Stephan Kabelac: Thermodynamics - Basics and technical applications . 16th edition. Springer Vieweg, Braunschweig 2016, ISBN 978-3-662-49567-4 , 2.3 The energy balance equations, p. 66-88 .