barometer


A barometer ( ancient Greek : βαρύς barýs "heavy, pressed" and μέτρον métron " measure , measure") is a measuring device for determining the static absolute air pressure and thus a special form of the manometer .
If it is used for meteorological purposes, it shows a virtual value that would correspond to the aerostatic air pressure at sea level. As a special case, it can be used indirectly for height measurement .
A further development of the barometer is the barograph , which records the development of air pressure over time in writing or electronically. Another further development of the barometer is the microbarometer , which is able to measure even tiny pressure differences.
etymology
The term "barometer" was introduced in 1665/1666 by the Irish naturalist Robert Boyle . It is derived from the Greek βάρος báros "heaviness, weight" and μετρεῖν metreín "measure".
History of the barometer
Georgius Agricola mentions air pressure as the cause of the water rising in suction pumps.
Basics

At the time of Galileo , around 1635, the engineers and well builders of Florence were commissioned to build extensive irrigation systems in the gardens of the palace. They installed suction pumps , but were astonished to find that they were unable to draw water up to a height of about 10 meters. Galileo was called in and described the problem in his Discorsi e dimostrazioni matematiche in 1638 , but he died in 1642 without having had the opportunity to work out a solution to this problem. Galileo corresponded in 1630 with Giovanni Battista Baliani , who built a water barometer.
In his notes, dating back to 1614, we can read that although he thought about the weight of the air and determined it to be the 660th part of the weight of the water, he did not draw any further conclusions from this. The idea that the liquid was not drawn into the suction pump, but rather driven into it by the pressure of the air, contradicted the view at the time that the water rose because nature "disgusted the void" (lat. Horror vacui ) have.
Invention of the mercury barometer by Torricelli
Evangelista Torricelli followed Galileo as a physicist at the court of the Grand Duke of Tuscany after his death. He resumed his predecessor's studies and conducted experiments to prove that it was air pressure that kept the tube from emptying completely and that a certain column of mercury always remained. This was about 76 cm high, regardless of how far he dipped the pipe into the pool.
He concluded from this that the air pressure on the surface of the basin compensates for the weight of the mercury column related to the column area, and that analogously the water in the pumps can only be pumped up to about 10 meters if a vacuum is created with the pump. He also found that the mercury column changed over time and that a decrease in height preceded a period of bad weather. With this, Torricelli invented the barometer in 1643.
Since the open reservoir was extremely unsuitable for transporting the measuring instrument, various other solutions were considered. For example, leather porous reservoirs were made which were attached to the pipe and which contained a small amount of mercury.
Sir Robert Boyle bent the barometer tube upwards, resulting in a " siphon tube" as it is still used today.
The French physicist René Descartes (1596–1650) improved the Torricelli system by adding a paper scale. He is also the first to spread the idea that air pressure decreases with altitude.
Blaise Pascal and the air pressure
The air pressure causes a column of mercury to form about 76 centimeters high, but it is not enough to fill the vacuum above. Around 1640, the question of whether air has any weight was one of the most discussed topics among scientists.
Blaise Pascal was able to answer this controversial question in 1647 with his famous experiment vide dans le vide . Pascal also repeated Torricelli's experiment because, like Descartes, he was convinced that if the air had a weight, the mercury would have to rise less if the experiment were carried out at a higher altitude. This was also confirmed, albeit with very little accuracy, on the top of the 52 meter high tower of Saint-Jacques in Paris . With the help of his brother-in-law Florin Perrier , who lived at the foot of the Puy de Dôme , he repeated the experiment on September 19, 1648. He carried out the experiment at different heights and found that the height of the mercury column actually decreases with increasing sea level. In the following month, Pascal published his results in the treatise Récit de la grande expérience de l'équilibre des liqueurs .
Later the SI unit for the pressure was named after him as Pascal , which corresponds to one Newton per square meter .
Magdeburg hemispheres
Otto von Guericke was able to prove the air pressure with the Magdeburg hemispheres in 1663 and thus gained fame above all in Germany. These are two half hollow spheres lying close to one another, which could no longer be separated from each other even by teams of horses pulling in opposite directions, as soon as the spherical hollow body had been evacuated and evacuated . This is the principle that vacuum cabins still work today .
Later development
It was not until the middle of the 18th century that instrument manufacturers, opticians and watchmakers began producing barometers, initially for scientific purposes and then also for domestic use. From 1770 meteorological designations were added to the scales (good weather , changeable etc.).
In 1675 Abbot Picard, who was carrying a mercury barometer at night, made a curious discovery. With every movement a bluish light appeared from the pipe. This phenomenon has been studied by Francis Hauksbee , a student of Boyle's, but no satisfactory explanation has been found at the time. But from this point on, the first investigations into electrical discharges in highly diluted gases began. Today we know that it is the friction of mercury atoms on the glass wall that causes this light phenomenon.
Types
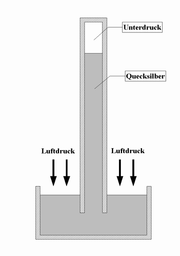
Liquid barometer
Liquid barometers consist of a vertical tube filled with a liquid , which is hermetically sealed at the top. The lower end is immersed in a storage vessel that also contains the respective liquid. The liquid flows out of the pipe due to its own weight, creating a negative pressure at the upper end . The air pressure counteracts this, so that the liquid column comes to rest at a certain height.
Mercury barometer
The most common use of mercury is the liquid, which is referred to as a mercury barometer . Under normal conditions , mercury reaches a height of 760 millimeters, so that the read value must be mathematically corrected to the standard conditions for exact results , whereby it should be noted that mercury and glass tube expand when the temperature increases :
With
- : Pressure
- : read pressure
- : Room temperature in ° C
- Expansion coefficient of mercury: 0.000181 / K
- For exact measurements, the geographical latitude and height must be taken into account.
- Relative height differences in the reservoir basin and pipe, due to their different cross-sections, are taken into account by a reading scale with “reduced graduation”.
Mercury is used because the tube can be kept short due to its high specific weight . For comparison, the pipe would have to be around 10 meters long in water . On the other hand, very little mercury evaporates , despite the vacuum at the upper end of the tube and the open lower end.
The first mercury barometer was invented by Evangelista Torricelli in 1643 . He observed that the height of the mercury column changed daily and concluded that the air pressure also changed accordingly. A unit for measuring air pressure (1 Torr = 1 mm Hg , corresponds to approx. 133.32 Pa ) was named after him.
Since 2009, the manufacture and sale of mercury barometers and other measuring devices that contain mercury in fragile containers has been banned in Germany as an implementation of an EU regulation.
Goethe barometer
General
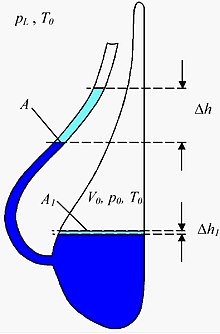
The principle of a liquid barometer is also used in a slightly modified form in a so-called Goethe barometer , which is also known as Goethe glass , Goethe weather glass , thunder glass or weather glass . This is a mostly decorative vessel filled with a liquid, the underside of which has a beak neck that is turned upwards and open to the earth's atmosphere , while the main vessel itself is closed off from atmospheric pressure. When the air pressure is low (or when the temperature rises), the liquid level in the beak neck rises and decreases accordingly when the air pressure is high. Although Goethe had such a barometer in his possession, he was not the inventor of this type of barometer. It is unclear when and by whom it was actually developed. But it should be as old as the appearance of glass vessels with spouts. Therefore, there are several earlier versions of the Goethe glass, including the Dutch thunder or weather glass, which was secured as early as 1619. The Goethe barometer, which is closed at the back, is preceded by carafe-shaped weather glasses with long, deep-seated spouts, which lasted into the 17th century. They still had to be sealed at the neck with a wax stopper.
Air pressure measurements with the Goethe barometer
Measurements of the absolute air pressure are not possible with the Goethe barometer, but changes in air pressure that occur within a few days can be measured. Since the enclosed air changes its volume even with temperature changes, the change in ambient temperature must be measured during the observation period. In addition, the cross-sectional area A of the beak and the volume of the trapped air must be determined. The change in air pressure that has occurred can then be calculated from the change in height of the liquid level using the following approximation formula ( water as liquid):
- G1:
Here only to be numerical values of physical quantities used, which, when using the units of the result of the following table:
| meaning | Unit for formula | typical values | |
|---|---|---|---|
| Temperature change since the start of the measurement | Degrees Celsius | -5 to +5 | |
| Cross-sectional area of the beak | cm² | 0.6 | |
| Volume of trapped air | cm³ | 100 | |
| Change in the height of the water column in the beak since the start of the measurement | cm | -5 to +5 | |
| Change in air pressure since the start of the measurement | hPa | −20 to +20 |
Equation G1 is based on the thermal equation of state of ideal gases , also known as the general gas equation, in the form:
If, in addition to the change in temperature of the gas, one also takes into account the change in volume of the enclosed air as a result of the change in the height of the liquid column in the beak, one obtains:
G2:
The following sizes also occur here:
is the ambient temperature at the beginning of the measurement. It can be used with 300 K without major errors. It still has to be measured because you need it.
is the location factor. It can be used with 10 N / kg.
is the density of water.
is the external air pressure at the beginning of the measurement. It can be set approximately the same .
is the pressure of gravity of the water column in the beak at the beginning of the measurement. He can be neglected towards .
is the size of the water surface in the vessel. The quotient can be neglected.
The quotient must not be neglected and must be determined as precisely as possible, otherwise you will get values that can be many times wrong.
If you put these values in G2 and if you want to use the values in cm, cm² and cm³ and get the result in hPa, this leads to equation G1.
Can barometer
With can barometers , also aneroid barometers (v. Greek : α-νηρός “a-nerós” “not liquid”), a can-like hollow body made of thin sheet metal is deformed by air pressure. There is a residual pressure of around 5 mbar (= 5 hPa = 500 Pa) in the can, which compensates for the change in the sheet metal's modulus of elasticity due to the temperature .
Such a hollow body is also called Vidie can after its inventor Lucien Vidie (1805–1866) . From 1881 Gotthilf Lufft was the first manufacturer of can barometers in Germany, who further developed the Vidie can and registered it as a patent in 1909.
Better barometers or barographs use a stack of up to eight such "cans" on top of each other to increase the sensitivity of the measurement. This deformation is transferred to a pointer via a mechanism, with increasing air pressure compression and with decreasing air pressure expansion . Vidie cans are also used in aviation for the altimeter , variometer and airspeed indicator . A pressure microphone also works according to this principle.
One problem is the temperature sensitivity of such a system: the components of the can show thermal expansion in volume . Therefore, special alloys are used for their construction , in which several components compensate each other according to their temperature behavior and thus reduce the disruptive effect of thermal expansion. Nevertheless, there are temperature- related measurement errors .
Tube barometer
The tube barometer ( Bourdon tube ) makes use of the fact that the outside of a bent tube has a larger area than the inside and thus the force from the outside is greater with increasing pressure. The deformation as a function of the pressure is transferred to a pointer.
Applications
Barometers are mostly used in meteorology and are a standard instrument for almost every weather station . Since air pressure decreases with altitude, they also serve as an altimeter in airplanes . If it is not the air pressure of the earth's atmosphere , but an artificially generated positive or negative pressure that is measured, one speaks of a manometer . Another related device is the variometer , which shows a change in altitude via the change in air pressure (see also hypsobarometer , altitude recorder and air pressure measurement in aviation ). The course of a change in air pressure is recorded with a barograph .
Often barometers, mostly of inferior quality, are used in the middle latitudes as "weather indicators ", as changes in air pressure and "bad" or "good" weather here partially influence each other. The reason for this is that the front penetration of dynamic low pressure areas results in a typical change in air pressure. Rising air pressure is interpreted as a sign of good weather and falling air pressure as a sign of bad weather. However, since these tendencies can only be justified meteorologically in certain cases and bad weather events can also be accompanied by rising air pressure, these only represent a very rough weather forecast .
However, the barometer was of great importance in shipping; because here the short-term weather forecast plays a bigger role. England was a leader in the development of marine barometers. Ship barometers worked according to the Torricellian principle, were about one meter high and were used in shipping until the 1860s. Compared to conventional, stationary barometers, they essentially had to meet two additional requirements: on the one hand, they had to withstand major vibrations. When cannons were fired (from one's own ship), the mercury columns broke regularly. The British Admiral Robert Fitzroy developed the so-called Gun Marine Barometer in the second half of the 19th century. It was distinguished by the fact that the mercury column was stored in soft rubber ("Indian Rubber"). From then on they no longer broke when the cannon was fired.
The second requirement for the ship's barometer was: it should remain vertical even when the ship is heeled (tilted position) so that the barometer can also be used. This affected not only the war navy, but also the merchant navy, including fishing. The problem was solved by gimbaling the ship's barometers. The cardanic now always ensured the same vertical position.
In combination with other measuring devices, barometers are used in aerographs .
For teaching purposes, a ten meter high water barometer has been set up at the Meteorological Institute of the Ludwig Maximilians University in Munich. The influence of the vapor pressure in the space above the water column can also be shown here.
A very interesting application of the canned aneroids is the automatic compensation of the influences of the fluctuating air pressure on precision pendulum clocks . The astronomer Professor Bernhard Wanach first proposed the use of a can barometer on pendulum rods in the 19th century. The arrangement of the so-called aneroid can compensation consists of several cans connected in series, which are loaded with a weight. The weight is moved by the cans depending on the air pressure along the pendulum rod and thus changes the moment of inertia of the pendulum . Even today excellent results are achieved with precisely calculated air pressure compensation instruments in precision pendulum clocks.
Figuratively
Because it is used for weather forecasting, other forecasting instruments are also known colloquially as "barometers". One speaks of stock market barometers (for predicting stock prices), election barometers (for predicting voting), etc.
literature
- FA Hegenberg: Lessons in measuring heights with the barometer according to the latest discoveries made in physics and belonging here . Appuns, Bunzlau 1828 digitized
- Johann Gottlieb Wiemann: Instructions for measuring altitude with the barometer . 2nd Edition. Arnold, Dresden [a. a.] 1828 digitized
See also
- Education barometer
- Barometer question
- Pascals Barometer , didactic piece of teaching art didactics
Web links
- The Barometer World Museum with over 100 historical barometers in Merton, Devon
- A collection of weather glasses also called Goethebarometer; further explanations on the history of the weather glass
- Basics of air pressure measurement with the Goethe barometer taking temperature changes into account (PDF; 265 kB)
Individual evidence
- ^ Georgius Agricola : De re metallica. Volume 6, ca.1550.
- ^ Christian Ucke, Hans-Joachim Schlichting: The Goethe Barometer. In: Physics in Our Time. Volume 24, 1993, pp. 91-92.
- ↑ Gotthilf Lufft, founder of Mech. Werkstätte G. Lufft, today G. Lufft Mess- und Regeltechnik .
- ↑ Website friends of old weather stations ( memento from June 1, 2014 in the Internet Archive ), source for the historical background of the company G. Lufft.
- ↑ Google Patents , source for patent application for aneroid barometer.
- ^ Negretti & Zambra: A Treatise on Meteorological Instruments . Ed .: Negretti & Zambra, London. 2nd Edition. Baros Books, Trowbridge, Trowbridge, Wiltshire 1995, ISBN 0-948382-09-0 , pp. 22 (first edition: 1884).
- ^ Philip R. Collins: Fitzroy and his barometers . Baros Books, Trowbridge, Wiltshire 2007, ISBN 978-0-948382-14-7 , pp. 40 .